初中数学沪科版（2024）七年级上册（2024）2.1 代数式图文ppt课件

这是一份初中数学沪科版（2024）七年级上册（2024）2.1 代数式图文ppt课件，共22页。PPT课件主要包含了πr2，x＋2y，a＋10b＋c，单项式，a2-a+7，项4a2-a7，常数项，次数是2，多项式的次数是2，次数是1等内容，欢迎下载使用。

1.能叙述并理解单项式及单项式的系数、次数的意义，能确定一个单项式的系数和次数.2.理解多项式、多项式的项和次数、整式的概念.3.会用整式解决简单的实际问题.
用代数式表示：（1）正方形边长为a，则周长为_____，面积为_____；（2）长为a，宽为 a的长方形的面积为______；（3）半径为r的圆的面积为______；（4）若m表示一个有理数，则它的相反数是______.
观察上述代数式，它们有什么特点？
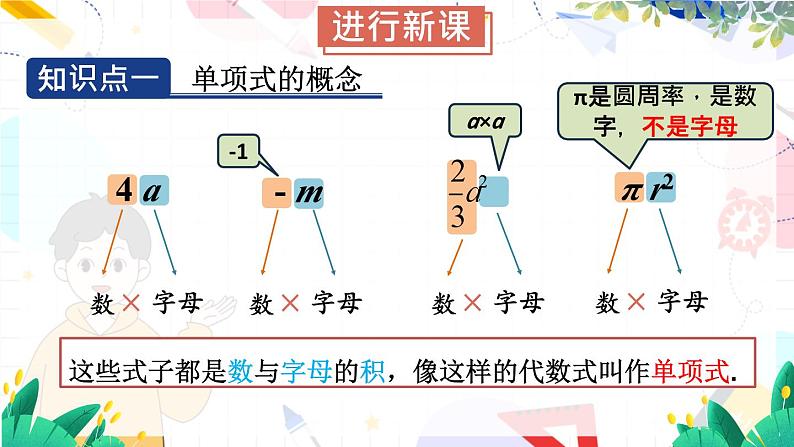
π是圆周率，是数字，不是字母
这些式子都是数与字母的积，像这样的代数式叫作单项式.
练一练：下列各式哪些是单项式？哪些不是单项式？
点拨：①单项式中只有乘除法，没有加减法;②单项式的分母中只含数，不含字母；③单个的字母或数也是单项式.
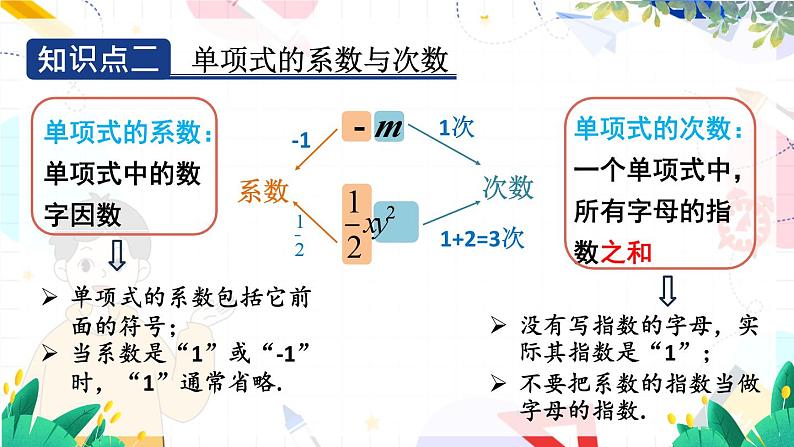
单项式的系数包括它前面的符号；当系数是“1”或“-1”时，“1”通常省略.
没有写指数的字母，实际其指数是“1”；不要把系数的指数当做字母的指数.
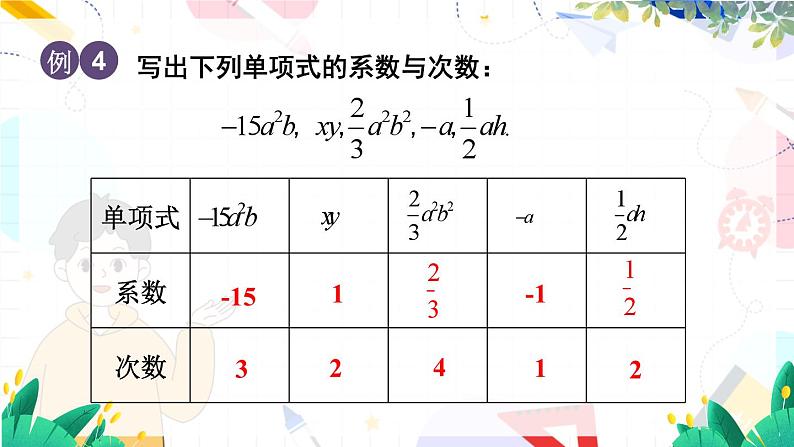
写出下列单项式的系数与次数：
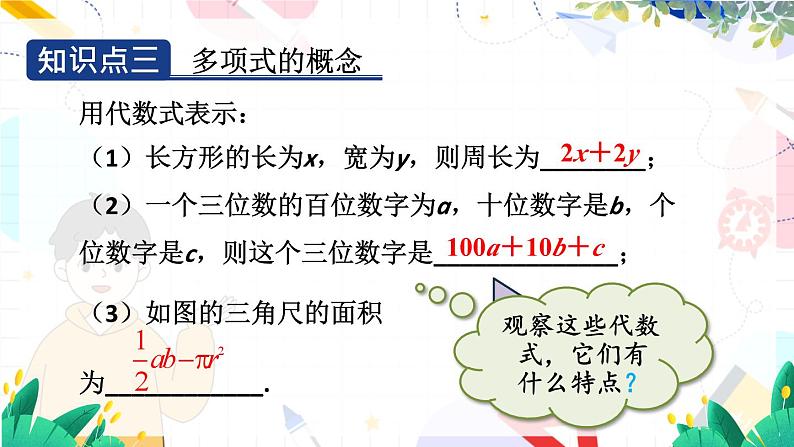
用代数式表示：（1）长方形的长为x，宽为y，则周长为________；（2）一个三位数的百位数字为a，十位数字是b，个位数字是c，则这个三位数字是______________；（3）如图的三角尺的面积为____________.
多项式：几个单项式的和叫作多项式.
注意：多项式中含有运算符号，且分母中不含字母.
在多项式里，每个单项式（连同符号）叫作多项式的项.不含字母的项叫作常数项.
注意：多项式的每一项都是单项式，每一项都包括它前面的符号.
练一练：指出下列各式中的多项式，并指出多项式的项.
一个多项式含有几项，这个多项式就叫作几项式.一个多项式里，次数最高的项的次数叫作这个多项式的次数.
下列多项式分别是几次几项式？
整式：单项式与多项式统称为整式.
注意：所有的单项式与多项式都是整式；既不是单项式也不是多项式的式子一定不是整式.
1.判断正误:（1）x是一次单项式. （ ）（2）-1不是单项式. （ ）（3）单项式xy没有系数. （ ）（4）23x2是五次单项式. （ ）（5）3x+y是二次二项式. （ ）
【选自教材P68练习 第1题】
【选自教材P68练习第2题】
【选自教材P68练习第3题】
3.下列多项式是几次几项式？指出它们的最高次项和常数项.（1）-2x+1；（2）3x-4x2-1；（3）x2-xy+y2；（4）-mn-m+2.
一次二项式；最高次项为-2x，常数项为1
二次三项式；最高次项为-4x2，常数项为-1
二次三项式；最高次项为x2，-xy，y2，无常数项
二次三项式；最高次项为-mn，常数项为2
4.已知2x4-my是关于x，y的三次单项式，则m的值为_______.
5.当m=______时，代数式 是关于x的一次单项式.
6.已知(m+1)x3-(n-2)x2+(m+5)x-6是关于x的多项式.（1）当m，n满足什么条件时，该多项式是关于x的二次多项式？（2）当m，n满足什么条件时，该多项式是关于x的三次二项式？
解：（1）由题意得 m+1=0，且-(n-2)≠0.所以 m=-1，n≠2.则当 m=-1，n≠2 时，该多项式是关于x的二次多项式.（2）由题意得m+1≠0，且-(n-2)=0，m+5=0所以 n=2，m=-5.则当m=-5，n=2时，该多项式是关于x的三次二项式.
次数: 所有字母的指数的和.
系数：单项式中的数字因数.
项：式中的每个单项式叫多项式的项.
（其中不含字母的项叫做常数项）
次数：多项式中次数最高的项的次数.