华师大版七年级上册第5章 相交线与平行线5.2 平行线1 平行线一课一练

这是一份华师大版七年级上册第5章 相交线与平行线5.2 平行线1 平行线一课一练，共7页。
【学习目标】
熟练掌握对顶角，邻补角及垂线的概念及性质，了解点到直线的距离与两平行线间的距离的概念；
2. 区别平行线的判定与性质，并能灵活运用；
3. 了解平移的概念及性质.
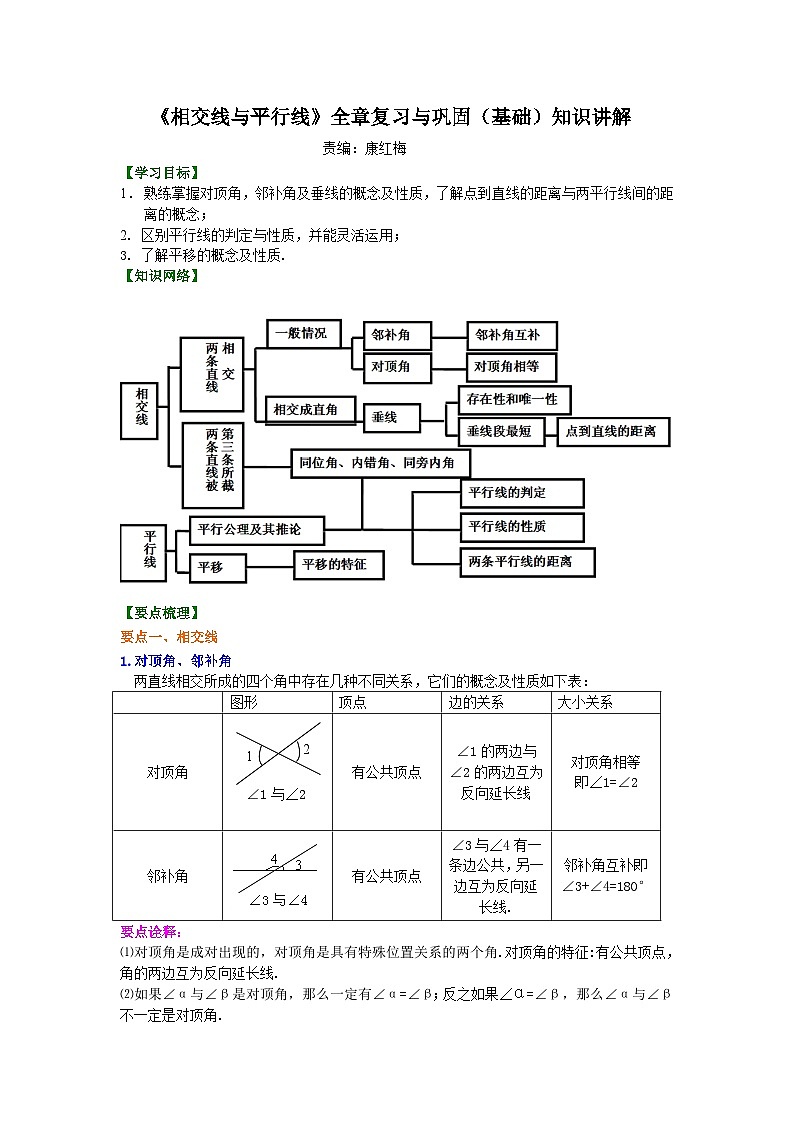
【知识网络】
【要点梳理】
要点一、相交线
1.对顶角、邻补角
两直线相交所成的四个角中存在几种不同关系，它们的概念及性质如下表：
要点诠释：
⑴对顶角是成对出现的，对顶角是具有特殊位置关系的两个角.对顶角的特征:有公共顶点，角的两边互为反向延长线.
⑵如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角.
⑶如果∠α与∠β互为邻补角，则一定有∠α+∠β=180°；反之如果∠α+∠β=180°，则∠α与∠β不一定是邻补角.邻补角的特征:有公共顶点，有一条公共边，另一边互为反向延长线．
⑶两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个.
2.垂线及性质、点到直线的距离
（1）垂线的定义：
当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足.如图1所示，符号语言记作： AB⊥CD，垂足为O.
要点诠释：
要判断两条直线是否垂直，只需看它们相交所成的四个角中，是否有一个角是直角，两条线段垂直，是指这两条线段所在的直线垂直.
（2）垂线的性质：
垂线性质1：过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记).
垂线性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短.简称：垂线段最短.
（3）点到直线的距离：
直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，如图2：PO⊥AB，点P到直线AB的距离是垂线段PO的长.
要点诠释：垂线段PO是点P到直线AB所有线段中最短的一条.
要点二、平行线
1．平行线的判定
判定方法1：同位角相等，两直线平行．
判定方法2：内错角相等，两直线平行．
判定方法3：同旁内角互补，两直线平行．
要点诠释：根据平行线的定义和平行公理的推论，平行线的判定方法还有：
（1）平行线的定义：在同一平面内，如果两条直线没有交点（不相交），那么两直线平行.
（2）如果两条直线都平行于第三条直线，那么这两条直线平行（平行线的传递性）.
（3）在同一平面内，垂直于同一直线的两条直线平行.
（4）平行公理：经过直线外一点，有且只有一条直线与这条直线平行.
2．平行线的性质
性质1：两直线平行，同位角相等；
性质2：两直线平行，内错角相等；
性质3：两直线平行，同旁内角互补.
要点诠释：根据平行线的定义和平行公理的推论，平行线的性质还有：
（1）若两条直线平行，则这两条直线在同一平面内，且没有公共点．
（2）如果一条直线与两条平行线中的一条直线垂直，那么它必与另一条直线垂直．
3．两条平行线间的距离
如图3，直线AB∥CD，EF⊥AB于E，EF⊥CD于F，则称线段EF的长度为两平行线AB与CD间的距离.
要点诠释：
（1）两条平行线之间的距离处处相等.
（2）初中阶级学习了三种距离,分别是两点间的距离、点到直线距离、平行线间的距离.这三种距离的共同点在于都是线段的长度,它们的区别是两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度, 平行线间的距离是一条直线上的一点到与之平行的另一直线的距离.
（3）如何理解 “垂线段”与 “距离”的关系：垂线段是一个图形，距离是线段的长度，是一个量，它们之间不能等同.
要点三、图形的平移
在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移．
要点诠释：平移的性质：
（1）平移后，对应线段平行（或共线）且相等；
（2）平移后，对应角相等；
（3）平移后，对应点所连线段平行（或共线）且相等；
（4）平移后，新图形与原图形是一对全等图形.
【典型例题】
类型一、相交线
1.如图，直线AB、CD、EF相交于点O，那么互为对顶角（平角除外）的角共有 对，它们分别是 ，共有 对邻补角.
【思路点拨】根据邻补角定义和对顶角定义，每一个顶点处有四个角，可以组成四对邻补角和两对对顶角，而本题图形中，三个顶点重叠在一起，所以再乘以3即可．
【答案】6,∠AOC与∠BOD，∠AOF与∠BOE，∠COF与∠DOE, ∠BOC与∠AOD，∠BOF与∠AOE, ∠DOF与∠COE ,12
【解析】找对顶角或邻补角，先从某一个角开始，顺时针或逆时针旋转，这样做，既不漏也不重.
【总结升华】两条直线相交得到的四个角中，共有2对对顶角，4对邻补角.
举一反三：
【变式】（ •贺州）如图，下列各组角中，是对顶角的一组是（ ）
A．∠1和∠2 B．∠3和∠5 C．∠3和∠4 D．∠1和∠5
【答案】B．
2.已知：如图，直线a、b、c两两相交，且a⊥b，∠1＝2∠3，，求∠4的度数.
【答案与解析】
解：∵a⊥b,
∴∠2＝∠1＝90°.
又∵∠1＝2∠3，∴90°＝2∠3，∴∠3＝45°,
又∠3与∠4互为邻补角，
所以∠3+∠4＝180°即45°+∠4＝180°.
所以∠4＝135°.
【总结升华】涉及到角的运算时，充分利用已知条件和隐含条件（平角、余角、补角、对顶角等）是解题的关键．
类型二、平行线的性质与判定
3. （ •诏安县校级模拟）如图，已知：AB∥DE，∠1=∠2，直线AE与DC平行吗？请说明理由．
【答案与解析】
答：AE∥DC；
理由如下：
∵AB∥DE（已知），
∴∠1=∠3（两直线平行，内错角相等），
∵∠1=∠2（已知），
∴∠2=∠3（等量代换），
∴AE∥DC（内错角相等，两直线平行）．
【总结升华】此题主要考查了平行线的判定与性质，关键是掌握两直线平行，内错角相等；内错角相等，两直线平行．
举一反三：
【变式】如图，已知∠ADE＝∠B，∠1＝∠2，那么CD∥FG吗？并说明理由.
【答案】
解：平行，理由如下：
因为∠ADE=∠B，所以DE∥BC（同位角相等，两直线平行），
所以∠1=∠BCD（两直线平行，内错角相等）.
又因为∠1=∠2（已知），
所以∠BCD=∠2.
所以CD∥FG（同位角相等，两直线平行）.
【高清课堂：相交线与平行线单元复习 403105经典例题3】
4.如图，已知∠1＋∠2＝180°，∠3＝∠B，试判断∠AED与∠ACB的大小关系，并说明理由．
【答案与解析】∠AED=∠ACB，理由如下：
∵∠1＋∠2＝180°，又∠1＋∠4＝180°,
∴∠2＝∠4.
∴AB∥EF（内错角相等，两直线平行）.
∴∠5＝∠3.
又∠3=∠B,
∴∠5＝∠B.
∴DE∥BC（同位角相等，两直线平行）.
∴∠AED=∠ACB(两直线平行,同位角相等).
【总结升华】反复应用平行线的判定与性质，见到角相等或互补，就应该想到判断直线是否平行，见到直线平行就应联想到角相等或互补.
类型三、图形的平移
5.如图(1)，线段AB经过平移有一端点到达点C，画出线段AB平移后的线段CD．

【思路点拨】连接AC或BC便得平移的方向和距离．
【答案与解析】
解：如图(2)，线段CD有两种情况：(1)当点A平移到点C时，则点D在点C的下方，因此下边线段CD即为所求；(2)当点B平移到点C时，则点D在点C的上方，上边线段CD即为所求．
【总结升华】平移是由平移的方向和距离决定的．本题中未指明哪一端点(A还是B)移动到点C，故应有两种情况：即点A平移到点C或点B平移到点C．
举一反三：
【变式】下列说法错误的是（ ）
A．平移不改变图形的形状和大小
B．平移中图形上每个点移动的距离可以不同
C．经过平移，图形的对应线段、对应角分别相等
D．经过平移，图形对应点的连线段相等
【答案】B
类型四、实际应用
6.如图，107国道上有一个出口M，想在附近公路旁建一个加油站，欲使通道最短，应沿怎样的线路施工？
【答案与解析】
解：如图，过点M作MN⊥，垂足为N，欲使通道最短，应沿线路MN施工.
【总结升华】灵活运用垂线段最短的性质是解答此类问题的关键.图形
顶点
边的关系
大小关系
对顶角
1
2
∠1与∠2
有公共顶点
∠1的两边与
∠2的两边互为反向延长线
对顶角相等
即∠1=∠2
邻补角
有公共顶点
∠3与∠4有一条边公共，另一边互为反向延长线.
邻补角互补即
∠3+∠4=180°