华师大版七年级上册1 点和线导学案

这是一份华师大版七年级上册1 点和线导学案，共8页。学案主要包含了学习目标，要点梳理，典型例题，思路点拨，答案与解析，总结升华等内容，欢迎下载使用。
【学习目标】
1. 理解点和线是最基本的图形；
2．在现实情境中进一步理解线段、射线、直线，并会用不同的方式表示；
3. 通过操作活动，了解“两点确定一条直线”的几何事实，积累数学活动经验；
4. 能够运用几何事实解释和解决具体情境中的实际问题；
5. 通过从事观察、比较、概括等活动，发展抽象思维能力和有条理的数学表达能力.
【要点梳理】
要点一、点、线、面、体
长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体；包围着体的是面,面有平的面和曲的面两种；面和面相交的地方形成线，线也分为直线和曲线两种；线和线相交的地方形成点.
要点二、线段、射线、直线的概念及表示方法
1.概念：一根拉紧的绳子、一根竹竿、人行横道线都给我们以线段的形象，如果把“线段”作为最简单、最基本原始概念，则用“线段”定义射线和直线如下：
（1）把线段向一方无限延伸所形成的图形叫做射线.
（2）把线段向两方无限延伸所形成的图形叫做直线．
要点诠释：
（1）线段有两个端点，可以度量，可以比较长短．
（2）射线只向一方无限延伸，有一个端点，不能度量，不能比较大小.
（3）直线是向两方无限延伸的，无端点，不可度量，不能比较大小.
（4）线段、射线、直线都没有粗细．
2.表示方法：如图1、图2、图3，线段、射线、直线的表示方法都有两种：它们都可以用两个大写字母表示，也可以一个小写字母表示.
要点诠释：
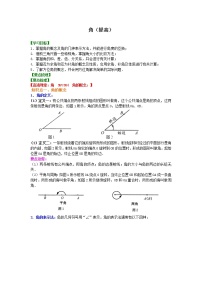
（1）从表示方法上看，虽然它们都可以用一个小写字母表示，也可以用两个大写字母表示，但直线取得是直线上任意两点的字母，线段用的是两个端点的字母，射线用的是一个端点和任意一点的字母，而直线和线段的两个大写字母没有顺序之分，但射线的两个大写字母有顺序之分，第一个大写字母必须是表示端点.即端点相同，而延伸方向不同，表示不同的射线．如下图4中射线OA，射线OB是不同的射线；
图4

端点相同且延伸方向也相同的射线，表示同一条射线．如下图5中射线OA、射线OB、射线OC都表示同一条射线．
图5
（2）表示直线、射线与线段时，勿忘在字母的前面写上“直线”“射线”“线段”字样．
3.线段、射线、直线的区别与联系
要点三、直线、线段的基本性质
1. 直线的性质：经过两点有一条直线，并且只有一条直线.即两点确定一条直线．
要点诠释：
（1）点和直线的位置关系有两种：
①点在直线上，或者说直线经过这个点.如图6中，点O在直线l上，也可以说成是直线l经过点O；
②点在直线外，或者说直线不经过这个点.如图6中，点P在直线l外，也可以说直线l不经过点P.
（2）两条不同的直线相交只有一个交点.
2.线段的基本性质：两点的所有连线中，线段最短．简记为：两点之间，线段最短．
如图7所示，在A，B两点所连的线中，线段AB的长度是最短的．
图7
要点诠释：
（1）连接两点间的线段的长度，叫做这两点的距离．
（2）两条线段可能无公共点，可能有一个公共点，也可能有无穷多个公共点.
要点四、线段的长短比较
1. “作一条线段等于已知线段”的两种方法：
法一：用圆规作一条线段等于已知线段．例如：下图所示，用圆规在射线AC上截取AB＝a．
法二：用刻度尺作一条线段等于已知线段．例如：可以先量出线段a的长度，再画一条等于这个长度的线段．
要点诠释：几何中连结两点，即画出以这两点为端点的线段.
2.线段的比较：
（1）度量法：用刻度尺量出两条线段的长度，再比较长短．
（2）叠合法：利用直尺和圆规把线段放在同一条直线上，使其中一个端点重合，另一个端点位于重合端点同侧，根据另一端点与重合端点的远近来比较长短．如下图：
要点诠释：类似于数，线段也可以相加减．
3.线段的中点：把一条线段分成两条相等线段的点，叫做线段的中点．如下图，点C是线段AB的中点，则，或AB＝2AC＝2BC．
要点诠释：若点C是线段AB的中点，则点C一定在线段AB上．
【典型例题】
类型一、点、线、面、体
1．8世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：
(1)根据上面多面体模型，完成表格中的空格：

你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______ _；
(2)一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是________；
(3)某个玻璃饰品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱．设该多面体外表面三角形的个数为x个，八边形的个数为y个，求x+y的值．
【思路点拨】根据四面体、长方体、正八面体，正十二面体的顶点数、面数和棱数，总结出顶点数（v）、面数（F）、棱数（E）之间存在的关系式，再用这个关系式解答后面的问题.
【答案与解析】
解：(1)6， 6， V+F-E＝2；
(2)20；
(3)这个多面体的面数为x+y，棱数为条，
根据V+F-E＝2可得24+(x+y)-36＝2，
∴ x+y＝14．
【总结升华】欧拉公式：V（顶点数）+F（面数）-E（棱数）＝2
举一反三：
【变式】如图把一个圆绕虚线旋转一周，得到的几何体是（ ）
A. B. C. D.
【答案】B
类型二、线段、射线、直线的概念及表示方法
2.如图所示，指出图中的直线、射线和线段．
【思路点拨】从图上看，A、D、F分别是线段CB、BC、BE的延长线上的点，也就是说，A、D、F三点的位置并不是完全确定的．此时，我们也就能分清楚图中的直线、射线和线段了．
【答案与解析】
解：直线有一条：直线AD；
射线有六条：射线BA、射线BD、射线CA、射线CD、射线BF、射线EF；
线段有三条：线段BC、线段BE、线段CE．
【总结升华】在表示线段和直线时，两个大写字母的顺序可以颠倒．然而，在叙述线段的延长线的时候，表示线段的两个大写字母的顺序就不能颠倒了，因为线段向一方延伸后就形成了射线(延长部分已不再是线段本身了)，而表示射线的两个大写字母的顺序是不能颠倒的，只能用第一个字母表示射线的端点，第二个字母表示射线方向上的任一点．
举一反三：
【高清课堂：直线、射线、线段397363 拓展4】
【变式】两条不同的直线，要么有一个公共点，要么没有公共点，不能有两个公共点. 这是为什么?画图说明.
【答案】
解：


∵过两点有且只有一条直线.（或两点确定一条直线.）
∴两条不同的直线，要么有一个公共点，如图（1）；要么没有公共点，如图（2）；不能有两个公共点.
类型三、线段、射线、直线有关作图
3．（ 春•高青县期中）已知平面上四点A、B、C、D，如图：
（1）画直线AD；
（2）画射线BC，与AD相交于O；
（3）连结AC、BD相交于点F．
【思路点拨】（1）画直线AD，连接AD并向两方无限延长；（2）画射线BC，以B为端点向BC方向延长交AD于点O；（3）连接各点，其交点即为点F．
【答案与解析】
解：如图所示：
【总结升华】本题主要考查直线、射线、线段的认识，掌握直线、射线、线段的特点是解题的关键．
举一反三：
【变式1】下列说法正确的有 ( )
①射线与其反向延长线成一条直线；
②直线a、b相交于点m；
③两直线相交于两个交点；
④直线A与直线B相交于点M
A．3个 B．2个 C．1个 D．4个
【答案】 C
【变式2】下列说法中，正确的个数有( )
①已知线段a，b且a-b＝c，则c的值不是正的就是负的；
②已知平面内的任意三点A，B，C则AB+BC≥AC；
③延长AB到C，使BC＝AB，则AC＝2AB；
④直线上的顺次三点D、E、F，则DE+EF＝DF．
A．1个 B．2个 C．3个 D．4个
【答案】C
类型四、有关条（个）数及长度的计算
4. 根据题意，完成下列填空．
如图所示，与是同一平面内的两条相交直线，它们有1个交点，如果在这个平面内，再画第3条直线，那么这3条直线最多有________个交点；如果在这个平面内再画第4条直线，那么这4条直线最多可有________个交点．由此我们可以猜想：在同一平面内，6条直线最多可有________个交点，n(n为大于1的整数)条直线最多可有________个交点(用含有n的代数式表示)．
【答案】3， 6， 15， .
【解析】本题探索过程要分两步：首先要填好3条直线最多可有2+1＝3个交点，再类推4条直线，5条直线，6条直线的情形所得到的和式，其次再研究这些和式的规律，得出一般性的结论．
【总结升华】n(n为大于1的整数)条直线的交点最多可有：个.
举一反三：
【变式1】平面上有个点，最多可以确定 条直线.
【答案】
【变式2】一条直线有个点，最多可以确定 条线段， 条射线.
【答案】，
【高清课堂：直线、射线、线段397363 拓展 1（4）】
【变式3】一个平面内有三条直线，会出现几个交点?
【答案】0个，1个，2个，或3个.
5.已知线段AB＝14cm，在直线AB上有一点C，且BC＝4cm，M是线段AC的中点，求线段AM的长．
【思路点拨】题目中只说明了A、B、C三点在同一直线上，无法判定点C在线段AB上，还是在线段AB外(也就是在线段AB的延长线上)．所以要分两种情况求线段AM的长．
【答案与解析】
解：①当点C在线段AB上时，如图所示．
因为M是线段AC的中点，
所以．
又因为AC＝AB-BC，AB＝14cm，BC＝4cm，
所以．
②当点C在线段AB的延长线上时，如图所示．
因为M是线段AC的中点，
所以．
又因为AC＝AB+BC，AB＝14cm，BC＝4cm，
所以9(cm)．
所以线段AM的长为5cm或9cm．
【总结升华】在解答没有给出图形的问题时，一定要审题，要全面考虑所有可能的情况，即当我们面临的教学问题无法确定是哪种情形时，就要分类讨论．
举一反三：
【变式】（ 秋•温州期末）已知点B在直线AC上，线段AB=8cm，AC=18cm，P、Q分别是线段AB、AC的中点，则线段PQ= ．
【答案】13cm或5cm．
解：当点C在点A左侧时，AP=AC=9，AQ=AB=4，
∴PQ=AQ+AP=9+4=13cm．
当点C在点B右侧时，AP=AB=4cm，BC=AC﹣AB=10cm，AQ=，AC=9，PQ=AQ﹣AP=9﹣4=5cm．
故答案为：13cm或5cm．
．
类型五、路程最短问题
6.（ 春•嵊州市期末）某公司员工分别在A、B、C三个住宅区，A区有30人，B区有30人，C区有10人，三个区在同一条直线上，如图所示，该公司的接送车打算在此间只设一个停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠点的位置应设在（ ）
A．A区B．B区C．C区D．A、B两区之间
【答案】B．
【解析】
解：①设在A区、B区之间时，设距离A区x米，
则所有员工步行路程之和=30x+30（100﹣x）+10（100+200﹣x），
=30x+3000﹣30x+3000﹣10x，
=﹣10x+6000，
∴当x最大为100时，即在B区时，路程之和最小，为5000米；
②设在B区、C区之间时，设距离B区x米，
则所有员工步行路程之和=30（100+x）+30x+10（200﹣x），
=3000+30x+30x+2000﹣10x，
=50x+5000，
∴当x最大为0时，即在B区时，路程之和最小，为5000米；
综上所述，停靠点的位置应设在B区．
【总结升华】本题是线段的概念在现实中的应用，根据题意分别计算停靠点分别在各点时员工步行的路程和，选择最小的即可得解.
举一反三：
【变式】如图，从A到B最短的路线是（ ）.
A．A-G-E-B B．A-C-E-B
C．A-D-G-E-B D．A-F-E-B
【答案】D.
线段
射线
直线
图示
表示方法
线段AB或线段a
射线OA或射线a
直线AB或直线a
端点
两个
一个
无
长度
可度量
不可度量
不可度量
延伸性
不向两方延伸
向一方无限延伸
向两方无限延伸