人教B版 (2019)必修 第一册1.2.2 全称量词命题与存在量词命题的否定示范课ppt课件

这是一份人教B版 (2019)必修 第一册1.2.2 全称量词命题与存在量词命题的否定示范课ppt课件，共34页。PPT课件主要包含了∀x∈M¬px，∃x∈M¬qx，－∞1，－∞5，－∞3，a∈Ra≠3等内容，欢迎下载使用。
必备知识·情境导学探新知
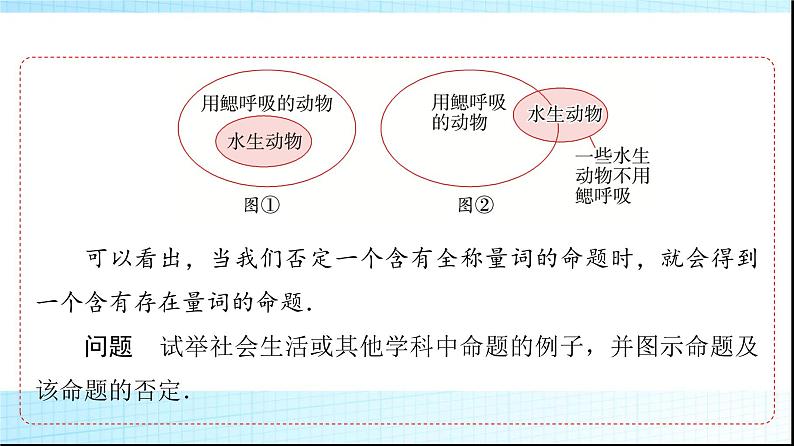
假设我们要否定命题“所有水生动物都用鳃呼吸”，可以这样做：画出表示用鳃呼吸的动物的集合，并包含表示所有水生动物的集合，如图①所示，那么此图就表示“所有水生动物都用鳃呼吸”．再将图①中水生动物的集合部分地移出用鳃呼吸的动物的集合，如图②，那么此图就表示“并非所有水生动物用鳃呼吸”，即“一些水生动物不用鳃呼吸”．这就得到了原命题的否定．
可以看出，当我们否定一个含有全称量词的命题时，就会得到一个含有存在量词的命题．问题　试举社会生活或其他学科中命题的例子，并图示命题及该命题的否定．
知识点1　命题的否定1．定义：一般地，对命题p加以____，就得到一个新的命题，记作“____”，读作“非p”或“p的否定”．2．命题p与其否定¬p的真假关系如果一个命题是真命题，那么这个命题的否定就是一个__命题；反之亦然．
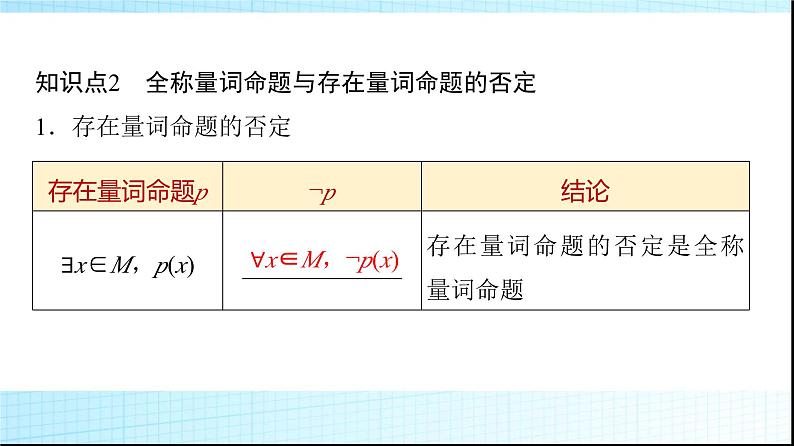
知识点2　全称量词命题与存在量词命题的否定1．存在量词命题的否定
2．全称量词命题的否定
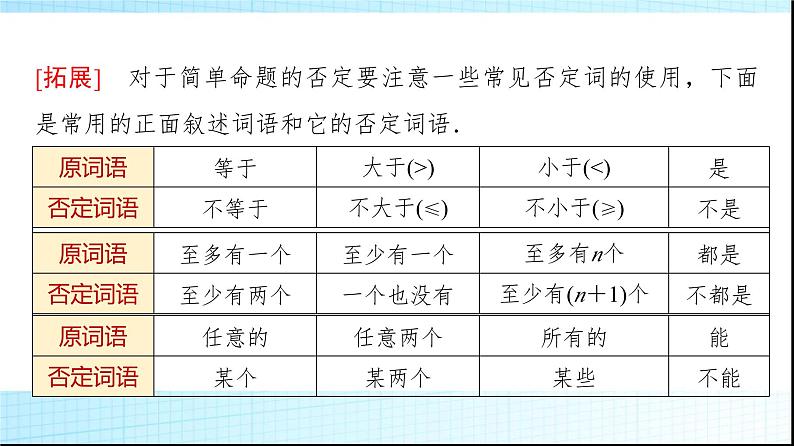
[拓展]　对于简单命题的否定要注意一些常见否定词的使用，下面是常用的正面叙述词语和它的否定词语．
提醒　(1)“x＝0或x＝1”的否定是“x≠0且x≠1”，而不是“x≠0或x≠1”．(2)“x，y全为0”的否定是“x，y不全为0”，而不是“x，y全不为0”．
1．思考辨析(正确的打“√”，错误的打“×”)(1)命题¬p的否定是p．(　　)
[提示]　命题p与¬p互为否定．
[提示]　存在量词命题p与其否定¬p一真一假．
(2)∃x∈M，p(x)与∀x∈M，¬p(x)的真假性相反．(　　)
(3)存在量词命题的否定，是对“量词”和“p(x)”同时否定．(　　)
[提示]　尽管存在量词命题的否定是全称量词命题，只是对“p(x)”进行否定，而将“存在量词”调整为“全称量词”，不能将其理解为“同时否定”．
2．若命题p：函数y＝1－x2的图象过点(－3，2)，则p与¬p的真假情况是(　　)A．都是真命题　　　B．都是假命题C．p真，¬p假D．p假，¬p真
D　[∵p与¬p必一真一假，而本题中p显然是假命题，∴¬p必为真命题．]
3．已知命题p：∀x>2，x3－8>0，那么p的否定是_______________．
∃x>2，x3－8≤0　[命题p为全称量词命题，其否定为存在量词命题，则¬p：∃x>2，x3－8≤0．]
∃x>2，x3－8≤0
关键能力·合作探究释疑难
类型1　全称量词命题的否定【例1】　(源自人教A版教材)写出下列全称量词命题的否定．(1)所有能被3整除的整数都是奇数；(2)每一个四边形的四个顶点在同一个圆上；(3)对任意x∈Z，x2的个位数字不等于3．
[解]　(1)该命题的否定：存在一个能被3整除的整数不是奇数．(2)该命题的否定：存在一个四边形，它的四个顶点不在同一个圆上．(3)该命题的否定：∃x∈Z，x2的个位数字等于3．
反思领悟　1．对全称量词命题否定的两个步骤(1)改变量词：把全称量词换为恰当的存在量词．(2)否定结论：原命题结论中的“是”“成立”等改为“不是”“不成立”等．2．全称量词命题否定后的真假判断方法全称量词命题的否定是存在量词命题，其真假性与全称量词命题相反；要说明一个全称量词命题是假命题，只需举一个反例即可．
[跟进训练]1．写出下列命题的否定，并判断其真假．(1)p：任意n∈Z，则n∈Q；(2)p：等圆的面积相等，周长相等；(3)p：偶数的平方是正数．
[解]　(1)¬p：存在n∈Z，使n∉Q，这是假命题．(2)¬p：存在等圆，其面积不相等或周长不相等，这是假命题．(3)¬p：存在偶数的平方不是正数，这是真命题．
反思领悟　1．对存在量词命题否定的两个步骤(1)改变量词：把存在量词换为恰当的全称量词．(2)否定结论：原命题结论中的“有”“存在”等更改为“没有”“不存在”等．2．存在量词命题否定后的真假判断存在量词命题的否定是全称量词命题，其真假性与存在量词命题相反；要说明一个存在量词命题是真命题，只需要找到一个实例即可．
[跟进训练]2．判断下列命题的真假，并写出这些命题的否定．(1)某些梯形的对角线互相平分；(2)∃x∈R，x3－1＝0；(3)在同圆中，同弧所对的圆周角相等；(4)有些素数是奇数．
[解]　(1)假命题，该命题的否定：任意一个梯形的对角线都不互相平分．(2)真命题，该命题的否定：∀x∈R，x3－1≠0．(3)真命题，该命题的否定：在同圆中，同弧所对的圆周角不相等．(4)真命题，该命题的否定：所有的素数都不是奇数．
类型3　全称量词命题与存在量词命题中的求参问题【例3】　已知命题p：“∃x∈R，x2－2x＋m≤0”是假命题，求实数m的取值范围．
[思路导引]　命题p的否定¬p一定为真命题，可以通过分离参数法，转化为不等式恒成立问题，通过求最值得出m的取值范围；也可以利用二次函数的图象和性质转化为Δ与0的关系，解不等式求解．
[解]　(法一)¬p：∀x∈R，x2－2x＋m>0，是真命题，即m>－x2＋2x＝－(x－1)2＋1，x∈R恒成立，设函数y＝－(x－1)2＋1，由二次函数的性质知，当x＝1时，y最大值＝1，所以m>y最大值＝1，即实数m的取值范围是(1，＋∞)．(法二)¬p：∀x∈R，x2－2x＋m>0，是真命题，设函数y＝x2－2x＋m，由二次函数的图象和性质知，只需方程x2－2x＋m＝0的根的判别式Δ0B．∃x∈R，x2＋1≤0C．∃x∈R，x2＋10，是一个全称量词命题，所以¬p：∃x∈R，x2＋1≤0．故选B．]
2．下列命题的否定为假命题的是(　　)A．∃x∈R，x2＋2x＋2≤0B．∀x∈R，x30，所以∃x∈R，x2＋2x＋2≤0是假命题，故其否定为真命题；对于选项B，因为当x≥1时，x3≥1，所以∀x∈R，x3a”的否定是假命题，即“∀x∈(3，＋∞)，x>a”是真命题，故x>a，∀x∈(3，＋∞)恒成立．又x>3，所以a≤3，则实数a的取值范围是(－∞，3]．]
3．若“∀x∈(3，＋∞)，x>a”的否定是假命题，则实数a的取值范围是____________．
{a∈R|a≠3}　[因为“∃x∈R，(a－3)x＋1＝0”是真命题，所以关于x的方程(a－3)x＋1＝0有实数解，所以a－3≠0，即a≠3，所以实数a的取值范围是{a∈R|a≠3}．]
4．已知命题p：“∃x∈R，(a－3)x＋1＝0”是真命题，则实数a的取值范围是_________________．
[提示]　(1)确定命题类型：命题是全称量词命题还是存在量词命题．(2)改变量词：把全称量词改为恰当的存在量词；把存在量词改为恰当的全称量词．(3)否定结论：原命题中的“是”“有”“存在”“成立”等改为“不是”“没有”“不存在”“不成立”等．(4)无量词的全称量词命题要先补回量词再否定．
回顾本节知识，自主完成以下问题：1．对含有一个量词的命题的否定要注意哪些问题？