吉林省部分名校2023-2024学年高二上学期10月联考数学试卷(含答案)

这是一份吉林省部分名校2023-2024学年高二上学期10月联考数学试卷(含答案)，共16页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．直线l经过两点,,则l的斜率为( )
A.B.C.D.
2．直线在x轴上的截距为a,在y轴上的截距为b,则( )
A.,B.,C.,D.,
3．若,,三点共线,则( )
A.4B.-2C.1D.0
4．若直线l的斜率,则直线l的倾斜角的取值范围是( )
A.B.
C. D.
5．若某等腰直角三角形斜边所在直线的倾斜角为,则该三角形两条直角边所在直线的斜率之和为( )
A.0B.C.D.
6．直线l过点,且方向向量为,则( )
A.直线l的点斜式方程为B.直线l的斜截式方程为
C.直线l的截距式方程为D.直线l的一般式方程为
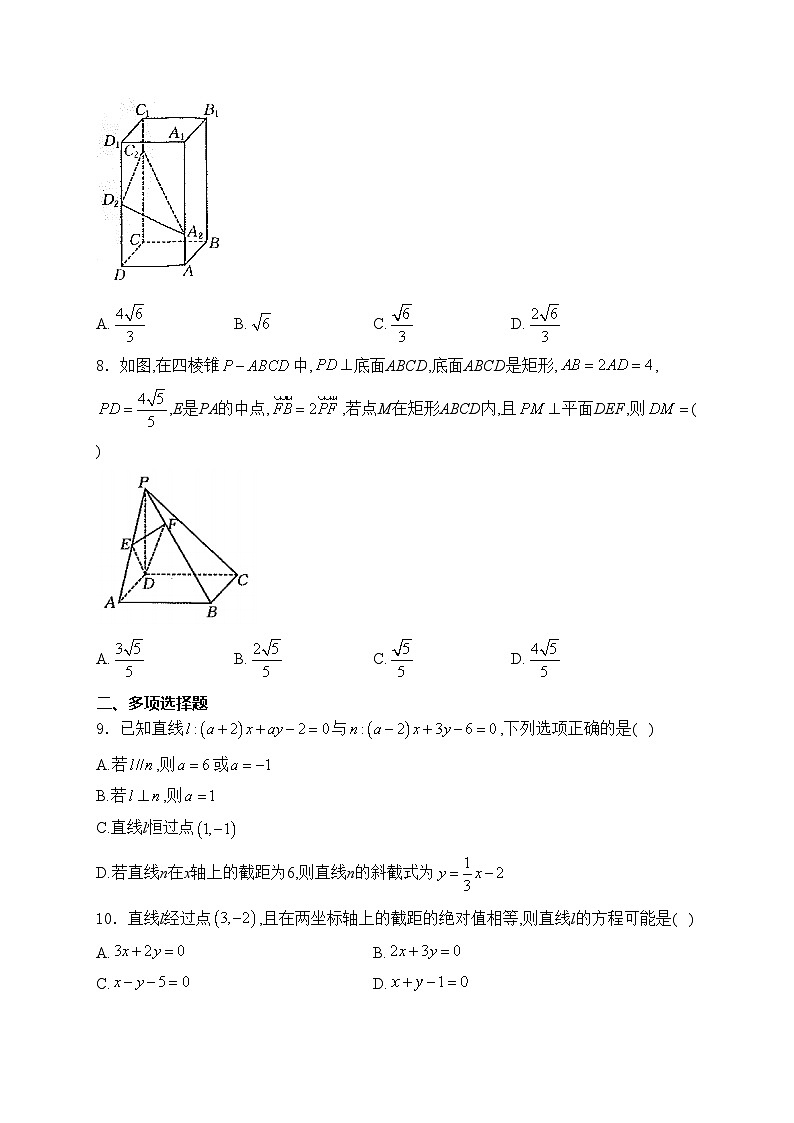
7．如图,在正四棱柱中,,.点,,分别在棱,,上,,,,则点D到平面的距离为( )
A.B.C.D.
8．如图,在四棱锥中,底面ABCD,底面ABCD是矩形,,,E是PA的中点,,若点M在矩形ABCD内,且平面DEF,则( )
A.B.C.D.
二、多项选择题
9．已知直线与,下列选项正确的是( )
A.若,则或
B.若,则
C.直线l恒过点
D.若直线n在x轴上的截距为6,则直线n的斜截式为
10．直线l经过点,且在两坐标轴上的截距的绝对值相等,则直线l的方程可能是( )
A.B.
C.D.
11．已知点,直线,则下列说法中正确的有( )
A.直线l恒过点
B.若直线l与线段PQ有交点,则
C.点P到直线l的距离的最大值为
D.若为直线l上一点,则的最小值为
12．清初著名数学家孔林宗曾提出一种“蒺藜形多面体”,其可由两个正交的正四面体组合而成,如图1,也可由正方体切割而成,如图2,在图2所示的“蒺藜形多面体”中,若,则给出的说法中正确的是( )
A.该几何体的表面积为
B.该几何体的体积为4
C.二面角的余弦值为
D.若点P,Q在线段BM,CH上移动,则PQ的最小值为
三、填空题
13．平行线与间的距离为_____________.
14．若向量,,且,则____________.
15．如图,在圆锥SO中,AB是底面圆O的直径,D,E分别为SO,SB的中点,,,则直线AD与直线CE所成角的余弦值为_____________.
16．在正四棱台中,,,,,,若平面,则_____________.
四、解答题
17．已知直线的斜率为2,直线过点,.
（1）若直线的倾斜角为,求m的值;
（2）若,求m的值.
18．已知的三个顶点的坐标分别为,,.
（1）求点A到直线BC的距离;
（2）求BC边上的高所在直线的方程.
19．如图,在直四棱柱中,,,,E,F,G分别为棱,,的中点.
（1）求的值;
（2）证明：C,E,F,G四点共面.
20．如图,在正方体中,E,F,G分别是,BC,AD的中点.
（1）证明：.
（2）求直线与平面所成角的正弦值.
21．已知的顶点,边AB上的中线所在直线方程为,边AC上的高所在直线方程为.
（1）求顶点B,C的坐标;
（2）求的面积.
22．如图,在四面体ABCD中,,,,,,E,F,G分别为棱BC,AD,CD的中点,点H在线段AB上.
（1）若平面AEG,试确定点H的位置,并说明理由;
（2）求平面AEG与平面CDH的夹角的取值范围.
参考答案
1．答案：A
解析：由,得l的斜率为.
2．答案：B
解析：令,解得,故;令,解得,故.
3．答案：A
解析：因为,,
所以,解得.故.
4．答案：B
解析：设直线l的倾斜角为,其中,可得,
因为,即,
结合正切函数的图象与性质,可得直线的倾斜角．
故选：B.
5．答案：B
解析：不妨作草图,如图所示,因为直线OA的倾斜角为,,
所以直线OB的倾斜角为,直线AB的倾斜角为.
6．答案：D
解析：因为直线l的方向向量为,所以直线l的斜率为2．
因为直线l过点,
所以直线l的点斜式方程为,
其一般式为．故A错误,D正确；
化为斜截式：,故B错误；
化为截距式：,故C错误.
故选：D.
7．答案：D
解析：以C为坐标原点,CD,CB,所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则,,,,,,.
设平面的法向量为,
则令,得.
点D到平面的距离为.
8．答案：D
解析：如图,以D为坐标原点,,,的方向分别为x,y,z轴的正方向,
建立空间直角坐标系,
则,,,,,.
设平面DEF的法向量为,
则,令,得.
设,则.
因为平面DEF,所以,则,解得,.
故.
9．答案：AC
解析：若,则,解得或,
经检验,均符合,故A正确;
若,则,解得或,故B不正确;
由得所以l恒过点,故C正确;
若直线n在x轴上的截距为6,则,得,所以直线n的方程为,
斜截式为,故D不正确.
10．答案：BCD
解析：当直线l的截距为0时,此时直线l的方程为,即．
当直线l的截距不为0时,设直线l的方程为,
则,解得或,
当,时,可得直线l的方程为,即；
若,时,可得则直线l的方程为,即．
故选：BCD.
11．答案：BCD
解析：对于A,因为直线l的方程可化为,令且,所以直线l过定点,故A错误．
对于B,如下图,因为直线l过定点,且,所以,故B正确．
对于C,当直线时,点P到直线l的距离最大,且最大值为,故C正确．
对于D,如下图,当时,直线l的方程为．
设P关于直线l的对称点为,则解得,
所以,所以,故D正确．
故选：BCD.
12．答案：BCD
解析：因为,所以.该几何体的表面积为,A错误.
该几何体的体积为,B正确.
设EF的中点为O,连接OB,OH（图略）,则即二面角的平面角.
,,C正确.
建立如图所示的空间直角坐标系,
设,,
,
当且仅当,时,等号成立.故PQ的最小值为,D正确.
13．答案：
解析：将方程两边乘以2,得,
所以该两平行线间的距离为.
14．答案：3
解析：,.因为,所以,解得.
15．答案：
解析：以点O为坐标原点,建立如图所示的空间直角坐标系,
则,,,,,
,.
16．答案：
解析：连接,设,平面平面.
因为平面,所以.,,
,,
因为,所以.
17．答案：（1）2
（2）
解析：（1）因为直线的倾斜角为,所以直线的斜率为,
所以,解得.
（2）因为,直线的斜率为2,所以直线的斜率为,
所以,解得.
18．答案：（1）
（2）
解析：（1）,
直线BC的方程为,即.
点A到直线BC的距离为.
（2）结合（1）可得,BC边上的高所在直线的斜率为.
BC边上的高所在直线的方程为,即.
19．答案：（1）6
（2）见解析
解析：（1）以点A为坐标原点,AD,,AB所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则,,,.
,.
.
（2）证明：.
令,即
解得所以.故C,E,F,G四点共面.
20．答案：（1）见解析
（2）见解析
解析：（1）设正方体的棱长为2,以D为原点,建立如图所示的空间直角坐标系,
则,,,,,,.
,,,.
证明：因为,所以,即.
（2）因为,所以,即.
因为,所以平面,即为平面的一个法向量.
设直线与平面所成的角为,则.
故直线与平面所成角的正弦值为.
连接（图略）.
在正方体中,平面,所以.
因为,所以.
在正方形中,E,G分别是边,AD的中点,可得,
所以,,所以.
因为,所以平面.
因为平面,所以.
21．答案：（1）
（2）
解析：（1）设,因为边AB上的中线所在直线方程为,
边AC上的高所在直线方程为,
所以,解得,即B的坐标为.
设,因为边AB上的中线所在直线方程为,
边AC上的高所在直线方程为,
所以,解得,即C的坐标为.
（2）因为,,所以.
因为边AB所在直线的方程为,即,
所以点到边AB的距离为,即边AB上的高为,
故的面积为.
22．答案：（1）见解析
（2）
解析：（1）若平面AEG,则H为AB的中点,理由如下：
因为E,G分别为BC,CD的中点,所以.
因为平面AEG,所以平面AEG.
若平面AEG,只需即可.
因为F为AD的中点,所以H为AB的中点.
（2）过点D作平面ABC,垂足为O,连接OE,OA.
设,因为,,
所以,,,
.
在中,,.
因为,所以,解得.
所以.
以C为坐标原点,建立如图所示的空间直角坐标系,
则,,,.
过点H作,垂足为M,作,垂足为N.
设,则,,
所以.
,,,
设平面AEG的法向量为,
则,令,则.
设平面CDH的法向量为,
则令,则.
.
当时,.
当时,.
令,则.
函数在上单调递增,
所以,,即.
故,平面AEG与平面CDH的夹角的取值范围为.