

艺术生高考数学专题讲义:考点43 双曲线
展开1.双曲线的概念
把平面内到两定点F1,F2的距离之差的绝对值等于常数(大于零且小于|F1F2|)的点的集合叫作双曲线.定点F1,F2叫作双曲线的焦点,两个焦点之间的距离叫作双曲线的焦距.
用集合语言表示为:P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.
说明:定义中,到两定点的距离之差的绝对值小于两定点间距离非常重要.令平面内一点到两定点F1,F2的距离的差的绝对值为2a(a为常数),则只有当2a<|F1F2|且2a≠0时,点的轨迹才是双曲线;若2a=|F1F2|,则点的轨迹是以F1,F2为端点的两条射线;若2a>|F1F2|,则点的轨迹不存在.
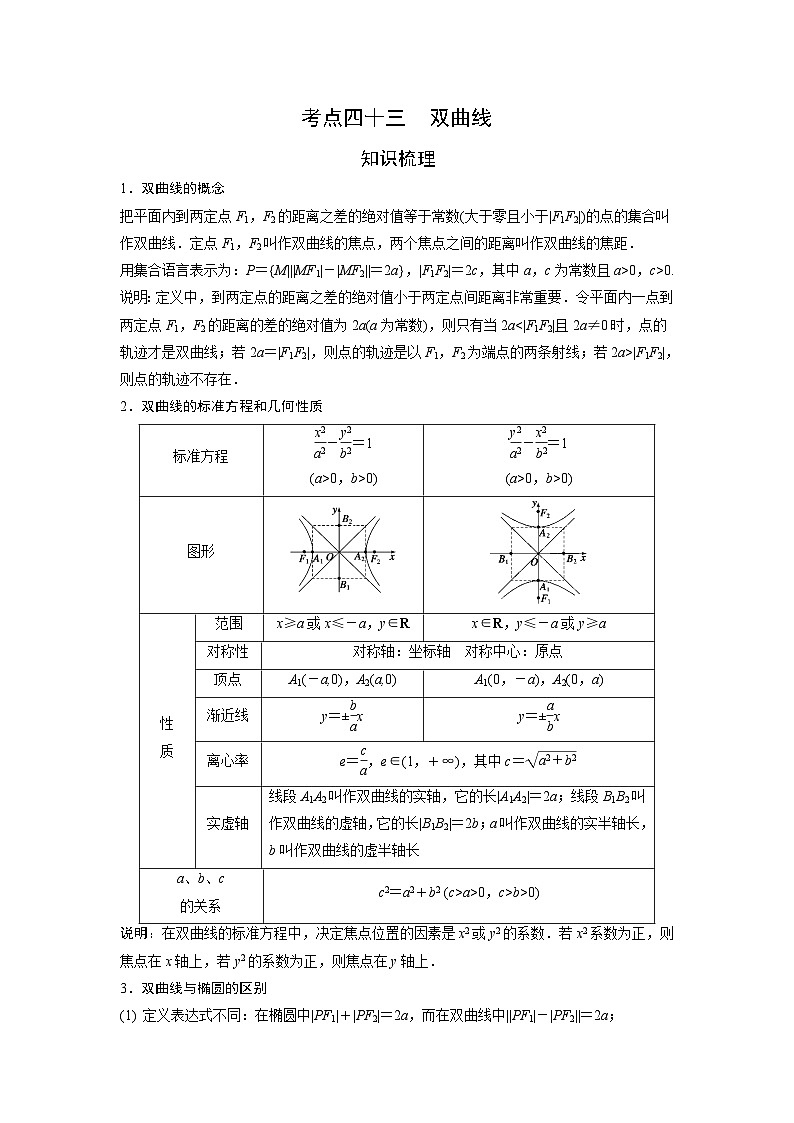
2.双曲线的标准方程和几何性质
说明:在双曲线的标准方程中,决定焦点位置的因素是x2或y2的系数.若x2系数为正,则焦点在x轴上,若y2的系数为正,则焦点在y轴上.
3.双曲线与椭圆的区别
(1) 定义表达式不同:在椭圆中|PF1|+|PF2|=2a,而在双曲线中||PF1|-|PF2||=2a;
(2) 离心率范围不同:椭圆的离心率e∈(0,1),而双曲线的离心率e∈(1,+∞);
(3) a,b,c的关系不同:在椭圆中a2=b2+c2,a>c;而在双曲线中c2=a2+b2, c>a.
典例剖析
题型一 双曲线的定义和标准方程
例1 设双曲线C的两个焦点为(-eq \r(2),0),(eq \r(2),0),一个顶点是(1,0),则C的方程为________.
答案 x2-y2=1
解析 由题意可知,双曲线的焦点在x轴上,且c=eq \r(2),a=1,则b2=c2-a2=1,
所以双曲线C的方程为x2-y2=1.
变式训练 与椭圆C:eq \f(y2,16)+eq \f(x2,12)=1共焦点且过点(1,eq \r(3))的双曲线的标准方程为________.
答案 eq \f(y2,2)-eq \f(x2,2)=1
解析 椭圆eq \f(y2,16)+eq \f(x2,12)=1的焦点坐标为(0,-2),(0,2),
设双曲线的标准方程为eq \f(y2,m)-eq \f(x2,n)=1(m>0,n>0),则eq \b\lc\{(\a\vs4\al\c1(\f(3,m)-\f(1,n)=1,m+n=4)),解得m=n=2.
∴双曲线的标准方程为eq \f(y2,2)-eq \f(x2,2)=1.
解题要点 求双曲线的标准方程的基本方法是定义法和待定系数法.在求解时,注意巧设方程,可以减少讨论以及计算的难度,一般来说:
(1)与双曲线eq \f(x2,a2)-eq \f(y2,b2)=1 (a>0,b>0)有共同渐近线的方程可表示为eq \f(x2,a2)-eq \f(y2,b2)=t (t≠0).
(2)过已知两个点的双曲线方程可设为eq \f(x2,m)-eq \f(y2,n)=1 (mn>0),也可设为Ax2+By2=1 (AB<0),这种形式在解题时更简便.
题型二 双曲线的离心率
例2 已知双曲线eq \f(x2,a2)-eq \f(y2,3)=1(a>0)的离心率为2,则a=________.
答案 1
解析 由题,c=2a. ∴c2=4a2,又c2=a2+3,∴4a2=a2+3,a2=1,
∵a>0,∴ a=1.
变式训练 若双曲线eq \f(x2,a2)-eq \f(y2,b2)=1 (a>0,b>0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为________.
答案 eq \r(5)
解析 由题意得b=2a,又a2+b2=c2,∴5a2=c2.
∴e2=eq \f(c2,a2)=5,∴e=eq \r(5).
解题要点 1.注意双曲线中a,b,c的关系,在双曲线中c2=a2+b2, c>a.
2. 注意离心率公式及其变式运用,e=eq \f(c,a)eq \r(\f(c2,a2))=eq \r(\f(a2+b2,a2))=eq \r(1+\f(b2,a2)),
e=eq \r(\f(c2,c2-b2))= eq \r(\f(1,1-\f(b2,c2))) .
题型三 双曲线的渐近线
例3 设双曲线C经过点(2,2),且与eq \f(y2,4)-x2=1具有相同渐近线,则C的方程为________;渐近线方程为________.
答案 eq \f(x2,3)-eq \f(y2,12)=1 y=±2x
解析 设双曲线C的方程为eq \f(y2,4)-x2=λ,将点(2,2)代入上式,得λ=-3,
∴C的方程为eq \f(x2,3)-eq \f(y2,12)=1,其渐近线方程为y=±2x.
变式训练 已知双曲线C:eq \f(x2,n)-eq \f(y2,4-n)=1的离心率为eq \r(3),则C的渐近线方程为________.
答案 y=±eq \r(2)x
解析 由双曲线的方程eq \f(x2,n)-eq \f(y2,4-n)=1知,双曲线的焦点在x轴上,∴eq \f(n+4-n,n)=(eq \r(3))2=3,
∴n=eq \f(4,3),∴a2=eq \f(4,3),b2=4-eq \f(4,3)=eq \f(8,3),从而双曲线的渐近线方程是y=±eq \r(2)x.
解题要点 1.已知双曲线方程eq \f(x2,a2)-eq \f(y2,b2)=1,求渐近线时可直接将1换为0,解方程eq \f(x2,a2)-eq \f(y2,b2)=0求出渐近线.
2.双曲线的离心率与渐近线方程之间有着密切的联系,二者之间可以互求.已知渐近线方程时,可得eq \f(b,a)的值,于是e2=eq \f(c2,a2)=eq \f(a2+b2,a2)=1+eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(b,a)))2,因此可求出离心率e的值;而已知离心率的值,也可求出渐近线的方程,即eq \f(b,a)=eq \r(e2-1).但要注意,当双曲线的焦点所在的坐标轴不确定时,上述两类问题都有两个解.
当堂练习
1.(2015广东理)已知双曲线C:eq \f(x2,a2)-eq \f(y2,b2)=1的离心率e=eq \f(5,4),且其右焦点为F2(5,0),则双曲线C的方程为________.
答案 eq \f(x2,16)-eq \f(y2,9)=1
解析 因为所求双曲线的右焦点为F2(5,0)且离心率为e=eq \f(c,a)=eq \f(5,4),所以c=5,a=4,b2=c2-a2=9,所以所求双曲线方程为eq \f(x2,16)-eq \f(y2,9)=1.
2.(2015安徽文)下列双曲线中,渐近线方程为y=±2x的是________.
①x2-eq \f(y2,4)=1 ②eq \f(x2,4)-y2=1 ③x2-eq \f(y2,2)=1 ④eq \f(x2,2)-y2=1
答案 ①
解析 由双曲线渐近线方程的求法知;双曲线x2-eq \f(y2,4)=1的渐近线方程为y=±2x,故选①.
3. (2015福建理)若双曲线E:eq \f(x2,9)-eq \f(y2,16)=1的左、右焦点分别为F1,F2,点P在双曲线E上,且|PF1|=3,则|PF2|等于________.
答案 9
解析 由双曲线定义||PF2|-|PF1||=2a,∵|PF1|=3,∴P在左支上,∵a=3,∴|PF2|-|PF1|=6,∴|PF2|=9.
4.(2015山东文)过双曲线C:eq \f(x2,a2)-eq \f(y2,b2)=1(a>0,b>0)的右焦点作一条与其渐近线平行的直线,交C于点P.若点P的横坐标为2a,则C的离心率为________.
答案 2+eq \r(3)
解析 把x=2a代入eq \f(x2,a2)-eq \f(y2,b2) =1;得y=±eq \r(3)b.
不妨取P(2a,-eq \r(3)b).又∵双曲线右焦点F2的坐标为(c,0),
∴kF2P=eq \f(\r(3)b,c-2a).由题意,得eq \f(\r(3)b,c-2a)=eq \f(b,a).
∴(2+eq \r(3))a=c.∴双曲线C的离心率为e=eq \f(c,a)=2+eq \r(3).
5.(2015北京文)已知(2,0)是双曲线x2-eq \f(y2,b2)=1(b>0)的一个焦点,则b=________.
答案 eq \r(3)
解析 由题意:c=2,a=1,由c2=a2+b2.得b2=4-1=3,所以b=eq \r(3).
课后作业
填空题
1. (2015天津文)已知双曲线eq \f(x2,a2)-eq \f(y2,b2)=1(a>0,b>0 )的一个焦点为F(2,0),且双曲线的渐近线与圆(x-2)2+y2=3相切,则双曲线的方程为________.
答案 x2-eq \f(y2,3)=1
2.(2015湖南文)若双曲线eq \f(x2,a2)-eq \f(y2,b2)=1的一条渐近线经过点(3,-4),则此双曲线的离心率为________.
答案 eq \f(5,3)
解析 由条件知y=-eq \f(b,a)x过点(3,-4),∴eq \f(3b,a)=4,
即3b=4a,∴9b2=16a2,∴9c2-9a2=16a2,∴25a2=9c2,∴e=eq \f(5,3).
3.(2015新课标II理)已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,且顶角为120°,则E的离心率为________.
答案 eq \r(2)
解析 如图,设双曲线E的方程为eq \f(x2,a2)-eq \f(y2,b2)=1(a>0,b>0),则|AB|=2a,由双曲线的对称性,可设点M(x1,y1)在第一象限内,过M作MN⊥x轴于点N(x1,0),∵△ABM为等腰三角形,且∠ABM=120°,∴|BM|=|AB|=2a,∠MBN=60°,
∴y1=|MN|=|BM|sin∠MBN=2asin 60°=eq \r(3)a,x1=|OB|+|BN|=a+2acs 60°=2a.将点M(x1,y1)的坐标代入eq \f(x2,a2)-eq \f(y2,b2)=1,可得a2=b2,∴e=eq \f(c,a)=eq \r(\f(a2+b2,a2))=eq \r(2).
4.已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于eq \f(3,2),则C的方程是________.
答案 eq \f(x2,4)-eq \f(y2,5)=1
解析 由曲线C的右焦点为F(3,0),知c=3.由离心率e=eq \f(3,2),知eq \f(c,a)=eq \f(3,2),则a=2,
故b2=c2-a2=9-4=5,所以双曲线C的方程为eq \f(x2,4)-eq \f(y2,5)=1.
5.已知双曲线C:eq \f(x2,a2)-eq \f(y2,b2)=1(a>0,b>0)的离心率为eq \f(\r(5),2),则C的渐近线方程为________.
答案 y=±eq \f(1,2)x
解析 ∵e=eq \f(c,a)=eq \f(\r(5),2),∴e2=eq \f(c2,a2)=eq \f(a2+b2,a2)=eq \f(5,4).∴a2=4b2,eq \f(b,a)=eq \f(1,2).∴渐近线方程为y=±eq \f(b,a)x=±eq \f(1,2)x.
6.(2015新课标Ⅰ理)已知M(x0,y0)是双曲线C:eq \f(x2,2)-y2=1上的一点,F1,F2是C的两个焦点,若eq \(MF1,\s\up6(→))·eq \(MF2,\s\up6(→))<0,则y0的取值范围是________.
答案 eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(\r(3),3),\f(\r(3),3)))
解析 由双曲线方程可求出F1,F2的坐标,再求出向量eq \(MF1,\s\up6(→)),eq \(MF2,\s\up6(→)),然后利用向量的数量积公式求解.
由题意知a=eq \r(2),b=1,c=eq \r(3),∴F1(-eq \r(3),0),F2(eq \r(3),0),
∴eq \(MF1,\s\up6(→))=(-eq \r(3)-x0,-y0),eq \(MF2,\s\up6(→))=(eq \r(3)-x0,-y0).
∵eq \(MF1,\s\up6(→))·eq \(MF2,\s\up6(→))<0,∴(-eq \r(3)-x0)(eq \r(3)-x0)+yeq \\al(2,0)<0,
即xeq \\al(2,0)-3+yeq \\al(2,0)<0.
∵点M(x0,y0)在双曲线上,∴eq \f(x\\al(2,0),2)-yeq \\al(2,0)=1,即xeq \\al(2,0)=2+2yeq \\al(2,0),
∴2+2yeq \\al(2,0)-3+yeq \\al(2,0)<0,∴-eq \f(\r(3),3)
答案 ±1
解析 双曲线eq \f(x2,a2)-eq \f(y2,b2)=1的右焦点F(c,0),左、右顶点分别为A1(-a,0),A2(a,0),易求Beq \b\lc\(\rc\)(\a\vs4\al\c1(c,\f(b2,a))),Ceq \b\lc\(\rc\)(\a\vs4\al\c1(c,-\f(b2,a))),则kA2C=eq \f(\f(b2,a),a-c),kA1B=eq \f(\f(b2,a),a+c),又A1B与A2C垂直,
则有kA1B·kA2C=-1,即eq \f(\f(b2,a),a+c)·eq \f(\f(b2,a),a-c)=-1,
∴eq \f(\f(b4,a2),c2-a2)=1,∴a2=b2,即a=b,∴渐近线斜率k=±eq \f(b,a)=±1.
8.(2015新课标II文)已知双曲线过点(4,eq \r(3)),且渐近线方程为y=±eq \f(1,2)x,则该双曲线的标准方程为________.
答案 eq \f(x2,4)-y2=1
解析 由双曲线渐近线方程为y=±eq \f(1,2)x,可设该双曲线的标准方程为eq \f(x2,4)-y2=λ(λ≠0),已知该双曲线过点(4,eq \r(3)),所以eq \f(42,4)-(eq \r(3))2=λ,即λ=1,故所求双曲线的标准方程为eq \f(x2,4)-y2=1.
9. (2015天津文)双曲线eq \f(x2,2)-y2=1的焦距是______,渐近线方程是________________.
答案 2eq \r(3) y=±eq \f(\r(2),2)x
解析 由双曲线方程得a2=2,b2=1,∴c2=3,∴焦距为2eq \r(3),渐近线方程为y=±eq \f(\r(2),2)x.
10.(2015湖南理)设F是双曲线C:eq \f(x2,a2)-eq \f(y2,b2)=1的一个焦点,若C上存在点P,使线段PF的中点恰为其虚轴的一个端点,则C的离心率为________.
答案 eq \r(5)
解析 不妨设F(c,0),则由条件知P(-c,±2b),代入eq \f(x2,a2)-eq \f(y2,b2)=1得eq \f(c2,a2)=5,∴e=eq \r(5).
11.(2015新课标Ⅰ文)已知F是双曲线C:x2-eq \f(y2,8)=1的右焦点,P是C的左支上一点,A(0,6eq \r(6)).当△APF周长最小时,该三角形的面积为________.
答案 12eq \r(6)
解析 设左焦点为F1,|PF|-|PF1|=2a=2,
∴|PF|=2+|PF1|,△APF的周长为|AF|+|AP|+|PF|=|AF|+|AP|+2+|PF1|,△APF周长最小即为|AP|+|PF1|最小,当A、P、F1在一条直线时最小,过AF1的直线方程为eq \f(x,-3)+eq \f(y,6\r(6))=1.与x2-eq \f(y2,8)=1联立,解得P点坐标为(-2,2eq \r(6)),此时S==12eq \r(6).
二、解答题
12.已知椭圆D:eq \f(x2,50)+eq \f(y2,25)=1与圆M:x2+(y-5)2=9,双曲线G与椭圆D有相同焦点,它的两条渐进线恰好与圆M相切,求双曲线G的方程.
解析 椭圆D的两个焦点为F1(-5,0),F2(5,0),∴双曲线中心在原点,焦点在x轴上,且c=5.
设双曲线G的方程为eq \f(x2,a2)-eq \f(y2,b2)=1(a>0,b>0),
∴渐近线方程为bx±ay=0且a2+b2=25,
又圆心M(0,5)到两条渐近线的距离为r=3.
∴eq \f(|5a|,\r(b2+a2))=3,得a=3,b=4,
∴双曲线G的方程为eq \f(x2,9)-eq \f(y2,16)=1.
13.已知双曲线关于两坐标轴对称,且与圆x2+y2=10相交于点P(3,-1),若此圆过点P的切线与双曲线的一条渐近线平行,求此双曲线的方程.
解析 切点为P(3,-1)的圆x2+y2=10的切线方程是3x-y=10.
∵双曲线的一条渐近线与此切线平行,且双曲线关于两坐标轴对称,
∴两渐近线方程为3x±y=0.
设所求双曲线方程为9x2-y2=λ(λ≠0).
∵点P(3,-1)在双曲线上,代入上式可得λ=80,
∴所求的双曲线方程为eq \f(x2,\f(80,9))-eq \f(y2,80)=1.标准方程
eq \f(x2,a2)-eq \f(y2,b2)=1
(a>0,b>0)
eq \f(y2,a2)-eq \f(x2,b2)=1
(a>0,b>0)
图形
性
质
范围
x≥a或x≤-a,y∈R
x∈R,y≤-a或y≥a
对称性
对称轴:坐标轴 对称中心:原点
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
渐近线
y=±eq \f(b,a)x
y=±eq \f(a,b)x
离心率
e=eq \f(c,a),e∈(1,+∞),其中c=eq \r(a2+b2)
实虚轴
线段A1A2叫作双曲线的实轴,它的长|A1A2|=2a;线段B1B2叫作双曲线的虚轴,它的长|B1B2|=2b;a叫作双曲线的实半轴长,b叫作双曲线的虚半轴长
a、b、c
的关系
c2=a2+b2 (c>a>0,c>b>0)
艺术生高考数学专题讲义:考点42 椭圆: 这是一份艺术生高考数学专题讲义:考点42 椭圆,共10页。试卷主要包含了椭圆的概念,椭圆的标准方程和几何性质,点P和椭圆的关系,椭圆中的弦长公式,椭圆中点弦有关的结论,设F1,F2分别是椭圆C,已知椭圆E等内容,欢迎下载使用。
艺术生高考数学专题讲义:考点43 双曲线: 这是一份艺术生高考数学专题讲义:考点43 双曲线,共8页。试卷主要包含了双曲线的概念,双曲线的标准方程和几何性质,双曲线与椭圆的区别,过双曲线C,已知M是双曲线C,设F是双曲线C等内容,欢迎下载使用。
艺术生高考数学专题讲义:考点42 椭圆: 这是一份艺术生高考数学专题讲义:考点42 椭圆,共10页。试卷主要包含了椭圆的概念,椭圆的标准方程和几何性质,点P和椭圆的关系,椭圆中的弦长公式,椭圆中点弦有关的结论,设F1,F2分别是椭圆C,已知椭圆E等内容,欢迎下载使用。












