人教版九年级上册21.1 一元二次方程优秀ppt课件

这是一份人教版九年级上册21.1 一元二次方程优秀ppt课件，文件包含人教版数学九年级上册211《一元二次方程》课件pptx、人教版数学九年级上册211《一元二次方程》教案docx等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

一元二次方程的概念，与得出一元一次方程的概念过程类似，教材先给出计算满足条件的正方形面积、计算满足条件的参赛队数等实际问题，用方程的思想建立数学模型，通过观察方程的特点，归纳、总结得到一元二次方程的概念。根据一元二次方程的概念，教材给出其一般形式为：ax2+bx+c=0（a≠0），其中二次项系数、一次项系数、常数项分别为：a、b、c，需注意二次项系数不能为0的原因及系数前的符号问题。基于以上分析，确定本节课的教学重点为：通过一元一次方程的概念，类比得出一元二次方程的概念。
1.理解一元二次方程的概念，根据一元二次方程的一般形式，确定各项系数.2.灵活应用一元二次方程概念解决有关问题.3.理解一元二次方程解（根）的概念，并能解决相关问题.
设计一座2m高的人体雕像，雕像上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感.按此比例，如果雕像的高为2m，那么它的下部应设计为多高？
雕像上部的高度AC，下部的高度BC的关系：
设雕像下部高 x m，于是得方程：
整理得：x2＋2x–4=0 ①
跟我们学过的一次方程一样吗？
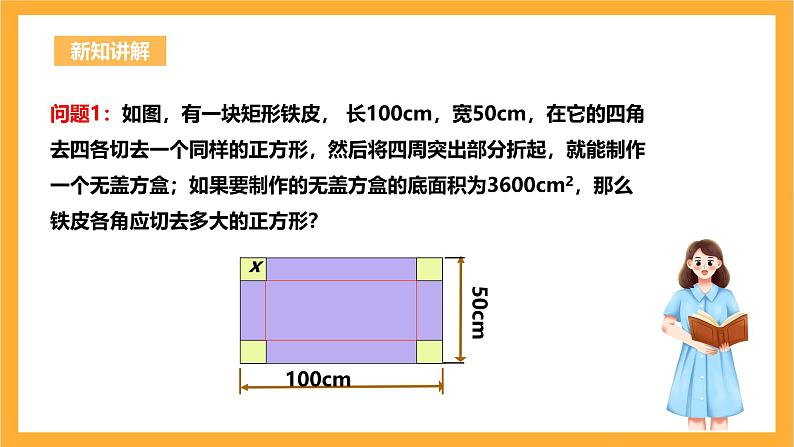
问题1：如图，有一块矩形铁皮， 长100cm，宽50cm，在它的四角去四各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒；如果要制作的无盖方盒的底面积为3600cm2，那么铁皮各角应切去多大的正方形？
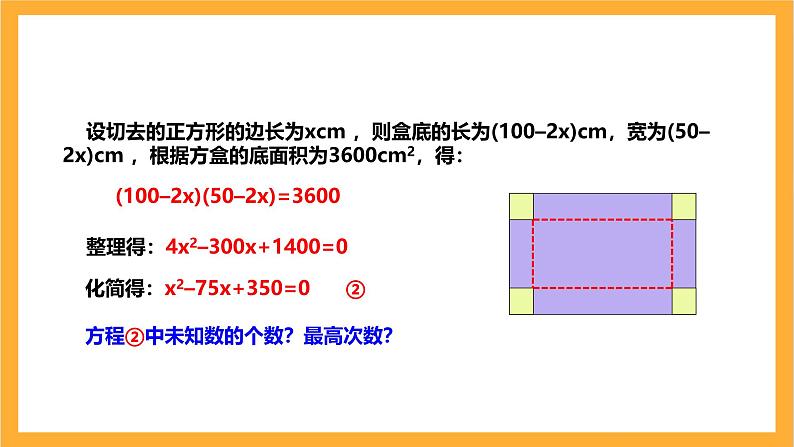
(100–2x)(50–2x)=3600
整理得：4x2–300x+1400=0
化简得：x2–75x+350=0 ②
设切去的正方形的边长为xcm ，则盒底的长为(100–2x)cm，宽为(50–2x)cm ，根据方盒的底面积为3600cm2，得：
方程②中未知数的个数？最高次数？
问题2: 要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，比赛组织者应邀请多少个队参赛？
分析:全部比赛共 4×7=28场
设应邀请x个队参赛,每个队要与其他 个队各赛一场。
由于甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛，即全部比赛共_____________场
方程③中未知数的个数？最高次数？
x2–75x+350=0 ②
观察下列各方程有什么共同点？
x2＋2x–4=0 ①
讨论：观察上述方程，它们与一元一次方程、二元一次方程、分式方程分别有什么不同点？
总结：（１）这些方程的两边都是______，（２）方程中只含有____未知数，未知数的最高次数是___.（3）这些方程是__________________
ax 2 + bx + c = 0（a≠0）
一元二次方程组概念：只含有_______未知数（元）， 并且未知数最高次数是_____， 等号两边都是________， 这样的方程叫一元二次方程。
一元二次方程的一般形式为____________________________________________。
使方程左右两边相等的未知数的值就是这个一元二次方程的解，一元二次方程的解也叫做一元二次方程的根.
例 将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式，并写出其中的二次项系数、一次项系数和常数项．
解：去括号，得 3x2–3x=5x+10 移项，合并同类项，得一元二次方程的一般形式 3x2–8x–10=0. 二次项系数为3，一次项系数为-8，常数项为-10．
1.判断下列方程是否为一元二次方程？ (1)x2+x=36 (2)x3+x2=36 (3)x+3y=36 (4)x2=0 (5)4x2=9 (6)(x+2)2=(x-1)2
x2-2x-168=0
x2-20x+50=0
【知识技能类作业】必做题：
3.若一元二次方程2x2+(2k+1)x-(4k-1)=0的二次项系数、一次项系数、常数项的和是0,则k=___.4.方程2x2=-8化成一般形式后，二次项系数为___，一次项系数为___,常数项为_____.
5.若x=2是方程x2-4mx+2m2=0的一个根，求代数式3（m-2）2-1的值.
【知识技能类作业】选做题：
解：依题意得：22-4m×2+2m2=0， 整理得：（m-2）2=3， 所以3（m-2）2-1=3×32-1=26，即3（m-2）2-1=26．
6．若关于x的方程（k+3）x2－kx＋1＝0是一元二次方程，求k的取值范围。
解：∵方程（k+3）x2－kx＋1＝0是一元二次方程，∴ k+3≠0∴ k≠-3
7．已知关于x的方程(2k＋1)x2＋4kx＋k－1＝0，问：（1）k为何值时，此方程是一元一次方程？（2）k为何值时，此方程是一元二次方程？并写出这个一元二次方程的二次项系数、一次项系数及常数项．
是整式方程；含一个未知数；（一元）最高次数是2.（二次）
ax2+bx+c=0 (a ≠0) 其中(a≠0)是一元二次方程的必要条件；
使方程左右两边相等的未知数的值.
等号两边都是整式，只含一个未知数且未知数的最高次数是2的方程
1.一元二次方程概念：
2.一元二次方程的一般形式：
1. 若x=1是方程 x2-2x+a=0 的根，则 a= ____________．2. 关于x的方程（2a－4）x2－2x+a=0, 1）在什么条件下此方程为一元二次方程？2）在什么条件下此方程为一元一次方程？
解：(1)由题意得：2a-4≠0，即a≠2时，方程为一元二次方程(2)当2a-4=0，即a=2时，方程为一元一次方程
3. a为何值时，方程(a-1)x︱a︱+1-2x-7=0为一元二次方程？4. 若a是一元二次方程x2+2x-3=0的一个根，则2a2+4a的值是___________．
5.（1）当m为何值时，关于x的方程(m2-1) x2+mx-2=0是一元二次方程？（2）已知关于x的一元二次方程(m2-1) x2+mx-3-m=0有一个根是0，求m的值．（3）在第（2）题中，如果要使已知方程有一个根是1，那么m应该等于什么数？
解: （1）当m2-1≠0，即m≠±1时，方程是一元二次方程。（2）由题意得：-3-m=0，即m=-3(3)当x=1得：m2-1+m-3-m=0解得：m=±2