人教版九年级上册21.3 实际问题与一元二次方程完整版ppt课件

这是一份人教版九年级上册21.3 实际问题与一元二次方程完整版ppt课件，文件包含人教版数学九年级上册213《实际问题与一元二次方程》课件pptx、人教版数学九年级上册213《实际问题与一元二次方程》教案docx等2份课件配套教学资源，其中PPT共30页， 欢迎下载使用。

一元二次方程是中学数学的主要内容，在初中数学中占有重要地位，其中一元二次方程的实际应用在初中数学应用问题中极具代表性，它是一元一次方程应用的继续，又是二次函数学习的基础，它是研究现实世界数量关系和变化规律的重要模型。本节课以一元二次方程解决的实际问题为载体，通过对它的进一步学习和研究体现数学建模的过程帮助学生增强应用认识。
1.根据实际问题中的数量关系，正确列出一元二次方程。2.通过列方程解应用题体会一元二次方程在实际生活中的应用，经历将实际问题转化为数学问题的过程，提高数学应用意识。
【提问】回顾列方程解决实际问题的基本步骤?
1）审：分清已知未知，明确数量关系；
5）验：根据实际验结果；
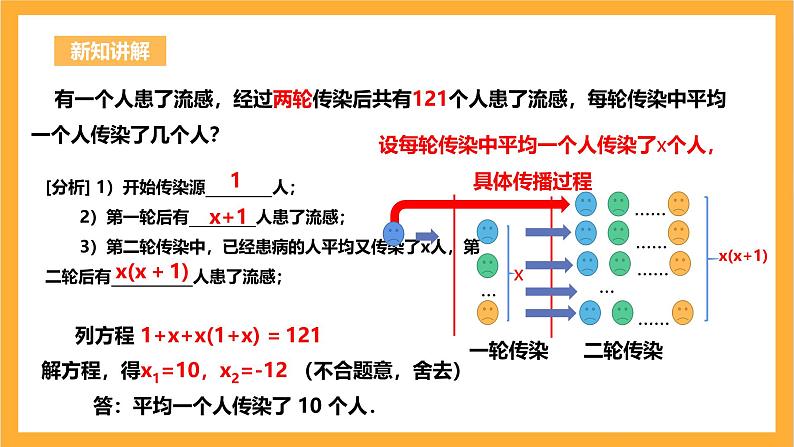
有一个人患了流感，经过两轮传染后共有121个人患了流感，每轮传染中平均一个人传染了几个人？
[分析] 1）开始传染源_________人； 2）第一轮后有_________人患了流感； 3）第二轮传染中，已经患病的人平均又传染了x人，第二轮后有___________人患了流感；
设每轮传染中平均一个人传染了x个人，
列方程 1+x+x(1+x) = 121
　　答：平均一个人传染了 10 个人．
解方程，得x1=10，x2=-12 （不合题意，舍去）
【问题】如果按照这样的传播速度，第三轮传染过后总共会有多少人得流感？
[分析]经过两轮传染后共有_______个人患了流感,平均每轮传染________人，则第三轮有___________人患了流感。
121+121×10 = 1 331（人）
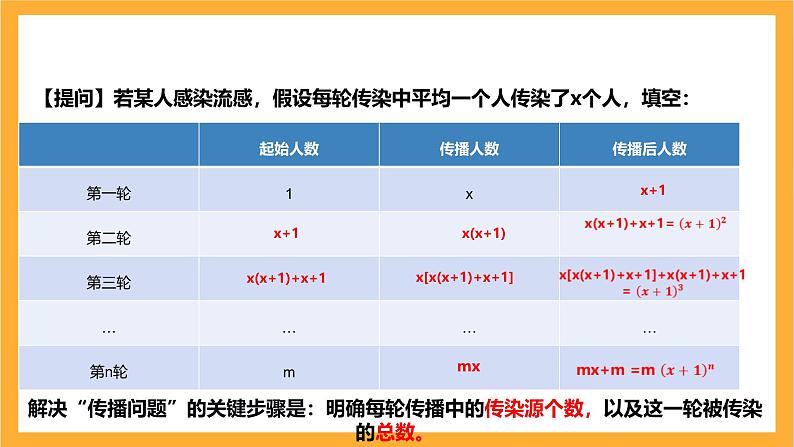
【提问】若某人感染流感，假设每轮传染中平均一个人传染了x个人，填空：
x[x(x+1)+x+1]
解决“传播问题”的关键步骤是：明确每轮传播中的传染源个数，以及这一轮被传染的总数。
例、某种流感病毒，若有一人患了这种流感，则在每轮传染中一人将平均传染x人．(1)现有一人患上这种流感，求第一轮传染后患病的人数（用含x的代数式表示）；(2)在进入第二轮传染前，有两位患者被及时隔离并治愈，问第二轮传染后患病的人数会有21人吗？
【提问】什么是下降额？下降率如何计算？
下降额=下降前的量-下降后的量
增长额=增长后的量-增长前的量
【提问】什么是增长额？增长率如何计算？
两年前生产1t甲种药品的成本是5000元，生产1t乙种药品的成本是6000元，随着生产技术的进步，现在生产1t甲种药品的成本是3000元，生产1t乙种药品的成本是3600元，哪种药品成本的年平均下降率较大？
乙种药品成本的年平均下降额为（6000-3600）÷2=1200（元）．
甲种药品成本的年平均下降额为（5000-3000）÷2=1000（元），
显然，乙种药品成本的年平均下降额较大，但是，年平均下降额（元）不等同于年平均下降率（百分数）。
解：设甲种药品成本的年平均下降率为 x　　一年后甲种药品成本为__________________元，　　两年后甲种药品成本为____________ 元．
答：甲种药品成本的年平均下降率为22.5%
【补充】下降率是用减少的数除以原数，则所得结果必定小于1，因此不能大于或等于1。
解：设乙种药品成本的年平均下降率为 y　　一年后乙种药品成本为____________ 元，　　两年后乙种药品成本为____________ 元．
答：乙种药品成本的年平均下降率为22.5%
【问题】经过计算，你能得出什么结论？
【问题】成本下降额大的药品，它的成本下降率一定也大吗？
【问题】应怎样全面地比较几个对象的变化状况？
成本下降额表示绝对变化量，成本下降率表示相对变化量，两者兼顾才能全面比较对象的变化状况。
两种药品成本的年平均下降率相等
成本下降额较大的产品，其成本下降率不一定较大。
要设计一本书的封面，封面长 27 cm，宽 21 cm，正中央是一个与整个封面长宽比例相同的矩形，如果要使四周的彩色边衬所占面积是封面面积的四分之一，上、下边衬等宽，左、右边衬等宽，应如何设计四周边衬的宽度？
【分析】封面的长宽之比是9∶7，中央的矩形的长宽之比也应是9∶7。
设中央的矩形的长和宽分别是 9a cm和 7a cm，由此得上、下边衬与左、右边衬的宽度之比是：
整理,得：16y 2 - 48y + 9 = 0
答：上、下边衬的宽度为1.8cm，左、右边衬的宽度为1.4cm
所以9y=1.8 cm，7y=1.4 cm
【提问】为什么舍去2.8？请说明原因？
例、如图,在一块长为 92m ,宽为 60m 的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为 885m2 的 6 个小矩形，水渠应挖多宽？
解：设水渠的宽应挖 x m .92×60 - 92x - 2×60x+ 2x2 = 6×885
解得 x1=105(舍去），x2=1答：水渠应挖1米宽。
【知识技能类作业】必做题：
3.如图，准备在一块长为30米，宽为24米的长方形花圃内修建四条宽度相等，且与各边垂直的小路，四条小路围成的中间部分恰好是一个正方形，且边长是小路宽度的4倍，若四条小路所占面积为80平方米，则小路的宽度为_____米．
【知识技能类作业】选做题：
5. 如图，某农户准备建一个长方形养鸡场，养鸡场的一边靠墙，若墙长为18m，另三边用竹篱笆围成，篱笆总长35m，围成长方形的养鸡场四周不能有空隙．（1）要围成养鸡场的面积为150m2，则养鸡场的长和宽各为多少？（2）围成养鸡场的面积能否达到200m2？请说明理由．
解：1）设养鸡场的宽为xm，根据题意得：x（35﹣2x）＝150，解得：x1＝10，x2＝7.5，当x1＝10时，35﹣2x＝15＜18，当x2＝7.5时35﹣2x＝20＞18，（舍去），则养鸡场的宽是10m，长为15m．
2）设养鸡场的宽为xm，根据题意得：x（35﹣2x）＝200，整理得：2x2﹣35x+200＝0，△＝（﹣35）2﹣4×2×200＝1225﹣1600＝﹣375＜0，因为方程没有实数根，所以围成养鸡场的面积不能达到200m2．
6．“杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标，第三阶段实现水稻亩产量1008公斤的目标．（1）如果第二阶段、第三阶段亩产量的增长率相同，求亩产量的平均增长率；（2）按照（1）中亩产量增长率，科研团队期望第四阶段水稻亩产量达到1200公斤，请通过计算说明他们的目标能否实现．
实际问题与一元二次方程
审，设，列，解，检验，答
1、传播问题2、平均增长率问题3、几何面积问题
21.3实际问题与一元二次方程
列一元二次方程解应用题的步骤：①审题，明确已知量和未知量，找出等量关系式；②设未知数，比较不同的未知量，找到最合适的未知量；③列方程，合理排布等量关系式；④解方程，利用合适的方法解方程；⑤检验并写出答案，务必进行验根，并进行回答。
1.电影《长津湖》票房最终突破了57亿元．第一天票房约4.1亿元，三天后票房累计总收入达14.22亿元，如果第二天，第三天票房收入按相同的增长率增长，增长率设为x．则可列方程为（　　）A．4.1(1+x)＝14.22 B．4.1(1+x)²＝14.22C．4.1+4.1(1+x)²＝14.22 D．4.1+4.1(1+x)+4.1(1+x)²＝14.222.如图，一块长和宽分别为30cm和20cm的矩形铁皮，要在它的四角截去四个边长相等的小正方形，使它的侧面积为272cm²，则截去的正方形的边长是（　　）A．4cmB．8.5cmC．4cm或8.5cmD．5cm或7.5cm
4.山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：1）每千克核桃应降价多少元？2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？