初中数学人教版九年级上册22.1.1 二次函数完整版ppt课件

这是一份初中数学人教版九年级上册22.1.1 二次函数完整版ppt课件，文件包含人教版数学九年级上册2214《二次函数yax2+bx+c的图象与性质》课件pptx、人教版数学九年级上册2214《二次函数yax2+bx+c的图象与性质》教案docx等2份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

1.通过图象了解二次函数y＝ax2＋bx＋c的性质，体会数形结合的思想．2.会用待定系数法确定二次函数y＝ax2＋bx＋c的解析式．3.通过确定二次函数解析式的过程，体会综合运用函数解析式和过函数图象上的点的数形结合思想．
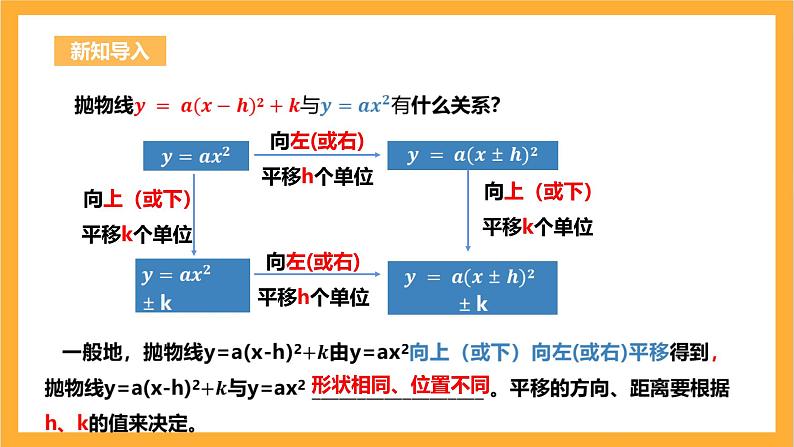
向左(或右)平移h个单位
向上（或下）平移k个单位
你知道是怎样配方的吗？
3.“化”：化成顶 点式.
1. “提”：提出二次项系数；
2.“配”：括号内配成完全平方式；
向右平移6个单位再向上平移3个单位
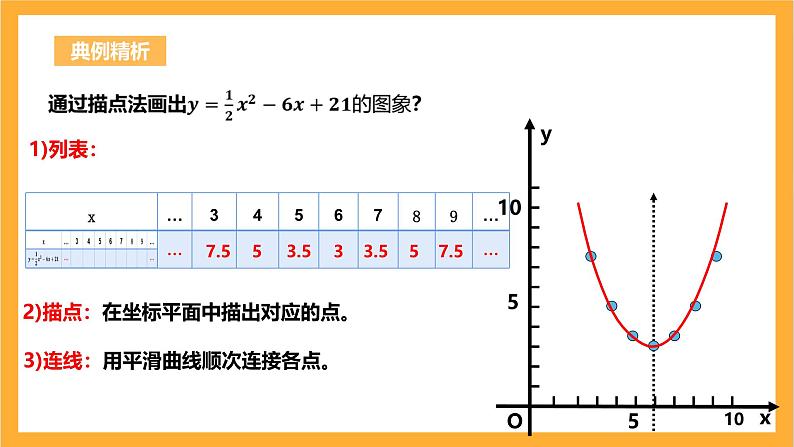
2)描点：在坐标平面中描出对应的点。
3)连线：用平滑曲线顺次连接各点。
求二次函数y=ax2＋bx＋c的顶点式？
配方：加上再减去一次项系数绝对值一半的平方
整理：前三项化为平方形式，后两项合并同类项
例、把下面二次函数的一般式化成顶点式： y＝2x2－5x＋3.
已知一次函数图象上的几个点可以求出它的解析式？利用了怎样的方法？
已知一次函数图象上的两个点的坐标就可以通过待定系数法求它的解析式。
若二次函数经过(-1,10)、(1,4)、(2,7)三个点，能求出二次函数的解析式吗？
已知抛物线过三点，求其解析式，可采用一般式；而用一般式求待定系数要经历以下四步：第一步：设一般式y＝ax2＋bx＋c；第二步：将三点的坐标分别代入一般式中，组成一个三元一 次方程组；第三步：解方程组即可求出a，b，c的值；第四步：写出函数解析式.
例、已知抛物线的顶点为(-1，-3),与y轴交点为(0，-5),求抛物线的解析式.
解：由题意可得，抛物线的顶点为(-1，-3)设所求二次函数为y＝a(x+1)2-3．∵函数图象经过点(0，-5)，∴a(0+1)2－3＝－5．解得a＝-2．所求二次函数是y＝-2(x+1)2－3．
【知识技能类作业】必做题：
1.对于二次函数y＝－14x2＋x－4，下列说法正确的是(　　)A．当x＞0时，y随x的增大而增大 B．当x＝2时，y有最大值－3C．图象的顶点坐标为(－2，－7) D．图象与x轴有两个交点2.如图，抛物线对应的函数解析式是(　　)A．y＝x2－x＋2 B．y＝－x2＋x＋2C．y＝x2＋x＋2 D．y＝－x2＋x－2
【知识技能类作业】选做题：
5.已知二次函数y＝ax2＋4x＋2的图象经过点A(3，－4)． (1)求a的值；
解：由题意得－4＝9a＋12＋2，解得a＝－2.
(2)求此抛物线的开口方向、顶点坐标和对称轴；
由(1)得二次函数为y＝－2x2＋4x＋2，可化为y＝－2(x－1)2＋4.故抛物线开口向下，顶点坐标为(1，4)，对称轴为直线x＝1.
(3)直接写出函数y随自变量增大而减小的x的取值范围．
7.如图，已知抛物线y＝－x2＋mx＋3与x轴交于A，B两点，与y轴交于点C，点B的坐标为(3，0)．(1)求m的值及抛物线的顶点坐标；(2)点P是抛物线对称轴l上的一个动点，当PA＋PC的值最小时， 求点P的坐标．
解：（1）把点B(3，0)的坐标代入y＝－x2＋mx＋3得: 0＝－32＋3m＋3， 解得m＝2， ∴y＝－x2＋2x＋3＝－(x－1)2＋4. ∴顶点坐标为(1，4)．
（2）如图，连接BC交抛物线的对称轴l于点P，则此时PA＋PC的值最小．
y=a(x-h)2+k
待定系数法求二次函数解析式
4.已知二次函数的图象经过点(0，3)，(－3，0)， (2，－5)，且 与x轴交于A，B两点．(1)试确定此二次函数的解析式．
(2)判断点P(－2，3)是否在这个二次函数的图象上．如果在，请求出△PAB的面积；如果不在，试说明理由．
5.如图，已知抛物线y＝ax2＋bx＋c与x轴交于点A(1，0)，B(3，0)，且过点C(0，－3)．(1)求抛物线的解析式和顶点坐标；(2)请你写出一种平移的方法，使平移后抛物线的顶点落在直线y＝－x上，并写出平移后抛物线的解析式．
解：(1)∵抛物线与x轴交于点A(1，0)，B(3，0)， ∴可设抛物线解析式为y＝a(x－1)(x－3)， 把(0，－3)代入得：3a＝－3，解得：a＝－1， 故抛物线的解析式为y＝－(x－1)(x－3)， 即y＝－x2＋4x－3， ∵y＝－x2＋4x－3＝－(x－2)2＋1， ∴顶点坐标为(2，1)．(2)先向左平移2个单位，再向下平移1个单位，得到的抛物 线的解析式为y＝－x2，平移后抛物线的顶点为(0，0)， 落在直线y＝－x上．