初中数学24.1.2 垂直于弦的直径公开课ppt课件

这是一份初中数学24.1.2 垂直于弦的直径公开课ppt课件，文件包含人教版数学九年级上册2412《垂直于弦的直径》课件pptx、人教版数学九年级上册2412《垂直于弦的直径》教学设计docx等2份课件配套教学资源，其中PPT共25页， 欢迎下载使用。

1.理解圆的轴对称性及垂径定理的推导，能初步应用垂径定理进行计算和证明；2.通过圆的对称性，培养学生对数学的审美观，并激发学生对数学的热爱.
中国汉代数学典籍《九章算术》勾股章所记载的“圆材埋壁”问题，原文：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，问径几何？”翻译：现有圆柱状的木材，埋在墙壁里。不知道其大小，于是用锯子（沿横截面）锯它，当量得深度为一寸的时候，锯开的宽度为一尺，问木材的直径是多少？（一尺等于十寸）用数学语言可表述为：“如图，在⊙O中，弦CD=10寸，弓形高AB=1寸，求直径的长。”
探究：剪一个圆形纸片，沿着它的任意一条直径对折，重复做几次，你发现了什么？由此你能得出什么结论？猜想：圆是轴对称图形，任何一条直径所在的直线都是圆的对称轴. 你能证明上述结论吗？
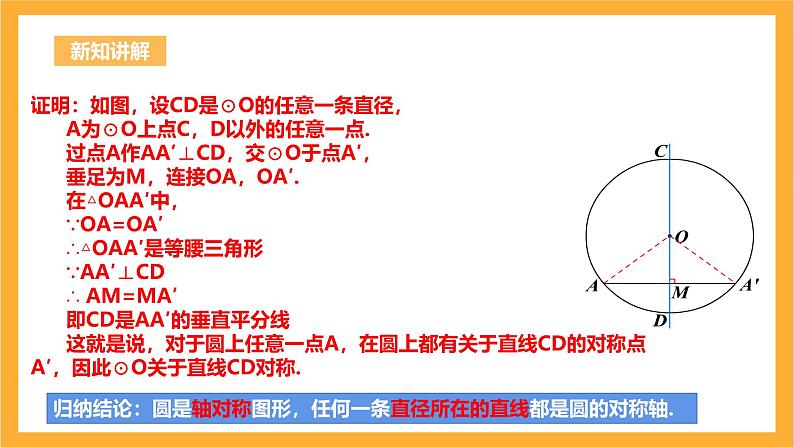
证明：如图，设CD是⊙O的任意一条直径， A为⊙O上点C，D以外的任意一点. 过点A作AA′⊥CD，交⊙O于点A′， 垂足为M，连接OA，OA′.   在△OAA′中，   ∵OA=OA′   ∴△OAA′是等腰三角形   ∵AA′⊥CD   ∴ AM=MA′   即CD是AA′的垂直平分线   这就是说，对于圆上任意一点A，在圆上都有关于直线CD的对称点A′，因此⊙O关于直线CD对称.  
归纳结论：圆是轴对称图形，任何一条直径所在的直线都是圆的对称轴.
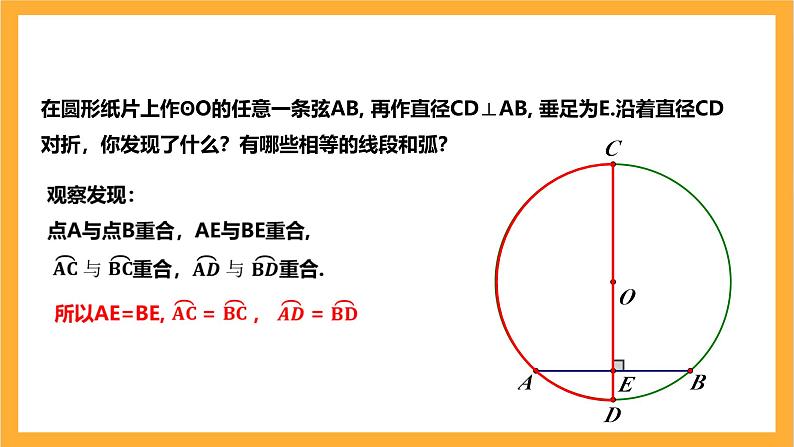
在圆形纸片上作ʘO的任意一条弦AB, 再作直径CD⊥AB, 垂足为E.沿着直径CD对折，你发现了什么？有哪些相等的线段和弧？
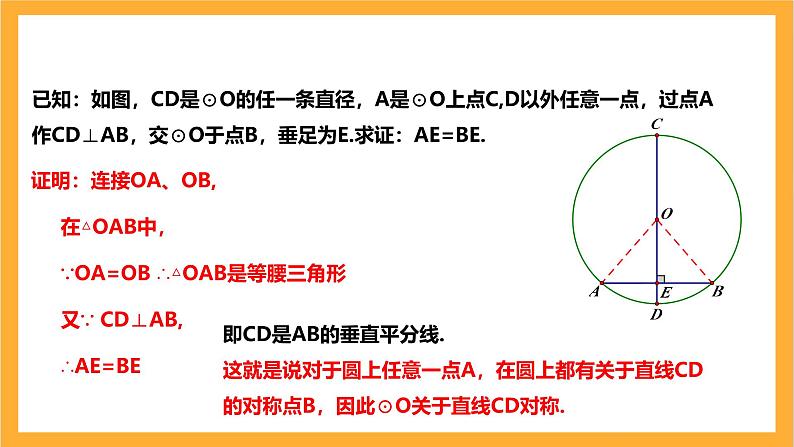
已知：如图，CD是⊙O的任一条直径，A是⊙O上点C,D以外任意一点，过点A作CD⊥AB，交⊙O于点B，垂足为E.求证：AE=BE.
证明：连接OA、OB, 在△OAB中， ∵OA=OB ∴△OAB是等腰三角形 又∵ CD⊥AB, ∴AE=BE
即CD是AB的垂直平分线.这就是说对于圆上任意一点A，在圆上都有关于直线CD的对称点B，因此⊙O关于直线CD对称.
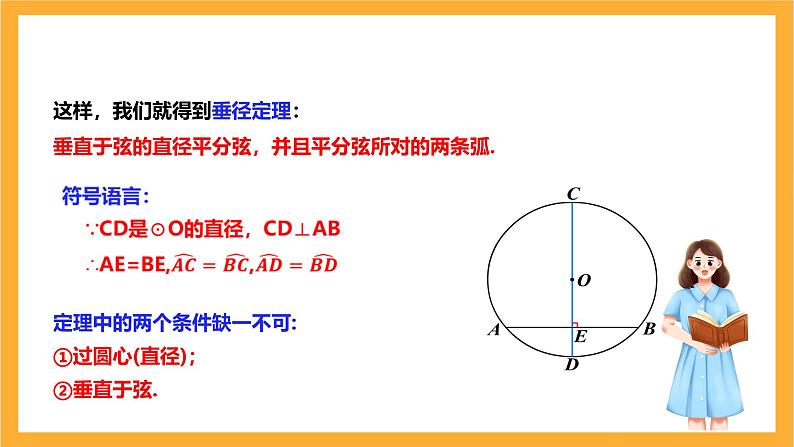
这样，我们就得到垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧.
定理中的两个条件缺一不可:①过圆心(直径)； ②垂直于弦.
CD是直径、AB是弦，CD⊥AB
①直径过圆心②垂直于弦
③平分弦④平分弦所对的优弧⑤平分弦所对的劣弧
将题设与结论调换过来，还成立吗？
① 直径过圆心 ③ 平分弦
② 垂直于弦④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
例2 赵州桥（如图）是我国隋代建造的石拱桥，距今约有1400年的历史，是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形，它的跨度（弧所对的弦的长）为37m，拱高（弧的中点到弦的距离）为7.23m，求赵州桥主桥拱的半径（结果保留小数点后一位）.
分析：解决此问题的关键是根据赵州桥的实物图画出几何图形.
在圆中有关弦长a,半径r, 弦心距d（圆心到弦的距离），弓形高h的计算题时，常常通过连半径或作弦心距构造直角三角形，利用垂径定理和勾股定理求解.
弦a，弦心距d，弓形高h，半径r之间有以下关系：
d+h=r
涉及垂径定理时辅助线的添加方法
【知识技能类作业】必做题：
4.如图，OE⊥AB于E，若⊙O的半径为10cm,OE=6cm,则AB= cm.
3.已知⊙O中，弦AB=8cm，圆心到AB的距离为3cm，则此圆的半径为 .
【知识技能类作业】选做题：
5.如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm.求⊙O的半径.
6.如图,射线PG平分∠EPF,O为射线PG上一点,以点O为圆心,5为半径作☉O分别与∠EPF的两边相交于点A,B和点C,D,连接OA,且OA∥PE.(1)求证:AP=AO;(2)若弦AB=8,求OP的长.
(1)证明:∵PG平分∠EPF,∴∠DPO=∠APO.∵AO∥PE,∴∠DPO=∠AOP, ∴∠APO=∠AOP,∴AP=AO.
一条直线满足:①过圆心;②垂直于弦; ③平分弦（不是直径）; ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论（“知二推三”）
垂直于弦的直径平分弦,并且平分弦所对的两条弧
两条辅助线：连半径，作弦心距
构造Rt△利用勾股定理计算或建立方程.
1.垂径定理：垂直于弦的直径平分弦,并且平分弦所对的两条弧
2.推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.
1．往直径为52cm的圆柱形容器内装入一些水以后，截面如图所示，若水面宽AB＝48cm，则水的最大深度为（　　）A．8cm B．10cm C．16cm D．20cm2.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？”意思是：今有一圆柱形木材，埋在墙壁中，不知其大小．用锯去锯这木材，锯口深ED＝1寸，锯道长AB＝1尺（1尺＝10寸）．问这根圆形木材的直径是　 　寸．
3.☉O的半径为13cm，AB、CD是☉O的两条弦，AB∥CD，AB=24cm，CD=10cm，求AB和CD之间的距离．
解：当弦AB和CD在圆心异侧时，过点0作OE⊥CD于点E,作OF⊥AB于点F,连结OA,OC. ∵AB＝24cm，CD＝10cm， ∴AF＝12cm，CE＝5cm， ∵OA＝OC＝13cm， ∴EO＝12cm，OF＝5cm， ∴EF＝OF＋OE＝17cm． ∴AB与CD之间的距离为7cm或17cm．
4.如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E.(1)当BC=1时,求线段OD的长.(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.