初中数学24.2.2 直线和圆的位置关系获奖课件ppt

这是一份初中数学24.2.2 直线和圆的位置关系获奖课件ppt，文件包含人教版数学九年级上册24223《直线与圆的位置关系》课件pptx、人教版数学九年级上册24223《直线与圆的位置关系》教学设计docx等2份课件配套教学资源，其中PPT共27页， 欢迎下载使用。

1 了解三角形内切圆、内心的概念，会作三角形内切圆；掌握切线长定理，并会用其解决有关问题．2 经历探索切线长定理的过程，体会应用内切圆相关知识解决问题，渗透转化思想和方程思想．
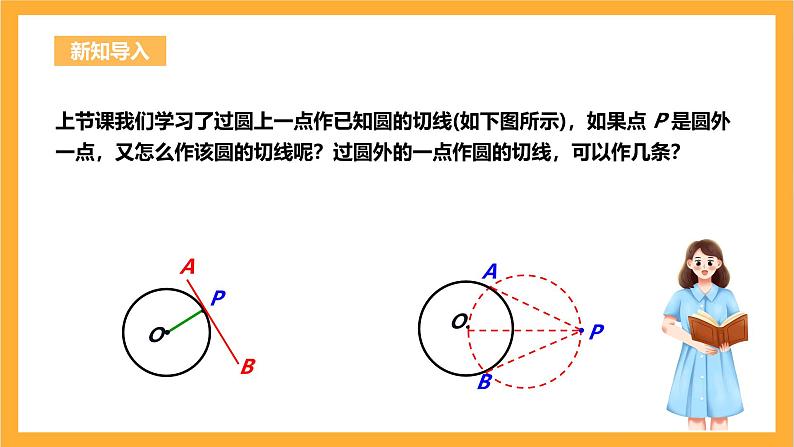
上节课我们学习了过圆上一点作已知圆的切线(如下图所示)，如果点 P 是圆外一点，又怎么作该圆的切线呢？过圆外的一点作圆的切线，可以作几条？
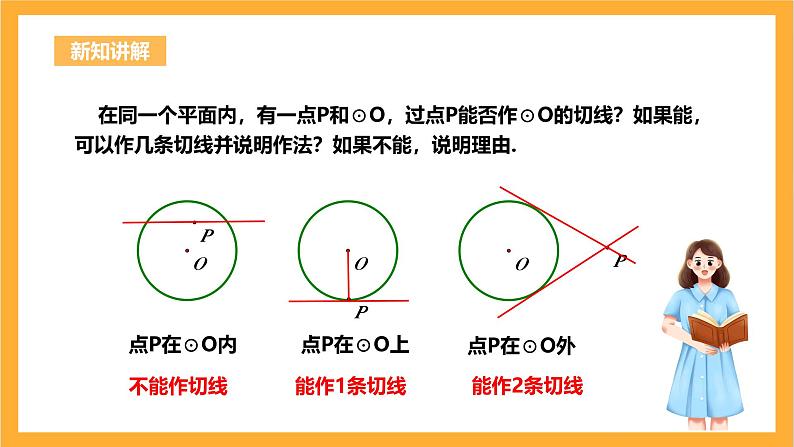
在同一个平面内，有一点P和⊙O，过点P能否作⊙O的切线？如果能，可以作几条切线并说明作法？如果不能，说明理由.
经过圆外一点的圆的切线上，这点和切点之间的线段的长叫做这点到圆的切线长．
①切线是直线，无法度量.
②切线长是切线上一条线段的长，即圆外一点与切点之间的距离，可以度量．
2.切线长与切线的区别：
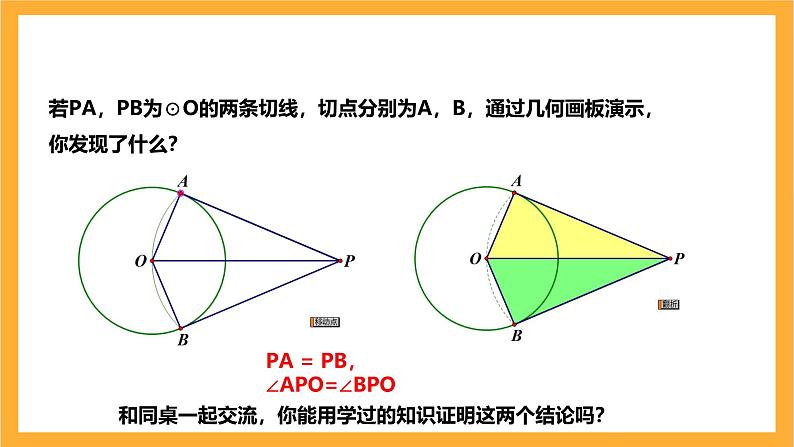
若PA，PB为⊙O的两条切线，切点分别为A，B，通过几何画板演示，你发现了什么？
PA = PB，∠APO=∠BPO
和同桌一起交流，你能用学过的知识证明这两个结论吗？
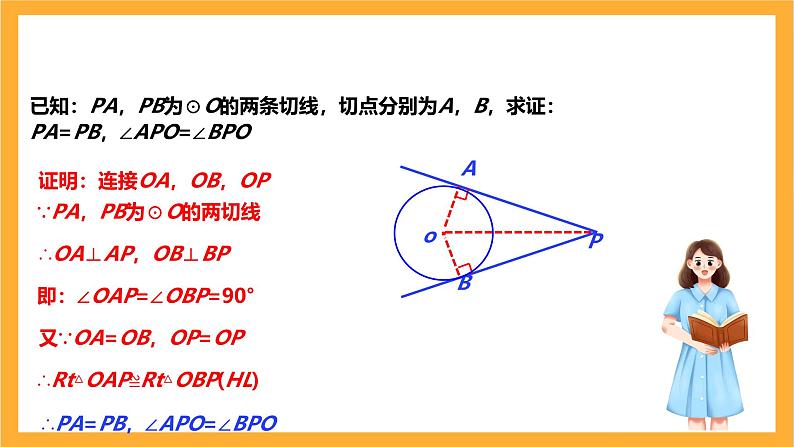
已知：PA，PB为⊙O的两条切线，切点分别为A，B，求证：PA=PB，∠APO=∠BPO
证明：连接OA，OB，OP
∵PA，PB为⊙O的两切线
即：∠OAP=∠OBP=90°
又∵OA=OB，OP=OP
∴Rt△OAP≌Rt△OBP(HL)
∴PA=PB，∠APO=∠BPO
∴OA⊥AP，OB⊥BP
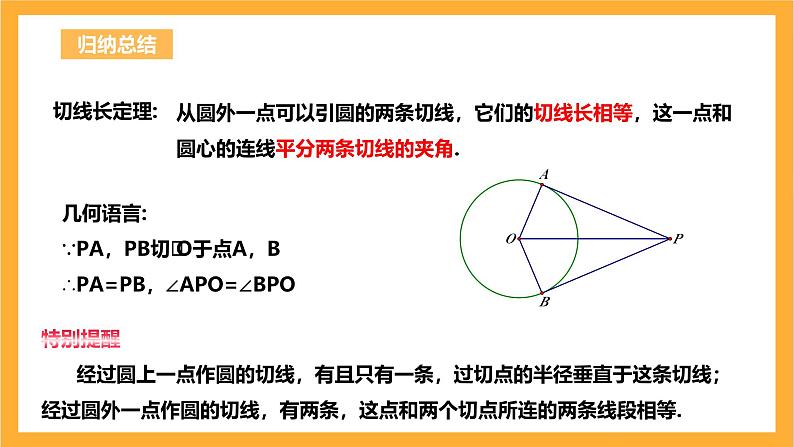
从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.
几何语言:∵PA，PB切⨀O于点A，B∴PA=PB，∠APO=∠BPO
特别提醒经过圆上一点作圆的切线，有且只有一条，过切点的半径垂直于这条切线；经过圆外一点作圆的切线，有两条，这点和两个切点所连的两条线段相等.
若连接两切点 A，B，AB 交 OP 于点 M. 你又能得出什么新的结论? 请给出证明.
解：OP 垂直平分 AB.
证明：∵ PA，PB 是 ⊙O 的切线，点 A，B 是切点，∴ PA = PB，∠OPA =∠OPB.∴ △PAB 是等腰三角形， PM 为顶角的平分线.∴ OP 垂直平分 AB.
如图是切线长定理的一个基本图形, 可以直接得到结论：(1)PO ⊥ AB；(2)AO ⊥ AP，BO ⊥ BP；(3)AP=BP；(4)∠ 1= ∠ 2= ∠ 3= ∠ 4； (5)AD=BD.
思考： 一张三角形的铁皮，如何在它上面截下一块圆形的用料，使截出的圆与三角形各边都相切？
问题1 圆心应满足什么条件？
圆心到三角形三条边的距离都等于半径
问题2 如何确定圆心与半径？
三角形三条角平分线的交点（圆心）到三边的距离（半径）相等
3.以O为圆心， OD为半径作圆.
1.作∠B和∠C的平分线BM和CN交于点O，
2.过点O作OD⊥BC于点D，
与三角形各边都相切的圆叫做三角形的内切圆，
这个三角形叫做这个圆的外切三角形，
⊙O是△ABC的内切圆，点O是△ABC的内心，△ABC是⊙O的外切三角形.
内切圆的圆心是三角形角平分线的交点，叫做三角形的内心。
三角形外心：三角形三边垂直平分线的交点。外心到三角形三个顶点的距离相等。
三角形内心：三角形三内角平分线的交点。内心到三角形三边的距离相等。
例2 如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=9，BC=14，CA=13.求AF、BD、CE的长.
解：设AF=x，则AE=x，CD=CE=AC-AE=13-x， BD=BF=AB-AF=9-x 由BD+CD=BC，可得(13-x)+(9-x)=14 解得 x=4 因此 AF=4，BD=5，CE=9.
【知识技能类作业】必做题：
1、如图，AB、AC是⊙O的两条切线，B、C是切点，若∠A=70°，则∠BOC的度数为（ ）A．130° B．120° C．110° D．100°2、如图，PA，PB分别与⊙O相切于A、B两点．直线EF切⊙O于C点，分别交PA、PB于E、F，且PA＝10．则△PEF的周长为（　　）A．10B．15C．20D．25
3.如图,△ABC的内切圆分别和BC,AC,AB切于D,E,F; 如果AF=2,BD=7,CE=4,则BC= ,AC= ，AB= . 4.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8cm,则△PDE的周长为______.
【知识技能类作业】选做题：
5.如图，△ABC中，∠B=43°，∠C=61 °，点I是△ABC的内心，求∠BIC的度数.
解：连接IB，IC.∵点I是△ABC的内心，∴BI，CI分别平分∠ABC，∠ACB.
6.如图，在△ABC中，I是内心，∠BAC的平分线和△ABC的外接圆相交于点D.求证：DI＝DB.
证明：连接BI.∵I是△ABC的内心，∴∠BAD=∠CAD，∠ABI=∠CBI.∵∠CBD=∠CAD，∴∠BAD=∠CBD.∵∠BID=∠BAD+∠ABI，∠IBD=∠CBI+∠CBD，∴∠BID=∠IBD. ∴BD=ID．
一、切线长定义二、切线长定理
1.下列说法正确的是(　　)A．过任意一点总可以作圆的两条切线B．圆的切线长就是圆的切线的长度C．过圆外一点所画的圆的两条切线长相等D．过圆外一点所画的圆的切线长一定大于圆的半径2.△ABC的内切圆⊙O与三边分别切于D、E、F三点，如图，已知AF=3,BD+CE=12,则△ABC的周长是 .
3.如图，⊙O是△ABC的内切圆，切点分别为D，E，F，∠B＝60°，∠C＝70°，求∠EDF的度数．
根据上述材料，解答下列问题：如图，在△ABC中，BC＝5，AC＝6，AB＝9（1）用海伦公式求△ABC的面积；（2）求△ABC的内切圆半径r．