重庆市梁平区2023年八年级数学第一学期期末联考模拟试题【含解析】

这是一份重庆市梁平区2023年八年级数学第一学期期末联考模拟试题【含解析】，共20页。试卷主要包含了计算的结果是等内容，欢迎下载使用。
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．已知一个多边形的每个内角都等于，则这个多边形一定是( )
A．七边形B．正七边形C．九边形D．不存在
2．如图，在△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线交AC，AD，AB于点E，O，F，则图中全等三角形的对数是（ ）
A．1对B．2对C．3对D．4对
3．《孙子算经》中有一道题，原文是：“今有木，不知长短.引绳度之，余绳四尺五寸；屈绳量之，不足一尺.木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问木长多少尺，设木长为尺，绳子长为尺，则下列符合题意的方程组是（ ）
A．B．C．D．
4．把分式方程转化为一元一次方程时，方程两边需同乘以( )
A．xB．2xC．x＋4D．x(x＋4)
5．计算的结果是( )
A．B．C．yD．x
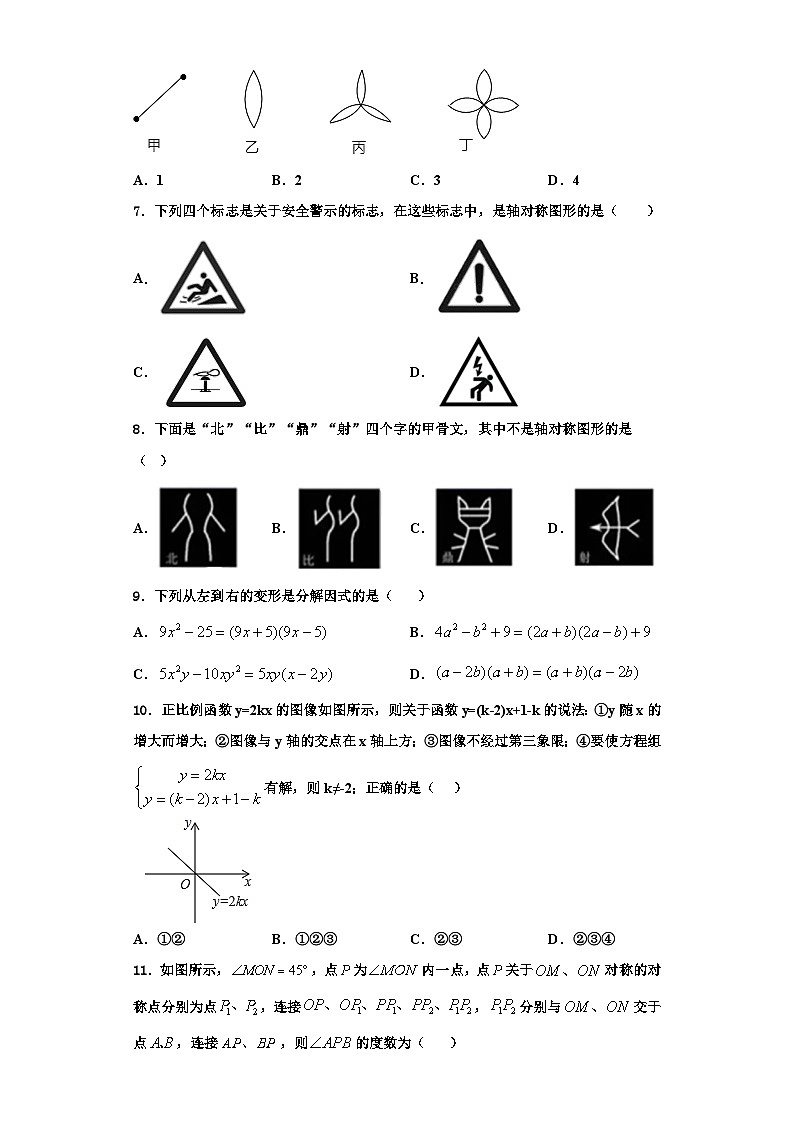
6．下列四个图形中，是轴对称图形的个数是（ ）
A．1B．2C．3D．4
7．下列四个标志是关于安全警示的标志，在这些标志中，是轴对称图形的是（ ）
A．B．
C．D．
8．下面是“北”“比”“鼎”“射”四个字的甲骨文，其中不是轴对称图形的是（ ）
A．B．C．D．
9．下列从左到右的变形是分解因式的是（ ）
A．B．
C．D．
10．正比例函数y=2kx的图像如图所示，则关于函数y=(k-2)x+1-k的说法：①y随x的增大而增大；②图像与y轴的交点在x轴上方；③图像不经过第三象限；④要使方程组有解，则k≠-2；正确的是（ ）

A．①②B．①②③C．②③D．②③④
11．如图所示，，点为内一点，点关于对称的对称点分别为点，连接，分别与交于点，连接，则的度数为（ ）
A．B．C．D．
12．如图，，，，是数轴上的四个点，其中最适合表示无理数的点是（ ）
A．点B．.点C．点D．点
二、填空题（每题4分，共24分）
13．我们规定：等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”，记作k．若，则该等腰三角形的顶角为______________度．
14．已知点P(a，b)在一次函数y＝2x﹣1的图象上，则4a﹣2b+1＝_____．
15．长、宽分别为、的长方形，它的周长为16，面积为10，则的值为____.
16．一个三角形的两边的长分别是3和5，要使这个三角形为直角三角形，则第三条边的长为_____．
17．分解因式：________．
18．如图所示，在中，，将点C沿折叠，使点C落在边D点，若，则______．
三、解答题（共78分）
19．（8分）2019年10月，某市高质量通过全国文明城市测评，该成绩的取得得益于领导高度重视（A）、整改措施有效（B）、市民积极参与（C）、市民文明素质（D）．某数学兴趣小组随机走访了部分市民，对这四项认可度进行调查（只选填最认可的一项），并将调查结果制作了如下两幅不完整的统计图．
（1）请补全D项的条形图；
（2）已知B、C两项条形图的高度之比为3：1．
①选B、C两项的人数各为多少个？
②求α的度数，

20．（8分）如图，在平面直角坐标系中，，，
（1）画出关于轴的对称图形，并写出点、的坐标
（2）直接写出的面积
（3）在轴负半轴上求一点，使得的面积等于的面积
21．（8分）化简分式：,并从1,2,3,4这四个数中取一个合适的数作为x的值代入求值．
22．（10分）如图，在平面直角坐标系中，点为正半轴上一点，过点的直线轴，且直线分别与反比例函数和的图像交于两点，.
求的值；
当时，求直线的解析式；
在的条件下，若轴上有一点，使得为等腰三角形，请直接写出所有满足条件的点的坐标.
23．（10分）某学校初二年级在元旦汇演中需要外出租用同一种服装若干件，已知在没有任何优惠的情况下，同时在甲服装店租用2件和乙服装店租用3件共需280元，在甲服装店租用4件和乙服装店租用一件共需260元．
（1）求两个服装店提供的单价分别是多少？
（2）若该种服装提前一周订货则甲乙两个租售店都可以给予优惠，具体办法如下：甲服装店按原价的八折进行优惠；在乙服装店如果租用5件以上，则超出5件的部分可按原价的六折进行优惠；设需要租用（）件服装，选择甲店则需要元，选择乙店则需要元，请分别求出，关于的函数关系式；
（3）若租用的服装在5件以上，请问租用多少件时甲乙两店的租金相同？
24．（10分）如图，在等边中，点（2，0），点是原点，点是轴正半轴上的动点，以为边向左侧作等边，当时，求的长．
25．（12分）如图是学习“分式方程应用”时,老师板书的例题和两名同学所列的方程．
15.3分式方程
例:有甲、乙两个工程队，甲队修路米与乙队修路米所用时间相等．乙队每天比甲队多修米,求甲队每天修路的长度．
冰冰:
庆庆:
根据以上信息,解答下列问题:
（1）冰冰同学所列方程中的表示_____,庆庆同学所列方 程中的表示；
（2）两个方程中任选一个,写出它的等量关系；
（3）解（2）中你所选择的方程,并解答老师的例题．
26．如图，三个顶点的坐标分别为，，．
（1）画出关于轴对称的图形，并写出三个顶点的坐标；
（2）在轴上作出一点，使的值最小，求出该最小值.（保留作图痕迹）
参考答案
一、选择题（每题4分，共48分）
1、A
【分析】直接利用多边形内角和定理即可求解．
【详解】解：设这个多边形的边数为n，
则（n－2）×180°＝n
解得：n＝7
故选：A
【点睛】
本题主要考查多边形内角和定理，关键要掌握多边形内角和定理：n边形的内角和是（n－2）×180°（n≥3，且n为整数）．
2、D
【详解】试题分析：∵ D为BC中点，∴CD=BD，又∵∠BDO=∠CDO=90°，∴在△ABD和△ACD中，
，∴△ABD≌△ACD；∵EF垂直平分AC，∴OA=OC，AE=CE，在△AOE和△COE中，
，∴△AOE≌△COE；在△BOD和△COD中，，∴△BOD≌△COD；
在△AOC和△AOB中，，∴△AOC≌△AOB；所以共有4对全等三角形，故选D．
考点：全等三角形的判定.
3、B
【分析】根据题意可以列出相应的二元一次方程组，从而本题得以解决．
【详解】用一根绳子去量一根长木，绳子还剩余4.5尺,
则，
将绳子对折再量长木，长木还剩余1尺，
则，
∴，
故选B.
【点睛】
本题考查由实际问题抽象出二元一次方程组，解题的关键是明确题意，列出相应的二元一次方程组．
4、D
【分析】根据各分母寻找公分母x(x＋4)，方程两边乘最简公分母，可以把分式方程转化为整式方程．
【详解】解：方程两边同乘x(x＋4)，得2x=1
故选D．
5、A
【详解】原式 ，故选A.
6、D
【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形进行分析即可．
【详解】解：根据题意，甲、乙、丙、丁都是轴对称图形，共4个，
故选：D．
【点睛】
本题考查了轴对称图形的特征，掌握轴对称图形的特征是解题的关键．
7、B
【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴可得答案．
【详解】解：A、不是轴对称图形，故此选项错误；
B、是轴对称图形，故此选项正确；
C、不是轴对称图形，故此选项错误；
D、不是轴对称图形，故此选项错误；
故选：B．
【点睛】
此题主要考查了轴对称图形，关键是掌握轴对称图形的概念．
8、B
【解析】根据轴对称的定义，逐一判断选项，即可得到答案．
【详解】A是轴对称图形，不符合题意，
B不是轴对称图形，符合题意，
C是轴对称图形，不符合题意，
D是轴对称图形，不符合题意，
故选B．
【点睛】
本题主要考查轴对称图形的定义，掌握轴对称图形的定义，是解题的关键．
9、C
【分析】考查因式分解的概念：把一个多项式分解成几个整式的积的形式.
【详解】解：A. 正确分解为：，所以错误；
B．因式分解后为积的形式，所以错误；
C．正确；
D.等式左边就不是多项式，所以错误.
【点睛】
多项式分解后一定是几个整式相乘的形式，才能叫因式分解
10、D
【分析】根据正比例函数y=2kx过二，四象限，判断出k的取值范围，然后可得k-2和1-k的取值范围，即可判断①②③，解方程组，根据分式有意义的条件即可判断④．
【详解】解：由图像可得正比例函数y=2kx过二，四象限，
∴2k