重庆市南川区部分学校2023年数学八年级第一学期期末达标检测试题【含解析】

这是一份重庆市南川区部分学校2023年数学八年级第一学期期末达标检测试题【含解析】，共21页。试卷主要包含了下列各组线段，能构成三角形的是，若分式有意义，则取值范围是，若点A在y轴上，则点B位于等内容，欢迎下载使用。
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题（每题4分，共48分）
1．要使分式有意义，x的取值应满足（ ）
A．x≠1B．x≠﹣2C．x≠1或x≠﹣2D．x≠1且x≠﹣2
2．下列逆命题是真命题的是（ ）
A．如果x=y，那么x2=y2
B．相等的角是内错角
C．有三个角是60°的三角形是等边三角形
D．全等三角形的对应角相等
3．如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是
A．∠A=∠CB．AD=CBC．BE=DFD．AD∥BC
4．下列各组线段，能构成三角形的是( )
A．B．
C．D．
5．若分式有意义，则取值范围是（ ）
A．B．C．D．
6．若点A(n，2)在y轴上，则点B(2n－1，3n+1)位于（ ）
A．第四象限．B．第三象限C．第二象限D．第一象限
7．若代数式有意义，则实数x的取值范围是（ ）
A．x=0B．x=3C．x≠0D．x≠3
8．一个正方形的面积等于30，则它的边长a满足（ ）
A．4＜a＜5B．5＜a＜6C．6＜a＜7D．7＜a＜8
9．若是下列某二元一次方程组的解，则这个方程组为（ ）
A．B．
C．D．
10．如图，在直角△ABC中，，AB=AC，点D为BC中点，直角绕点D旋转，DM，DN分别与边AB，AC交于E，F两点，下列结论：①△DEF是等腰直角三角形；② AE=CF；③△BDE≌△ADF；④ BE+CF=EF，其中正确结论是（ ）
A．①②④B．②③④C．①②③D．①②③④
11．如图，在中，，分别以顶点，为圆心，大于长为半径作弧，两弧交于点，，作直线交于点.若，，则长是（ ）
A．7B．8C．12D．13
12．如图所示，△ABC中AC边上的高线是（ ）
A．线段DAB．线段BAC．线段BDD．线段BC
二、填空题（每题4分，共24分）
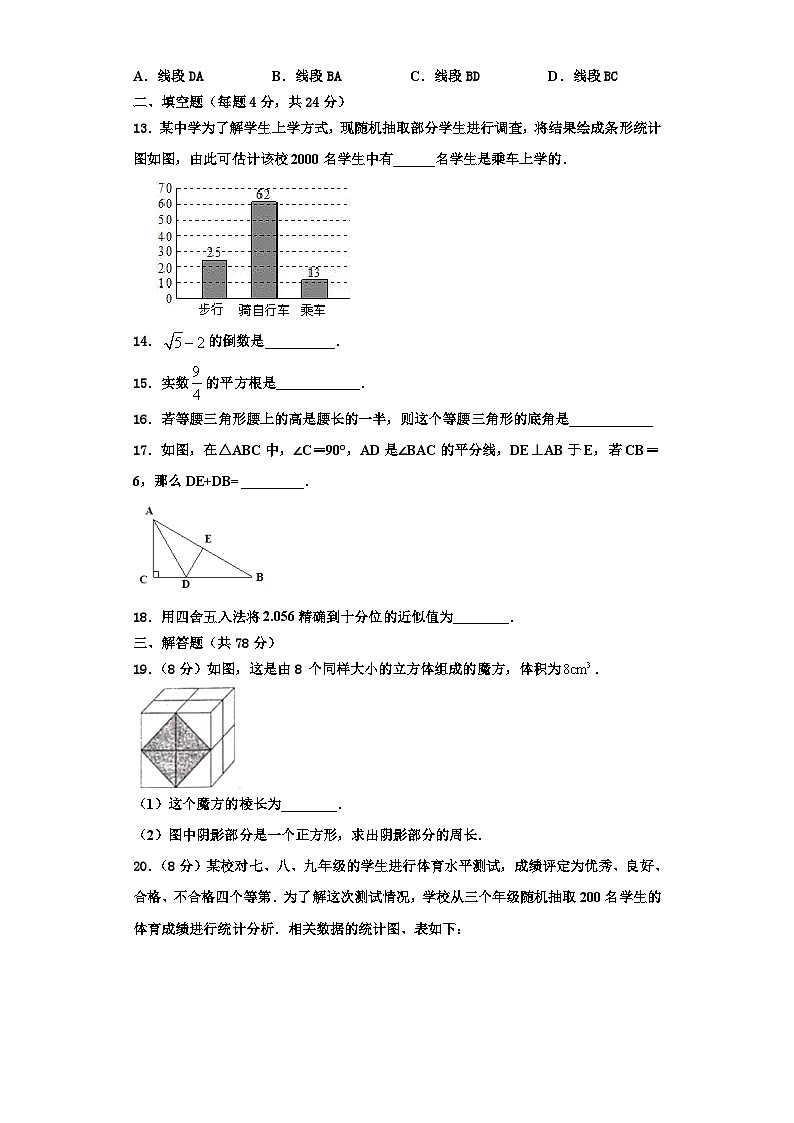
13．某中学为了解学生上学方式，现随机抽取部分学生进行调查，将结果绘成条形统计图如图，由此可估计该校2000名学生中有______名学生是乘车上学的．
14．的倒数是__________．
15．实数的平方根是____________．
16．若等腰三角形腰上的高是腰长的一半，则这个等腰三角形的底角是____________
17．如图，在△ABC中，∠C＝90°，AD是∠BAC的平分线，DE⊥AB于E，若CB＝6，那么DE+DB=_________．
18．用四舍五入法将2.056精确到十分位的近似值为________．
三、解答题（共78分）
19．（8分）如图，这是由8 个同样大小的立方体组成的魔方，体积为．
（1）这个魔方的棱长为________．
（2）图中阴影部分是一个正方形，求出阴影部分的周长．
20．（8分）某校对七、八、九年级的学生进行体育水平测试，成绩评定为优秀、良好、合格、不合格四个等第．为了解这次测试情况，学校从三个年级随机抽取200名学生的体育成绩进行统计分析．相关数据的统计图、表如下：
根据以上信息解决下列问题：
（1）在统计表中，a的值为 ，b的值为 ；
（2）在扇形统计图中，八年级所对应的扇形圆心角为 度；
（3）若该校三个年级共有2000名学生参加考试，试估计该校学生体育成绩不合格的人数．
21．（8分）已知：如图①，是等边三角形，是边上一点，平行交于点．
（1）求证：是等边三角形
（2）连接，延长至点，使得，如图②．求证：．
22．（10分）已知：如图，点在同一条直线上，求证：
23．（10分）解下列分式方程：
（1）＝1
（2）
24．（10分）观察下列两个数的积(这两个数的十位上的数相同，个位上的数的和等于)，你发现结果有什么规律?
；
；
；
；
（1）设这两个数的十位数字为，个位数字分别为和，请用含和的等式表示你发现的规律；
（2）请验证你所发现的规律；
（3）利用你发现的规律直接写出下列算式的答案．
； ； ； ．
25．（12分）已知：在平面直角坐标系中，点为坐标原点，的顶点的坐标为，顶点在轴上(点在点的右侧)，点在上，连接，且．
(1)如图1，求点的纵坐标；
(2)如图2，点在轴上(点在点的左侧)，点在上，连接交于点；若，求证：
(3)如图3，在(2)的条件下，是的角平分线，点与点关于轴对称，过点作分别交于点，若，求点的坐标．
26．已知：△ABC中，BO平分∠ABC，CO平分∠ACB
（1）如图1，∠BOC和∠A有怎样的数量关系？请说明理由
（2）如图2，过O点的直线分别交△ABC的边AB、AC于E、F（点E不与A，B重合，点F不与A、C重合），BP平分外角∠DBC，CP平分外角∠GCB，BP，CP相交于P．求证：∠P＝∠BOE+∠COF；
（3）如果（2）中过O点的直线与AB交于E（点E不与A、B重合），与CA的延长线交于F在其它条件不变的情况下，请直接写出∠P、∠BOE、∠COF三个角之间的数量关系．
参考答案
一、选择题（每题4分，共48分）
1、D
【分析】根据分式的分母不为0来列出不等式，解不等式即可得到答案．
【详解】解：由题意得，（x+2）（x﹣1）≠0，
解得，x≠1且x≠﹣2，
故选：D．
【点睛】
本题考查的是分式有意义的条件，掌握分式的分母不为0是解题的关键．
2、C
【分析】先写出各选项的逆命题，然后逐一判断即可得出结论．
【详解】A． 如果x=y，那么x2=y2的逆命题为：如果x2=y2，那么x=y,是假命题，故A选项不符合题意；
B． 相等的角是内错角的逆命题为：内错角相等,是假命题，故B选项不符合题意；
C． 有三个角是60°的三角形是等边三角形的逆命题为：等边三角形的三个角都是60°，是真命题，故C选项符合题意；
D． 全等三角形的对应角相等的逆命题为：对应角相等的两个三角形全等,是假命题，故D选项不符合题意；
故选C．
【点睛】
此题考查的是写一个命题的逆命题和判断逆命题的真假，掌握平方的意义、等边三角形的性质和全等三角形的判定是解决此题的关键．
3、B
【解析】试题分析：∵AE=CF，∴AE+EF=CF+EF．∴AF=CE．
A．∵在△ADF和△CBE中，，∴△ADF≌△CBE（ASA），正确，故本选项错误．
B．根据AD=CB，AF=CE，∠AFD=∠CEB不能推出△ADF≌△CBE，错误，故本选项正确．
C．∵在△ADF和△CBE中，，∴△ADF≌△CBE（SAS），正确，故本选项错误．
D．∵AD∥BC，∴∠A=∠C．由A选项可知，△ADF≌△CBE（ASA），正确，故本选项错误．
故选B．
4、C
【分析】判断三条线段能否构成三角形，只需让两个较短的线段长度相加，其和若大于最长线段长度，则可以构成三角形，否则不能构成三角形.逐一判断即可.
【详解】A选项，1+34，可以构成三角形；
D选项，8+8