重庆市沙坪坝区南开中学2023年数学八上期末教学质量检测试题【含解析】

这是一份重庆市沙坪坝区南开中学2023年数学八上期末教学质量检测试题【含解析】，共23页。试卷主要包含了分式方程 的解是，下列图形是轴对称图形的是等内容，欢迎下载使用。
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．若是完全平方式，则m的值等于（ ）
A．1或5B．5C．7D．7或
2．如图，四边形ABCD中，AB＝AD，点B关于AC的对称点B′ 恰好落在CD上，若∠BAD＝110°，则∠ACB的度数为( )
A．40°B．35°C．60°D．70°
3．在下列说法中：
①有一个外角是 120°的等腰三角形是等边三角形．
② 有两个外角相等的等腰三角形是等边三角形．
③ 有一边上的高也是这边上的中线的等腰三角形是等边三角形．
④ 三个外角都相等的三角形是等边三角形．
其中正确的有（ ）
A．1 个B．2 个C．3 个D．4 个
4．已知等腰三角形的周长是22，其中一边长为8，则其它两边的长度分别是（ ）
A．3和11B．7和7C．6和8或7和7D．3和11或7和7
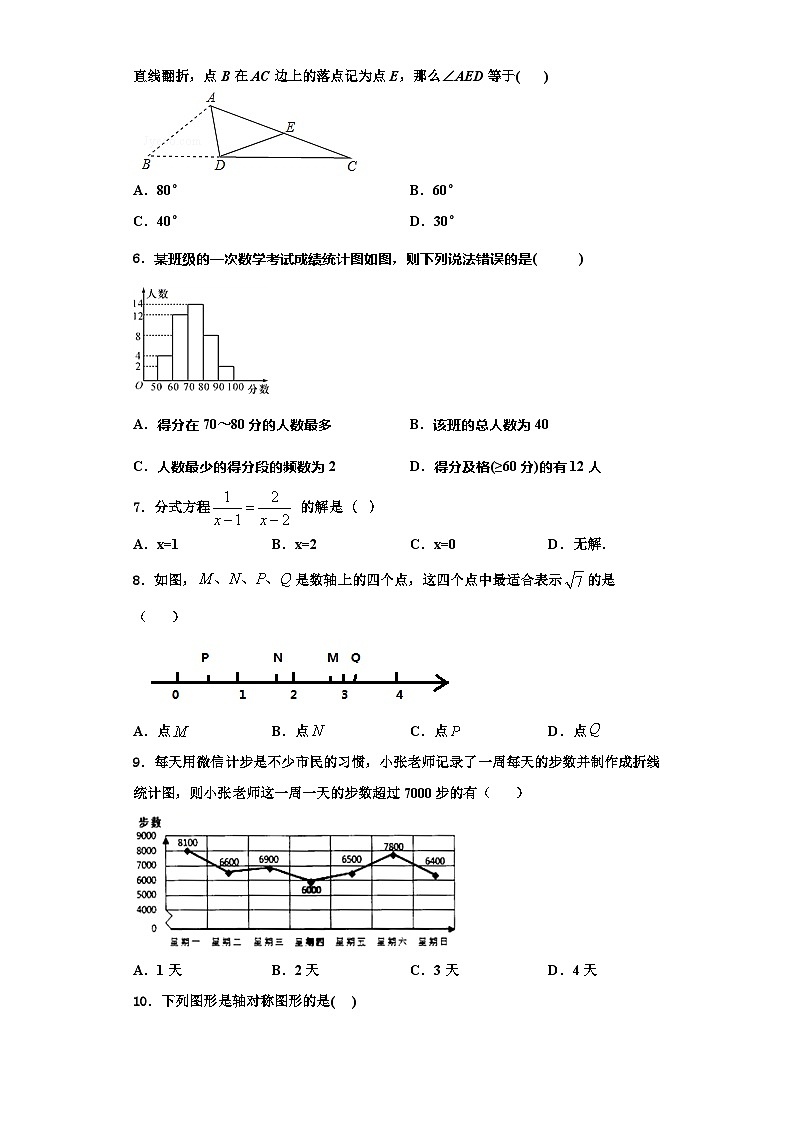
5．如图，AD是△ABC的角平分线，∠C=20°，AB+BD=AC，将△ABD沿AD所在直线翻折，点B在AC边上的落点记为点E，那么∠AED等于( )
A．80°B．60°
C．40°D．30°
6．某班级的一次数学考试成绩统计图如图，则下列说法错误的是( )
A．得分在70～80分的人数最多B．该班的总人数为40
C．人数最少的得分段的频数为2D．得分及格(≥60分)的有12人
7．分式方程 的解是（ ）
A．x=1B．x=2C．x=0D．无解．
8．如图，是数轴上的四个点，这四个点中最适合表示的是 （ ）
A．点B．点C．点D．点
9．每天用微信计步是不少市民的习惯，小张老师记录了一周每天的步数并制作成折线统计图，则小张老师这一周一天的步数超过7000步的有（ ）
A．1天B．2天C．3天D．4天
10．下列图形是轴对称图形的是( )
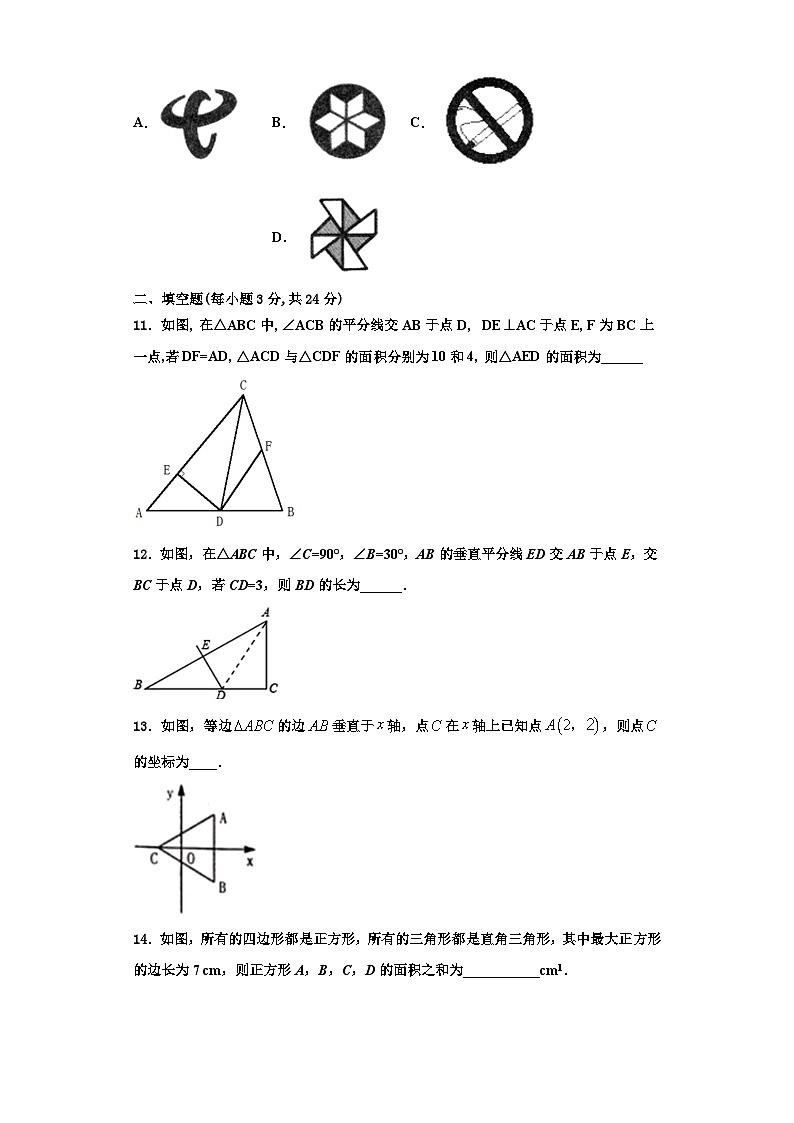
A．B．C．D．
二、填空题(每小题3分,共24分)
11．如图, 在△ABC中, ∠ACB的平分线交AB于点D, DE⊥AC于点E, F为BC上一点,若DF=AD, △ACD与△CDF的面积分别为10和4, 则△AED的面积为______
12．如图，在△ABC中，∠C=90°，∠B=30°，AB的垂直平分线ED交AB于点E，交BC于点D，若CD=3，则BD的长为______．
13．如图，等边的边垂直于轴，点在轴上已知点，则点的坐标为____．
14．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为7 cm，则正方形A，B，C，D的面积之和为___________cm1．
15．华为手机上使用的芯片, ,则用科学记数法表示为__________
16．在平面直角坐标系xOy中，已知点A（0，1），B（1，2），点P在x轴上运动，当点P到A、B两点距离之差的绝对值最大时，点P的坐标是_______．
17．已知am=3，an=2，则a2m﹣n的值为_____．
18．如图，中，，，垂足为，，，点从点出发沿线段的方向移动到点停止，连接.若与的面积相等，则线段的长度是______．
三、解答题(共66分)
19．（10分）如图，平分，平分外角，．
（1）求证：；
（2）若，求的度数．
20．（6分）阅读下面内容，并解答问题．
（1）请补充要求证的结论，并写出证明过程；
（2）请从下列A、B两题中任选一题作答，我选择_______题．
A．在图1的基础上，分别作的平分线与的平分线交于点，得到图2，则的度数为_______．
B．如图3，，直线分别交，于点，．点在直线，之间，且在直线右侧，的平分线与的平分线交于点，则与满足的数量关系为_______．
21．（6分）已知x1+y1+6x﹣4y+13=0，求（xy）﹣1．
22．（8分）如图，在△ABC中，D为BC的中点，过D点的直线GF交AC于点F，交AC的平行线BG于点G，DE⊥GF，并交AB于点E，连接EG，EF．
（1）求证：BG＝CF．
（2）请你猜想BE＋CF与EF的大小关系，并说明理由．
23．（8分）如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E．
（1）依题意补全图形；
（2）若∠PAC＝20°，求∠AEB的度数；
24．（8分）如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B在x轴的正半轴上．∠OAB=90°且OA=AB，OB=6，OC=1．点P是线段OB上的一个动点(点P不与点O，B重合)，过点P的直线与y轴平行，直线交边OA或边AB于点Q，交边OC或边BC于点R．设点P的横坐标为t，线段QR的长度为m．已知t=4时，直线恰好过点C.
（1）求点A和点B的坐标；
（2）当0＜t＜3时，求m关于t的函数关系式；
（3）当m=3.1时，请直接写出点P的坐标.
25．（10分）如图（1），方格图中每个小正方形的边长为1，点A、B、C都是格点．
（1）画出关于直线MN对称的；
（2）写出的长度；
（3）如图（2），A，C是直线MN同侧固定的点，是直线MN上的一个动点，在直线MN上画出点，使最小．
26．（10分）对于任意一个三位数，将它任意两个数位上的数字对调后得到一个首位不为0的新的三位数（可以与相同），记，在所有可能的情况中，当最小时，我们称此时的是的“平安快乐数”，并规定.例如：318按上述方法可得新数381、813、138，因为，，，而，所以138是318的“平安快乐数”，此时.
（1）168的“平安快乐数”为_______________，______________；
（2）若（，都是正整数），交换其十位与百位上的数字得到新数，当是13的倍数时，求的最大值.
参考答案
一、选择题(每小题3分,共30分)
1、D
【分析】根据完全平方公式，首末两项是x和4这两个数的平方，那么中间一项为加上或减去x和4积的2倍．
【详解】解：∵多项式是完全平方式，
∴，
∴
解得：m=7或-1
故选：D.
【点睛】
此题主要查了完全平方公式的应用；两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．
2、B
【分析】连接AB'，BB'，过A作AE⊥CD于E，依据∠BAC=∠B'AC，∠DAE=∠B'AE，即可得出∠CAE= ∠BAD，再根据四边形内角和以及三角形外角性质，即可得到∠ACB=∠ACB'=90°-∠BAD．
【详解】
解：如图，连接AB'，BB'，过A作AE⊥CD于E，
∵点B关于AC的对称点B'恰好落在CD上，
∴AC垂直平分BB'，
∴AB=AB'，
∴∠BAC=∠B'AC，
∵AB=AD，
∴AD=AB'，
又∵AE⊥CD，
∴∠DAE=∠B'AE，
∴∠CAE=∠BAD=55°，
又∵∠AEC=90°，
∴∠ACB=∠ACB'=35°，
故选B．
【点睛】
本题主要考查了轴对称的性质，四边形内角和以及三角形外角性质的运用，解决问题的关键是作辅助线构造四边形AOB'E，解题时注意：如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．
3、B
【分析】根据有一个角等于60°的等腰三角形是等边三角形，三个角相等的三角形是等边三角形进行分析即可．
【详解】解：①有一个外角是120°的等腰三角形是等边三角形，说法正确；
②有两个外角相等的等腰三角形是等边三角形，说法错误；
③有一边上的高也是这边上的中线的三角形是等边三角形，说法错误；
④三个外角都相等的三角形是等边三角形，说法正确，
正确的命题有2个，
故选：B．
【点睛】
此题主要考查了命题与定理，关键是掌握等边三角形的判定方法．
4、C
【分析】要确定等腰三角形的另外两条边长,可以根据已知的边长,结合周长公式求解,由于长为8的边没有明确是腰还是底边,要进行分类讨论.
【详解】解:等腰三角形的周长是22.
当8为腰时,它的底边长,,能构成等腰三角形.
当8为底时,它的腰长,,能构成等腰三角形.
即它两边的长度分别是6和8或7和7.
故选:C.
【点睛】
本题考查了等腰三角形的性质和三角形的三边关系,注意检验三角形三边长是否构成三角形.
5、C
【解析】根据折叠的性质可得BD＝DE，AB＝AE，然后根据AC＝AE+EC，AB+BD＝AC，证得DE＝EC，根据等边对等角以及三角形的外角的性质求解．
【详解】根据折叠的性质可得：BD＝DE，AB＝AE．
∵AC＝AE+EC，AB+BD＝AC，∴DE＝EC，∴∠EDC＝∠C＝20°，∴∠AED＝∠EDC+∠C＝40°．
故选C．
【点睛】
本题考查了折叠的性质以及等腰三角形的性质、三角形的外角的性质，证明DE＝EC是解答本题的关键．
6、D
【解析】试题分析：A、得分在70～80分之间的人数最多，有14人，此选项正确；
B、该班的总人数为4＋12＋14＋8＋2＝40人，此选项正确；
C、得分在90～100分之间的人数最少，有2人，频数为2，此选项正确；
D、及格（≥60分）人数是12＋14＋8＋2＝36人，此选项错误．
故选D．
点睛：本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
7、C
【解析】分析：首先进行去分母将分式方程转化为整式方程，然后解一元一次方程，最后对方程的根进行检验．
详解：去分母可得：x－2=2(x－1)， 解得：x=0，
经检验：x=0是原方程的解， ∴分式方程的解为x=0， 故选C．
点睛：本题主要考查的是解分式方程的方法，属于基础题型．去分母是解分式方程的关键所在，还要注意分式方程最后必须进行验根．
8、A
【分析】根据 进行判断即可．
【详解】∵
∴
∴点最适合表示
故答案为：A．
【点睛】
本题考查了用数轴上的点表示无理数的问题，掌握要表示的数的大小范围是解题的关键．
9、B
【分析】根据折线统计图进行统计即可.
【详解】根据统计图可得：小张老师这一周一天的步数超过7000步的有：星期一，星期六，共2天.
故选：B
【点睛】
本题考查的是折线统计图，能从统计图中正确的读出信息是关键.
10、B
【解析】根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．据此对图中的图形进行判断．
解：A、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，故本选项错误；
B、有六条对称轴，是轴对称图形，故本选项正确；
C、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，故本选项错误；
D、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，故本选项错误．
故选B．
二、填空题(每小题3分,共24分)
11、1
【分析】如图（见解析），过点D作，根据角平分线的性质可得，再利用三角形全等的判定定理得出，从而有，最后根据三角形面积的和差即可得出答案．
【详解】如图，过点D作
平分，
又
则
解得
故答案为：1．
【点睛】
本题考查了角平分线的性质、直角三角形全等的判定定理等知识点，通过作辅助线，构造两个全等的三角形是解题关键．
12、1
【分析】根据线段垂直平分线的性质求出AD=BD，求出∠BAD=∠B=30°，求出∠CAD=30°，根据含30°角的直角三角形的性质求出AD即可．
【详解】∵DE是线段AB的垂直平分线，
∴AD=BD，
∵∠B=30°，
∴∠BAD=∠B=30°，
又∵∠C=90°
∴∠CAB=90°-∠B=90°-30°=10°，
∴∠DAC=∠CAB-∠BAD=10°-30°=30°，
∴在Rt△ACD中，AD=2CD=1，
∴BD=AD=1．
故答案为：1．
【点睛】
本题考查的是线段垂直平分线的性质，含30°角的直角三角形的性质，掌握线段垂直平分线上任意一点，到线段两端点的距离相等是解题的关键．
13、
【分析】根据等边三角形的性质以及30°的直角三角形的性质求出AC的长度，再利用勾股定理求出CE的长度即可得出答案．
【详解】如图：
设AB与x轴交于E点
∵AB⊥CE
∴∠CEA=90°
∵
∴AE=2,OE=2
∵△ABC是等边三角形，CE⊥AB
∴
在Rt△ACE中，AC=2AE=4
∴
∴
∴点C的坐标为
故答案为：
【点睛】
本题考查了等边三角形,30°的直角三角形的性质，勾股定理，掌握等边三角形,30°的直角三角形的性质，勾股定理是解题的关键．
14、2
【分析】根据正方形的面积公式，连续运用勾股定理，发现：四个小正方形的面积和等于最大正方形的面积．
【详解】解：如图，
∵所有的三角形都是直角三角形，所有的四边形都是正方形，
∴正方形A的面积=a1，正方形B的面积=b1，
正方形C的面积=c1，正方形D的面积=d1，
又∵a1+b1=x1，c1+d1=y1，
∴正方形A、B、C、D的面积和=(a1+b1)+(c1+d1)=x1+y1=71=2cm1．
故答案为：2．
【点睛】
本题考查了勾股定理，注意掌握直角三角形中，两直角边的平方和等于斜边的平方是解答本题的关键．
15、
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【详解】解：．
故答案为：．
【点睛】
本题考查用科学记数法表示较小的数，一般形式为，其中，为由原数左边起第一个不为零的数字前面的0的个数所决定．
16、（﹣1，0）
【详解】解：由三角形两边之差小于第三边可知，
当A、B、P三点不共线时，由三角形三边关系|PA﹣PB|＜AB；
当A、B、P三点共线时，∵A（0，1），B（1，2）两点都在x轴同侧，∴|PA﹣PB|=AB．
∴|PA﹣PB|≤AB．
∴本题中当点P到A、B两点距离之差的绝对值最大时，点P在直线AB上．
设直线AB的解析式为y=kx+b，
∵A（0，1），B（1，2），∴，解得．
∴直线AB的解析式为y=x+1．
令y=0，得0=x+1，解得x=﹣1．
∴点P的坐标是（﹣1，0）．
故答案为：（﹣1，0）．
17、4.1
【解析】分析：首先根据幂的乘方的运算方法，求出a2m的值；然后根据同底数幂的除法的运算方法，求出a2m-n的值为多少即可．
详解：∵am=3，
∴a2m=32=9，
∴a2m-n==4.1．
故答案为4.1．
点睛：此题主要考查了同底数幂的除法法则，以及幂的乘方与积的乘方，同底数幂相除，底数不变，指数相减，要熟练掌握，解答此题的关键是要明确：①底数a≠0，因为0不能做除数；②单独的一个字母，其指数是1，而不是0；③应用同底数幂除法的法则时，底数a可是单项式，也可以是多项式，但必须明确底数是什么，指数是什么．
18、2
【分析】当△ADE与△CDE的面积相等时，DE∥AC，此时△BDE∽△BCA，利用相似三角形的对应边成比例进行解答即可．
【详解】解：如下图示，依题意得，当DE∥AC时，△ADE与△CDE的面积相等，
此时△BDE∽△BCA，
所以 BE:AB=BD:BC,
因为AB=CB, 所以BE=BD
所以．
【点睛】
本题考查了相似三角形的判定与性质，平行线间的距离以及三角形的面积．根据题意得到当DE∥AC时，△ADE与△CDE的面积相等是解题的难点．
三、解答题(共66分)
19、（1）详见解析；（2）．
【分析】（1）由已知条件可得，根据同位角相等，两直线平行即可得；
（2）根据角平分线的定义，可得出，，再根据外角的性质可得与，通过角度的计算可得出答案．
【详解】（1）证明：∵平分外角，
∴，
又∵，
∴，
∴．
（2）解：∵BE、CE分别是△ABC内角∠ABC和外角∠ACD的平分线，
∴，，
又∵∠ACD是△ABC的外角，
∴，
∴
∵∠ECD是△BCE的外角，
∴
∴，
∵∠A=50°，
∴．
【点睛】
本题考查了角平分线的定义和三角形外角的性质，熟练运用三角形外角的性质进行角度的计算是解题的关键．
20、（1）；证明见解析；（2）A．，B．．
【分析】（1）由AB∥CD，可知∠BEF与∠DFE互补，由角平分线的性质可得，由三角形内角和定理可得∠G＝，则；
（2）A，由（1）可知,根据角平分线的性质可得,故,根据三角形的内角和即可求出=；
B，设，，故=，再得到,根据角平分线的性质可得,则,再求出，即可比较得到结论．
【详解】（1）；
证明：，
，
平分，平分，
，，
．
在中，，
，
．
（2）A，由（1）可知,
∵的平分线与的平分线交于点
∴,
则,
∴==
故答案为：A;45；
B，设，，
∴=，
则,
∵的平分线与的平分线交于点
∴,
∴,
∴==，
∵=，
故
故答案为：B;．
【点睛】
本题考查了平行线的性质、角平分线的定义、三角形内角和定理，熟练掌握这些定理是解题的关键．
21、
【分析】已知等式变形后，利用非负数的性质求出x与y的值，即可确定出所求式子的值．
【详解】解：∵x1+y1+6x﹣4y+13=0，
∴（x+3）1+（y﹣1）1=0，
∴x+3=0，y﹣1=0，
∴x=﹣3，y=1，
∴（xy）﹣1=（﹣3×1）﹣1=．
考点：配方法的应用；非负数的性质：偶次方．
22、（1）见解析；（2）BE+CF＞EF，理由见解析
【分析】（1）求出∠C=∠GBD，BD=DC，根据ASA证出△CFD≌△BGD即可．
（2）根据全等得出BG=CF，根据三角形三边关系定理求出即可．
【详解】解：（1）证明：∵BG∥AC，
∴∠C=∠GBD，
∵D是BC的中点，
∴BD=DC，
在△CFD和△BGD中
，
∴△CFD≌△BGD，
∴BG=CF．
（2）BE+CF＞EF，
理由如下：
∵△CFD≌△BGD，
∴CF=BG，
在△BGE中，BG+BE＞EG，
∵△CFD≌△BGD，
∴GD=DF，ED⊥GF，
∴EF=EG，
∴BE+CF＞EF．
【点睛】
本题考查了全等三角形的性质和判定，平行线的性质，线段垂直平分线性质，三角形三边关系定理的应用，主要考查学生的推理能力．
23、（1）见详解；（2）60°
【分析】（1）作出点C关于直线AP的对称点为点D，连接AD，BD，即可得到所作图形；
（2）由等边三角形的性质和轴对称的性质，可得AB=AD，∠BAD=100°，结合三角形内角和定理，求出∠ADB的度数，然后由三角形外角的性质，即可求解．
【详解】（1）补全图形，如图所示：
（2）∵点C关于直线AP的对称点为点D，
∴AC=AD，∠PAD=∠PAC＝20°，
∵三角形ABC是等边三角形，
∴AB=AC，∠BAC=60°，
∴AB=AD，∠BAD=60°+20°+20°=100°，
∴∠ADB=（180°-100°）÷2=40°，
∴∠AEB=∠ADB+∠PAD=40°+20°=60°．
【点睛】
本题主要考查等边三角形的性质，等腰三角形的性质，轴对称的性质，三角形内角和定理以及三角形外角的性质，熟练掌握上述性质定理，是解题的关键．
24、（1）（3，3），（6，0） （2）（0