重庆市实验学校2023-2024学年数学八年级第一学期期末教学质量检测试题【含解析】

这是一份重庆市实验学校2023-2024学年数学八年级第一学期期末教学质量检测试题【含解析】，共18页。试卷主要包含了考生必须保证答题卡的整洁，若六边形的最大内角为度，则必有，已知，则=等内容，欢迎下载使用。
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．已知：一次函数的图像经过点A（，1）和点B（，-3）且＜，则它的图像大致是（ ）．
A．B．C．D．
2．如图，在等边中，，将线段沿翻折，得到线段，连结交于点，连结、以下说法：①，②，③，④中，正确的有（ ）
A．个B．个C．个D．个
3．甲乙两地相距420千米,新修的高速公路开通后,在甲、乙两地行驶的长途客运车平均速度是原来的1.5倍,进而从甲地到乙地的时间缩短了2小时．设原来的平均速度为x千米/时,可列方程为（ ）
A．B．
C．D．
4．若六边形的最大内角为度，则必有（ ）
A．B．C．D．
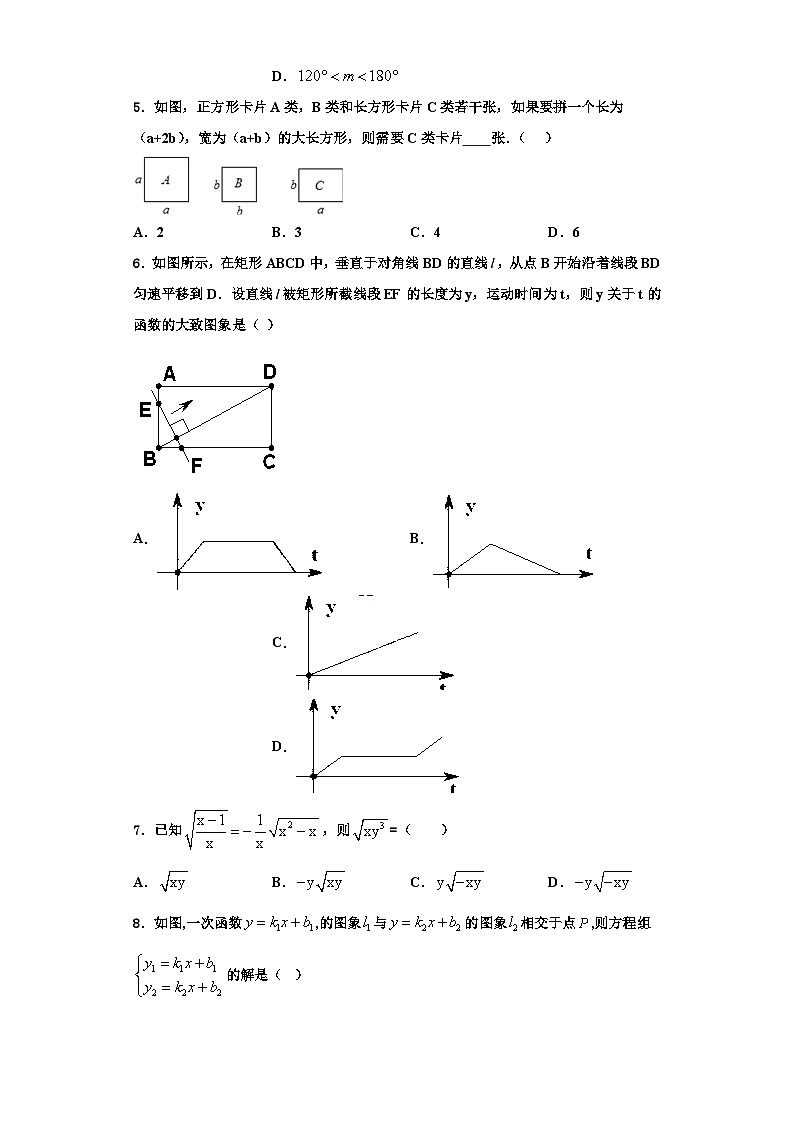
5．如图，正方形卡片A类，B类和长方形卡片C类若干张，如果要拼一个长为（a+2b），宽为（a+b）的大长方形，则需要C类卡片 张．（ ）
A．2B．3C．4D．6
6．如图所示，在矩形ABCD中，垂直于对角线BD的直线，从点B开始沿着线段BD匀速平移到D．设直线被矩形所截线段EF的长度为y，运动时间为t，则y关于t的函数的大致图象是（ ）
A．B．C．D．
7．已知，则=（ ）
A．B．C．D．
8．如图,一次函数,的图象与的图象相交于点,则方程组的解是（ ）
A．B．C．D．
9．下列长度的三条线段可以组成三角形的是（ ）
A．3，4，8B．5，6，11C．1，2，3D．5，6，10
10．长度单位1纳米=10-9米，目前发现一种新型禽流感病毒（H7N9）的直径约为101纳米，用科学记数法表示该病毒直径是( )
A．10.l×l0-8米B．1.01×l0-7米C．1.01×l0-6米D．0.101×l0-6米
二、填空题(每小题3分,共24分)
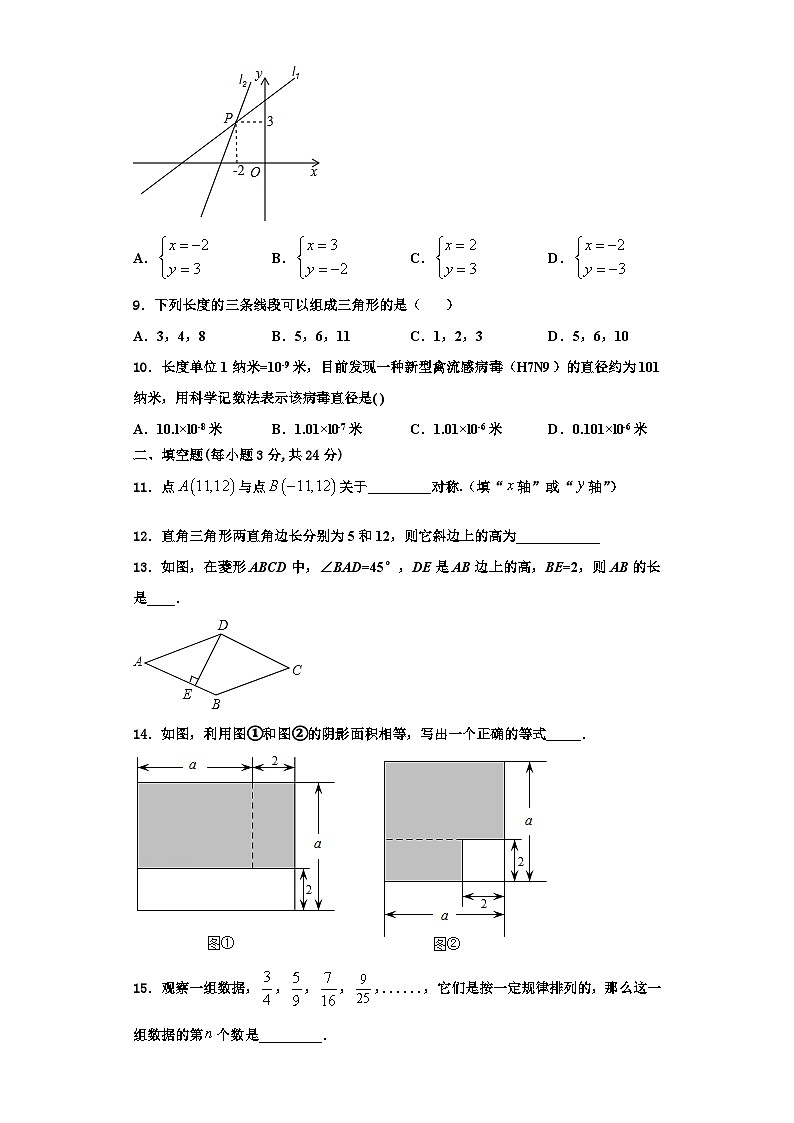
11．点与点关于_________对称.（填“轴”或“轴”）
12．直角三角形两直角边长分别为5和12，则它斜边上的高为____________
13．如图，在菱形ABCD中，∠BAD=45°，DE是AB边上的高，BE=2，则AB的长是____．
14．如图，利用图①和图②的阴影面积相等，写出一个正确的等式_____．
15．观察一组数据，，，，，．．．．．．，它们是按一定规律排列的，那么这一组数据的第个数是_________．
16．若数据的方差是，则数据的方差是__________．
17．一个正方形的边长增加2cm，它的面积就增加24cm，这个正方形的边长是______cm．
18．如图，已知AB∥CF，E为DF的中点．若AB＝13cm，CF＝7cm，则BD＝_____cm．
三、解答题(共66分)
19．（10分）随着智能手机的普及，微信抢红包已成为春节期间人们最喜欢的活动之一，某校七年级（1）班班长对全班50名学生在春节期间所抢的红包金额进行统计，并绘制成了统计图．请根据以上信息回答：
（1）该班同学所抢红包金额的众数是______，
中位数是______；
（2）该班同学所抢红包的平均金额是多少元？
​（3）若该校共有18个班级，平均每班50人，请你估计该校学生春节期间所抢的红包总金额为多少元？
20．（6分）如图1，在边长为3的等边中，点从点出发沿射线方向运动，速度为1个单位/秒，同时点从点出发，以相同的速度沿射线方向运动，过点作交射线于点，连接交射线于点．
（1）如图1，当时，求运动了多长时间？
（2）如图1，当点在线段（不考虑端点）上运动时，是否始终有？请说明理由；
（3）如图2，过点作，垂足为，当点在线段（不考虑端点）上时，的长始终等于的一半；如图3，当点运动到的延长线上时，的长是否发生变化？若改变，请说明理由；若不变，求出的长．
21．（6分）若在一个两位正整数N的个位数与十位数字之间添上数字5，组成一个新的三位数，我们称这个三位数为N的“至善数”，如34的“至善数”为354；若将一个两位正整数M加5后得到一个新数，我们称这个新数为M的“明德数”，如34的“明德数”为1．
（1）26的“至善数”是 ，“明德数”是 ．
（2）求证：对任意一个两位正整数A，其“至善数”与“明德数”之差能被45整除；
22．（8分）如图1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想.
(2)若三角尺GEF旋转到如图3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，(1)中的猜想还成立吗?若成立，请证明；若不成立，请说明理由.
23．（8分）按要求完成下列各题：
（1）计算：
（2）分解因式：
24．（8分）如图所示，小刚想知道学校的旗杆有多高，他发现旗杆上的绳子垂到地面还多了1．8m，当他把绳子下端拉开4m后，发现下端刚好接触地面，小刚算了算就知道了旗杆的高度．你知道他是怎样算出来的吗？
25．（10分）如图，，，、在上，，，求证：.
26．（10分）如图，∠BAD=∠CAE=90°，AB=AD，AE=AC．
（1）证明：BC=DE；
（2）若AC=13，CE经过点D，求四边形ABCD的面积．
参考答案
一、选择题(每小题3分,共30分)
1、B
【分析】结合题意，得，；结合＜，根据不等式的性质，得；再结合与y轴的交点，即可得到答案．
【详解】∵一次函数的图像经过点A（，1）和点B（，-3）
∴，
∴，
∵＜
∴
∴
∴选项A和C错误
当时，
∴选项D错误
故选：B．
【点睛】
本题考查了一次函数、不等式的知识；解题的关键是熟练掌握一次函数图像和不等式的性质，从而完成求解．
2、D
【分析】由△ABD≌△ACE，△ACE≌△ACM，△ABC是等边三角形可以对①②进行判断，由AC垂直平分EM和直角三角形的性质可对③进行判断，由△ADM是等边三角形可对④进行判断．
【详解】解：∵△ABC是等边三角形，
∴AB=AC，∠B=∠BAC=∠ACB=60°，
∵BD=CE，
∴△ABD≌△ACE（SAS）
∴AD=AE，∠BAD=∠CAE
∵线段沿翻折，
∴AE=AM，∠CAE=∠CAM，
∴，故①正确，
∴△ACE≌△ACM（SAS）
∴∠ACE=∠ACM=60°，故②正确，
由轴对称的性质可知，AC垂直平分EM，
∴∠CNE=∠CNM=90°，
∵∠ACM =60°，
∴∠CMN=30°，
∴在Rt△CMN中，，即，故③正确，
∵∠BAD=∠CAE，∠CAE=∠CAM，
∴∠BAD=∠CAM，
∵∠∠BAD+∠CAD=60°，
∴∠CAM +∠CAD=60°，
即∠DAM=60°，又AD=AM
∴△ADM为等边三角形，
∴故④正确，
所以正确的有4个，
故答案为：D．
【点睛】
本题考查了全等三角形的判定和性质、等边三角形的判定和性质、直角三角形的性质、线段垂直平分线的判定和性质、轴对称的性质等知识，解题的关键是灵活运用上述几何知识进行推理论证．
3、B
【分析】设原来的平均速度为x千米/时，高速公路开通后的平均速度为1.5x千米/时，根据走过相同的距离时间缩短了2小时，列方程即可．
【详解】解：设原来的平均速度为x千米/时，
由题意得，，
故选：B．
【点睛】
本题考查了由实际问题抽象出分式方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．
4、C
【分析】根据三角形的内角和和多边形的内角和即可得出答案.
【详解】∵六边形可分为4个三角形，每个三角形的内角和180°
∴m