重庆市万州第三中学2023-2024学年八年级数学第一学期期末复习检测试题【含解析】

这是一份重庆市万州第三中学2023-2024学年八年级数学第一学期期末复习检测试题【含解析】，共20页。试卷主要包含了考生要认真填写考场号和座位序号，约分的结果是等内容，欢迎下载使用。

注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题(每小题3分,共30分)
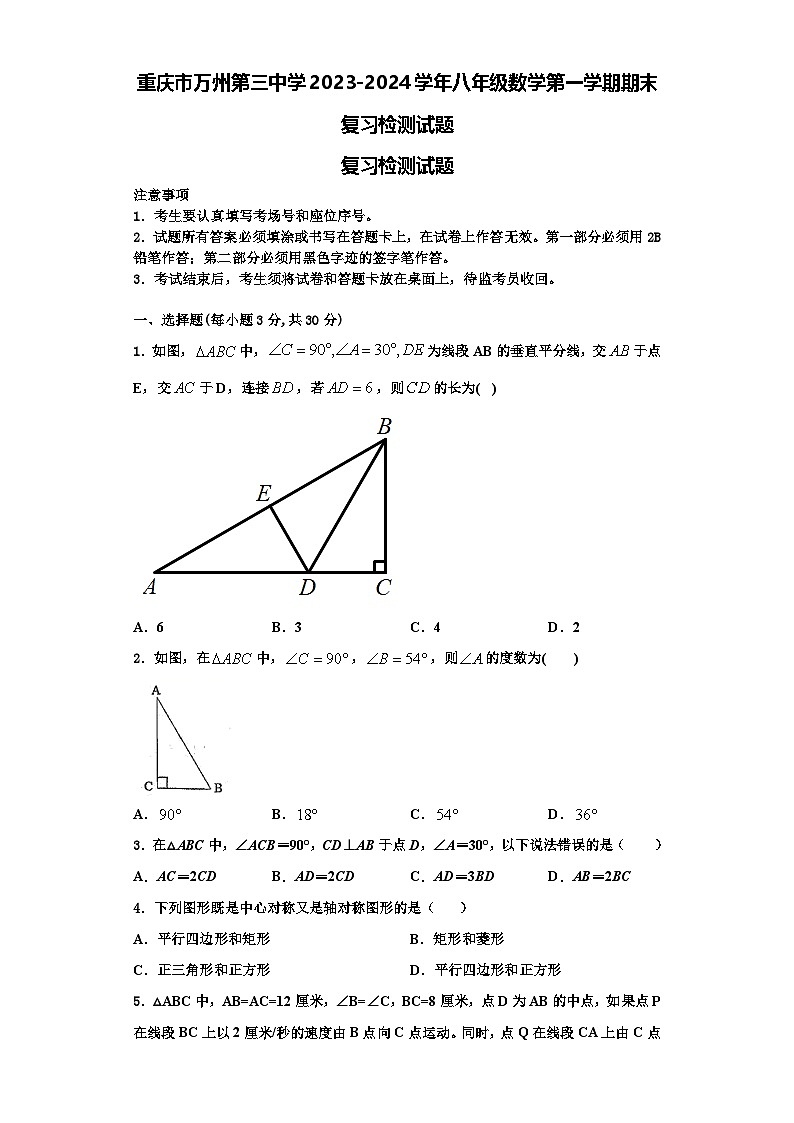
1．如图，中，为线段AB的垂直平分线，交于点E，交于D，连接，若，则的长为( )
A．6B．3C．4D．2
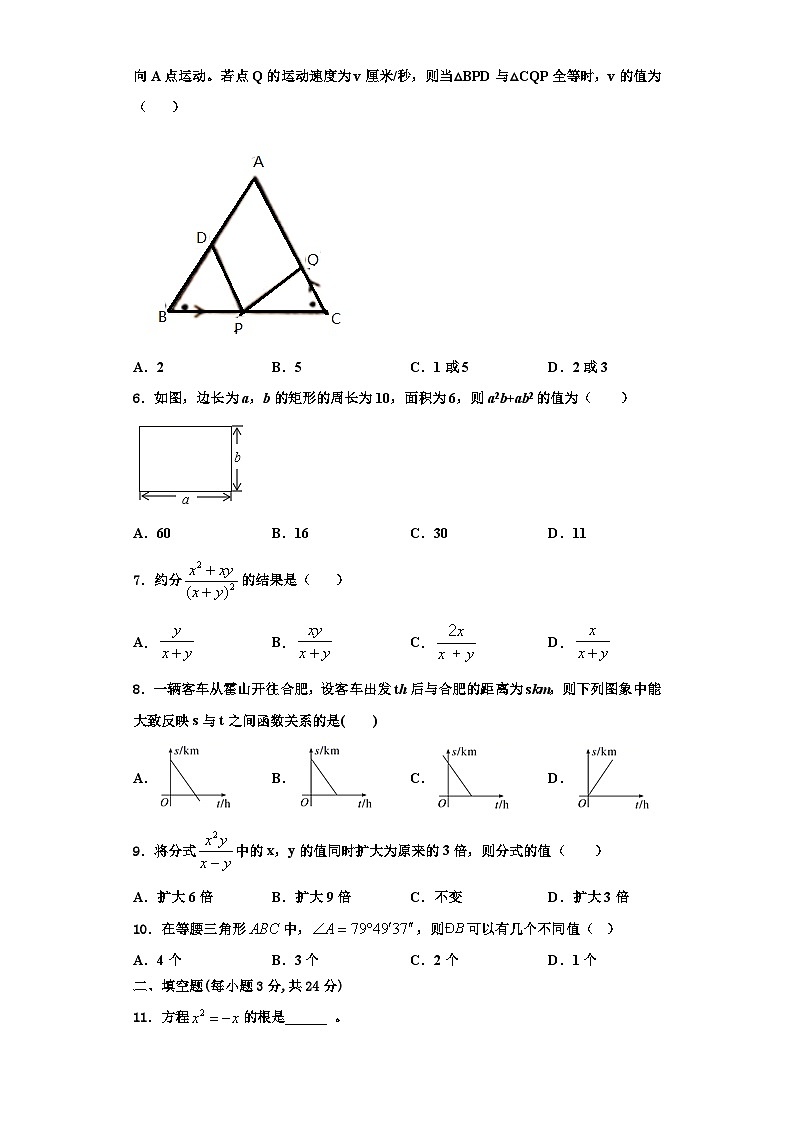
2．如图，在中，，，则的度数为( )
A．B．C．D．
3．在△ABC中，∠ACB＝90°，CD⊥AB于点D，∠A＝30°，以下说法错误的是（ ）
A．AC＝2CDB．AD＝2CDC．AD＝3BDD．AB＝2BC
4．下列图形既是中心对称又是轴对称图形的是（ ）
A．平行四边形和矩形B．矩形和菱形
C．正三角形和正方形D．平行四边形和正方形
5．△ABC中，AB=AC=12厘米，∠B=∠C，BC=8厘米，点D为AB的中点，如果点P在线段BC上以2厘米/秒的速度由B点向C点运动。同时，点Q在线段CA上由C点向A点运动。若点Q的运动速度为v厘米/秒，则当△BPD与△CQP全等时，v的值为（ ）
A．2B．5C．1或5D．2或3
6．如图，边长为a，b的矩形的周长为10，面积为6，则a2b+ab2的值为（ ）
A．60B．16C．30D．11
7．约分的结果是（ ）
A．B．C．D．
8．一辆客车从霍山开往合肥，设客车出发th后与合肥的距离为skm，则下列图象中能大致反映s与t之间函数关系的是( )
A．B．C．D．
9．将分式中的x，y的值同时扩大为原来的3倍，则分式的值（ ）
A．扩大6倍B．扩大9倍C．不变D．扩大3倍
10．在等腰三角形中，，则可以有几个不同值（ ）
A．4个B．3个C．2个D．1个
二、填空题(每小题3分,共24分)
11．方程的根是______ 。
12．如图，直线y=﹣x+3与坐标轴分别交于点A、B，与直线y=x交于点C，线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动，运动时间为t秒，连接CQ．若△OQC是等腰直角三角形，则t的值为_____．
13．如图，在中，，，垂足分别为，，，交于点．请你添加一个适当的条件，使≌．添加的条件是：____．（写出一个即可）
14．已知一个多边形的每一个内角都等于108°，则这个多边形的边数是 ．
15．把命题“在同一平面内，垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式为____________________________________________________．
16．在某中学举行的演讲比赛中，七年级5名参赛选手的成绩如下表所示，根据表中提供的数据，则3号选手的成绩为_____．
17．=_________
18．下图所示的网格是正方形网格，________．（填“”，“”或“”）
三、解答题(共66分)
19．（10分）解不等式组：，并把解集在数轴上表示出来.
20．（6分）计算：[（x2+y2）﹣（x﹣y）2+2y（x﹣y）]÷4y．
21．（6分）如图，在中，，点，，分别在边，，上，且，，连结，，，
（1）求证：．
（2）判断的形状，并说明理由．
（3）若，当_______时，．请说明理由．
22．（8分）先化简，再求值:
（1），其中；
（2），其中．
23．（8分）（1）计算：①；②
（2）解方程组：
24．（8分）解方程：
（1）4x2﹣8＝0；
（2）（x﹣2）3＝﹣1．
25．（10分）一辆汽车开往距离出发地200km的目的地，出发后第1小时内按原计划的速度匀速行驶，1小时后以原来速度的1.5倍匀速行驶，并比原计划提前30分钟到达目的地，求前1小时的行驶速度．
26．（10分）已知：在平面直角坐标系中，点为坐标原点，的顶点的坐标为，顶点在轴上(点在点的右侧)，点在上，连接，且．
(1)如图1，求点的纵坐标；
(2)如图2，点在轴上(点在点的左侧)，点在上，连接交于点；若，求证：
(3)如图3，在(2)的条件下，是的角平分线，点与点关于轴对称，过点作分别交于点，若，求点的坐标．
参考答案
一、选择题(每小题3分,共30分)
1、B
【分析】利用垂直平分线的性质得到AD=BD=6，∠A=∠ABD=30°，再根据∠C=90°得到∠CBD=30°，从而根据30°所对的直角边是斜边的一半得到结果.
【详解】解：∵DE垂直平分AB，
∴AD=BD=6，∠A=∠ABD=30°，
∵∠C=90°，
∴∠CBD=∠ABC-∠ABD=30°，
∴CD=BD=3，
故选B.
【点睛】
本题考查了垂直平分线的性质，含30°角的直角三角形的性质，解题的关键是熟练掌握含30°角的直角三角形的性质，即在直角三角形中，30°角所对的直角边等于斜边的一半．
2、D
【分析】由题意根据三角形内角和为180°进行分析计算，即可得解.
【详解】解：∵在中，，，
∴=180°-90°-54°=36°.
故选：D.
【点睛】
本题考查三角形内角和定理，熟练掌握三角形内角和为180°是解题关键，同时也可利用直角三角形两锐角互余进行分析.
3、B
【解析】在Rt△ABC 中，由∠A的度数求出∠B的度数，在Rt△BCD中，可得出∠BCD度数为30°，根据直角三角形中，30°所对的直角边等于斜边的一半，得到BC=2BD，由BD的长求出BC的长，在Rt△ABC中，同理得到AB=2BC，于是得到结论．
【详解】解：∵△ABC中，∠ACB＝90°，∠A＝30°，
∴AB＝2BC；
∵CD⊥AB，
∴AC＝2CD，
∴∠B＝60°，又CD⊥AB，
∴∠BCD＝30°，
在Rt△BCD中，∠BCD＝30°，CD＝BD，
在Rt△ABC中，∠A＝30°，AD＝CD＝3BD，
故选：B．
【点睛】
此题考查了含30°角直角三角形的性质，以及三角形的内角和定理，熟练掌握性质是解本题的关键．
4、B
【解析】根据轴对称图形与中心对称图形的概念求解．
【详解】A、矩形既是轴对称图形，也是中心对称图形，平行四边形不是轴对称图形，是中心对称图形．故错误；
B、矩形、菱形既是轴对称图形，也是中心对称图形．故正确；
C、等边三角形是轴对称图形，不是中心对称图形．故错误；
D、正方形既是轴对称图形，也是中心对称图形，平行四边形不是轴对称图形，是中心对称图形．故错误．
故选：B．
【点睛】
本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．
5、D
【分析】此题要分两种情况：①当BD=PC时，△BPD与△CQP全等，计算出BP的长，进而可得运动时间，然后再求v；②当BD=CQ时，△BDP≌△QCP，计算出BP的长，进而可得运动时间，然后再求v．
【详解】解：当BD=PC时，△BPD与△CQP全等，
∵点D为AB的中点，
∴BD=AB=6cm，
∵BD=PC，
∴BP=8-6=2（cm），
∵点P在线段BC上以2厘米/秒的速度由B点向C点运动，
∴运动时间时1s，
∵△DBP≌△PCQ，
∴BP=CQ=2cm，
∴v=2÷1=2；
当BD=CQ时，△BDP≌△QCP，
∵BD=6cm，PB=PC，
∴QC=6cm，
∵BC=8cm，
∴BP=4cm，
∴运动时间为4÷2=2（s），
∴v=6÷2=1（m/s）．
故v的值为2或1．
故选择：D．
【点睛】
此题主要考查了全等三角形的判定，关键是要分情况讨论，不要漏解，掌握全等三角形的判定方法：SSS、SAS、ASA、AAS、HL．
6、C
【分析】先把所给式子提公因式进行因式分解，整理为与所给周长和面积相关的式子，再代入求值即可．
【详解】∵矩形的周长为10，
∴a+b=5，
∵矩形的面积为6，
∴ab=6，
∴a2b+ab2=ab（a+b）=1．
故选：C．
【点睛】
本题既考查了对因式分解方法的掌握，又考查了代数式求值的方法，同时还隐含了整体的数学思想和正确运算的能力．
7、D
【分析】先将分式分子分母因式分解，再约去公因式即得．
【详解】解：
故选：D．
【点睛】
本题考查分式的基本性质的应用中的约分，找清楚分子分母的公因式是解题关键．
8、B
【解析】分析：因为匀速行驶，图象为线段，时间和路程是正数，客车从霍山出发开往合肥，客车与合肥的距离越来越近，路程由大变小，由此选择合理的答案．
详解：客车是匀速行驶的，图象为线段，s表示客车从霍山出发后与合肥的距离，s会逐渐减小为0；A、C、D都不符．
故选B．
点睛：本题主要考查了函数图象，解题时应首先看清横轴和纵轴表示的量，然后根据实际情况采用排除法求解．
9、B
【分析】将原式中的x、y分别用3x、3y代替，化简，再与原分式进行比较．
【详解】解：∵把分式中的x与y同时扩大为原来的3倍，
∴原式变为：＝ ＝9×，
∴这个分式的值扩大9倍．
故选：B．
【点睛】
本题考查了分式的基本性质．解题的关键是抓住分子、分母变化的倍数，解此类题首先把字母变化后的值代入式子中，然后约分，再与原式比较，最终得出结论．
10、B
【分析】根据等腰三角形的定义，∠A可能是底角，也可能是顶角，进行分类讨论即可．
【详解】解：①当∠A是顶角时，∠B=∠C=，
②当∠A为底角，∠B也为底角时， ，
③当∠A为底角，∠B为顶角时，∠B=，
故答案为：B．
【点睛】
本题考查了等腰三角形等边对等角的性质，涉及分类讨论问题，解题的关键是对∠A，∠B进行分类讨论．
二、填空题(每小题3分,共24分)
11、0或-1
【解析】由得+x=0,x(x+1)=0,x= 0或x=-1
故答案为：0或-1
12、2或4
【解析】先求出点C坐标，然后分为两种情况，画出图形，根据等腰三角形的性质求出即可.
【详解】∵由，得，
∴C（2，2）；
如图1，当∠CQO=90°，CQ=OQ，
∵C（2，2），
∴OQ=CQ=2，
∴t=2；
如图2，当∠OCQ=90°，OC=CQ，
过C作CM⊥OA于M，
∵C（2，2），
∴CM=OM=2，
∴QM=OM=2，
∴t=2+2=4，
即t的值为2或4，
故答案为2或4.

【点睛】
本题考查了一次函数与二元一次方程组、等腰直角三角形等知识，综合性比较强，熟练掌握相关知识、运用分类讨论以及数形结合思想是解题的关键.
13、AF=CB或EF=EB或AE=CE
【分析】根据垂直关系，可以判断△AEF与△CEB有两对对应角相等，就只需要找它们的一对对应边相等就可以了．
【详解】∵AD⊥BC，CE⊥AB，垂足分别为D、E，
∴∠BEC=∠AEC=∠ADB=∠ADC=90°，
∵∠B+∠BAD=90°，∠B+∠BCE =90°，
∴∠BAD=∠BCE，
所以根据AAS添加AF=CB或EF=EB；
根据ASA添加AE=CE．
可证△AEF≌△CEB．
故答案为：AF=CB或EF=EB或AE=CE．
【点睛】
本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关键．
14、1
【解析】试题分析：∵多边形的每一个内角都等于108°，∴每一个外角为72°．
∵多边形的外角和为360°，∴这个多边形的边数是：360÷÷72=1．
15、 “在同一平面内，如果两条直线都垂直于同一直线，那么这两直线互相平行”
【分析】命题题设为：在同一平面内，两条直线都垂直于同一条直线；结论为这两条直线互相平行．
【详解】“在同一平面内，垂直于同一条直线的两条直线互相平行”改写成“如果−−−，那么−−−”的形式为：“在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线互相平行”.
故答案为在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线互相平行.
16、1
【分析】先求出5名参赛选手的总成绩，再减去其它选手的成绩，即可得出3号选手的成绩．
【详解】解：∵观察表格可知5名选手的平均成绩为91分，
∴3号选手的成绩为91×5﹣90﹣95﹣89﹣88＝1（分）；
故答案为：1．
【点睛】
此题考查了算术平均数，掌握算术平均数的计算方法是解题的关键．
17、
【解析】首先把化（1.5）2019为×（）2018，再利用积的乘方计算（）2018×（）2018，进而可得答案．
【详解】原式＝（）2018×（）2018（）2018．
故答案为．
【点睛】
本题考查了积的乘方，关键是掌握（ab）n＝anbn（n是正整数）．
18、>
【分析】构造等腰直角三角形，根据等腰直角三角形的性质即可进行比较大小.
【详解】解：如下图所示，
是等腰直角三角形，
∴，
∴．
故答案为
另：此题也可直接测量得到结果．
【点睛】
本题考查等腰直角三角形的性质，构造等腰直角三角形是解题的关键.
三、解答题(共66分)
19、，把解集在数轴上表示见解析.
【解析】分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．
【详解】
解不等式①得：.
解不等式②得：.
将不等式解集表示在数轴如下：
得不等式组的解集为.
【点睛】
本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
20、x﹣y
【分析】首先利用完全平方公式计算小括号，然后再去括号，合并同类项，最后再计算除法即可．
【详解】解：原式＝（x2+y2﹣x2+2xy﹣y2+2xy﹣2y2）÷4y，
＝（4xy﹣2y2）÷4y，
＝x﹣y．
【点睛】
此题主要考查了整式的混合运算，关键是掌握计算顺序：有乘方、乘除的混合运算中，要按照先乘方后乘除的顺序运算，其运算顺序和有理数的混合运算顺序相似．
21、（1）见解析；（2）△ABC是等边三角形，理由见解析；（3），理由见解析
【分析】（1）根据等边对等角可证∠B＝∠C，然后利用SAS即可证出结论；
（2）根据全等三角形的性质可得∠BFD＝∠CDE，从而得出∠B＝∠1＝60°，然后根据等边三角形的判定定理即可得出结论；
（3）作FM⊥BC于M，利用30°所对的直角边是斜边的一半即可求出BM，从而求出BD．
【详解】（1）证明：∵AB＝AC，
∴∠B＝∠C，
在△BDF和△CED中，
，
∴△BDF≌△CED（SAS）；
（2）解：△ABC是等边三角形，理由如下：
由（1）得：△BDF≌△CED，
∴∠BFD＝∠CDE，
∵∠CDF＝∠B+∠BFD＝∠1+∠CDE，
∴∠B＝∠1＝60°，
∵AB＝AC，
∴△ABC是等边三角形
（3）解：当时，DF⊥BC，理由如下：
作FM⊥BC于M，如图所示：
由（2）得：△ABC是等边三角形，
∴∠B＝∠C＝60°，
∵FM⊥BC，
∴∠BFM＝30°，
∴，
∴，
∵
∴M与D重合，
∴时，DF⊥BC
故答案为：．
【点睛】
此题考查的是全等三角形的判定及性质、等边三角形的判定和直角三角形的性质，掌握全等三角形的判定及性质、等边三角形的判定和30°所对的直角边是斜边的一半是解决此题的关键．
22、（1），；（2），
【分析】（1）先运用完全平方公式与平方差公式展开，化简后再代入数据求值；
（2）先将括号内通分计算，再将除法变乘法，约分化简后代入数据求值．
【详解】（1）原式=
=
=
当时，
原式=
（2）原式=
=
=
=
当时，
原式=
【点睛】
本题考查了整式与分式的化简求值，熟练掌握整式乘法公式，以及分式的混合运算是解题的关键．
23、（1）①-2；②； （2）
【分析】（1）根据二次根式的运算法则即可求解；
（2）根据加减消元法即可求解．
【详解】（1）①
=
=
=3-5
=-2
②
=
=
（2）解
①×2得4x-2y=-8③
③-②得3y=15
解得y=5
把y=5代入①得2x-5=-4
解得x=
∴原方程组的解为．
【点睛】
此题主要考查二次根式与方程组的求解，解题的关键是熟知其运算法则．
24、（1）（2）
【分析】（1）方程整理后，利用平方根定义开方即可求出解；
（2）方程利用立方根定义开立方即可求出解．
【详解】解：（1）4x2﹣8＝0，
移项得：4x2﹣8＝0，即x2＝2，
开方得：；
（2）（x﹣2）3＝﹣1，
开立方得：x﹣2＝﹣1，
解得：x＝1．
【点睛】
本题主要考查一元二次方程的解法及立方根，熟练掌握运算法则是解题的关键．
25、原计划的行驶速度为80千米/时．
【分析】首先设原计划的行驶速度为x千米/时，根据题意可得等量关系：原计划所用时间实际所用时间=30分钟，根据等量关系列出方程，再解即可．
【详解】解：设原计划的行驶速度为x千米/时，由题意得：
，
解得：，
经检验：x=80是原分式方程的解．
答：原计划的行驶速度为80千米/时．
【点睛】
此题主要考查了分式方程的应用，关键是正确理解题意，表示出原计划所用时间和实际所用时间，根据时间关系列出分式方程．
26、（1）点的纵坐标为 1；（1）证明见解析；（3）点的坐标为．
【分析】（1）由得出，然后通过等量代换得出，则有，进而有，则点C的纵坐标可求；
（1）通过推导出，然后求出，则利用含30°的直角三角形的性质即可证明结论；
（3）连接，过点 作交 轴于点，先推出 ，然后通过垂直和角度之间的代换得出 则有 ，然后进一步，再因为 得出的值，则可求出 ，利用即可求出的值，则点E的坐标可求．
【详解】（1）如图 ，过点作于点


又



∴点的纵坐标为 1．
（1）


又


（3）如图 ，连接，过点作交轴于点


又

∵



∵点与点关于轴对称，点在轴上











∵点在轴上，且在点 的上方．
∴点的坐标为．
【点睛】
本题主要考查等腰三角形的性质，平行线的性质，含30°的直角三角形的性质，垂直平分线的性质，掌握等腰三角形的性质，平行线的性质，含30°的直角三角形的性质，垂直平分线的性质是解题的关键，第(3)问有一定的难度，主要是在于辅助线的作法．
选手
1号
2号
3号
4号
5号
平均成绩
得分
90
95
89
88
91