初中数学11.3.1 多边形优秀教案设计
展开【教材分析】
【教学流程】
教
学
目
标
知识
技能
1.了解多边形及有关概念,理解正多边形及其有关概念.
2.认识凸多边形,能辨别凸多边形.
过程
方法
通过类比三角形的概念归纳多边形的概念,能由实物中辨别寻找出几何图形,由几何图形联想或设计一些实物形状,丰富学生对几何图形的感性认识;
情感
态度
了解类比这种重要的数学学习方法,体验生活中处处有数学的道理.
重点
了解多边形及有关概念以及凸多边形的形状的辨别.
难点
正多边形的正确理解以及凸多边形的辨别.
环节
导 学 问 题
师 生 活 动
二次备课
情
境
引
入
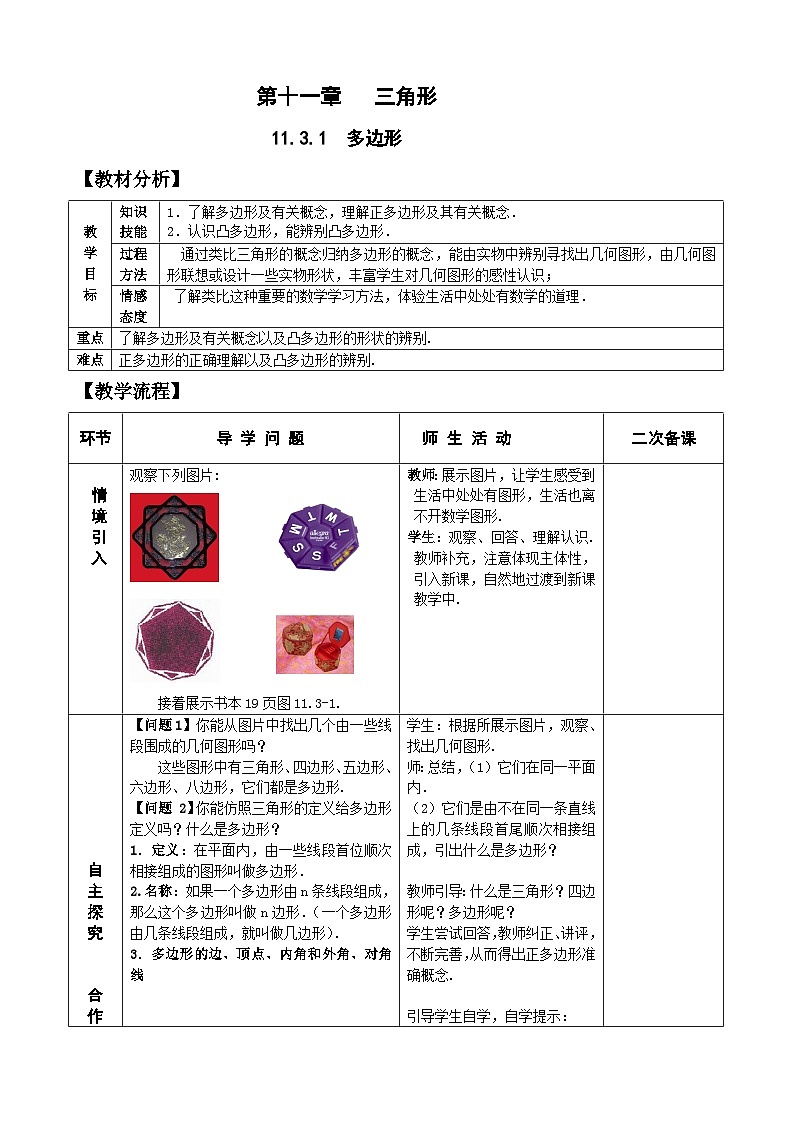
观察下列图片:
接着展示书本19页图11.3-1.
教师:展示图片,让学生感受到生活中处处有图形,生活也离不开数学图形.
学生:观察、回答、理解认识.
教师补充,注意体现主体性,引入新课,自然地过渡到新课教学中.
自
主
探
究
合
作
交
流
自
主
探
究
合
作
交
流
【问题1】你能从图片中找出几个由一些线段围成的几何图形吗?
这些图形中有三角形、四边形、五边形、六边形、八边形,它们都是多边形.
【问题 2】你能仿照三角形的定义给多边形定义吗?什么是多边形?
1.定义:在平面内,由一些线段首位顺次相接组成的图形叫做多边形.
2.名称:如果一个多边形由n条线段组成,那么这个多边形叫做n边形.(一个多边形由几条线段组成,就叫做几边形).
3.多边形的边、顶点、内角和外角、对角线
(1)内角 (2)外角 (3)对角线.
【问题 3】 多边形可以分为哪些的类型
1.凸多边形与凹多边形
整个多边形都在一条边所在直线的同一侧,这样的四边形叫做凸四边形,画出多边形任何一条边所在的直线,如果整个多边形都在这条直线的同一侧,这样的多边形称为凸多边形.
【问题 4】正多边形
各个角都相等,各条边都相等的多边形叫做正多边形.
学生:根据所展示图片,观察、找出几何图形.
师:总结,(1)它们在同一平面内.
(2)它们是由不在同一条直线上的几条线段首尾顺次相接组成,引出什么是多边形?
教师引导:什么是三角形?四边形呢?多边形呢?
学生尝试回答,教师纠正、讲评,不断完善,从而得出正多边形准确概念.
引导学生自学,自学提示:
什么是三角形的边、顶点、内角、外角?
由此可知什么是多边形的边、顶点、内角、外角?
对角线、凸四边形、正多边形的概念可通过学生看课本得出,组内交流,发表个人观点,然后展示,学生挑毛病逐渐完善、感知完成.
教师适当引导、或列举问题,引导学生思考、理解,加深认识,帮助学生准确掌握.
注意:
各边都相等、各角都相等同时具备才可以是正多边形.
尝
试
应
用
1.下列说法正确的个数有( )
(1)由四条线段首尾顺次相接组成的图形是四边形;
(2)各边都相等的多边形是正多边形;
(3)各角都相等的多边形不一定是正多边形;
(4)正多边形的各个外角都相等.
A.1个 B. 2个 C.3个 D.4个
2.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
3. 多边形的外角是( )
A. 内角的对顶角 B.内角的邻角
C.与内角有公共顶点的角 D.内角的邻补角
4.如图所示,这个多边形应记作什么?
过顶点A画这个多边形的对角线有几条?它们把多边形分成了几个三角形?这个多边形共有多少条对角线?
学生独立完成,组内交流,尝试得出结论,班内展示完成.
教师总结讲评,总结归纳得出结论:
参考答案:
1.A.
2.A.
3.D.
4.此多边形应记作五边形ABCDE,
过顶点A画这个多边形的对角线有2条,它们把五边形分成了三个三角形,
这个多边形共有5条对角线.
成
果
展
示
1.本节课你有哪些收获?你还有哪些疑惑?
2.你认为老师上课过程中还有哪些需要注意或改进的地方?
学生自我总结,谈体会及注意事项,
知识、规律总结、思想升华.
补
偿
提
高
2.(1)过四边形、五边形、六边形的一个顶点可以画出几条对角线?过n边形的一个顶点呢?
(2)四边形、五边形、六边形共有几条对角线?一个n边形共有几条对角线?
学生独立完成,组内讨论交流,班内展示.
教师讲评、总结,注意纠正.
(1)1,2,3,(n-3)条;
(2)2,5,9,条.
作
业
设
计
必做题:1.课本第21页 练习1、2题.
2.习题11.3第1题.
选做题:课本探究.
教师布置作业,并提出要求.
学生课下独立完成,延续课堂.
人教版八年级上册11.3.1 多边形教学设计: 这是一份人教版八年级上册11.3.1 多边形教学设计,共3页。教案主要包含了知识与技能,过程与方法,情感、态度与价值观,教学重点,教学难点,技巧点拨等内容,欢迎下载使用。
初中人教版11.3.1 多边形教案: 这是一份初中人教版11.3.1 多边形教案,共4页。
初中数学人教版八年级上册11.3.1 多边形教案: 这是一份初中数学人教版八年级上册11.3.1 多边形教案,共6页。教案主要包含了教材分析,学情分析,教学目标,教学重难点,教法与学法,教学准备,教学过程等内容,欢迎下载使用。













