初中数学人教版八年级上册11.3.2 多边形的内角和一等奖教案
展开【教材分析】
【教学流程】
教
学
目
标
知识
技能
了解多边形的外角定义,掌握多边形的外角和,能利用多边形的外角和是360°和多边形内角和公式解决问题.
过程
方法
1.通过推理论证等数学活动,探索多边形的外角和公式,感受数学思考过程的条理性,发展推理能力和语言表达能力.
2.利用多边形内角和与外角和公式解决实际问题,体会转化思想在几何中的运用.
情感
态度
通过观察、猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定性,提高学生学习热情.
重点
多边形的外角定义及多边形外角和公式的推导过程.
难点
综合运用多边形外角和、内角和公式解决数学问题.
环节
导 学 问 题
师 生 活 动
二次备课
情
境
引
入
【问题1】
大家清早跑步吗?小明每天坚持跑步,他怎样跑步呢?看大屏幕。
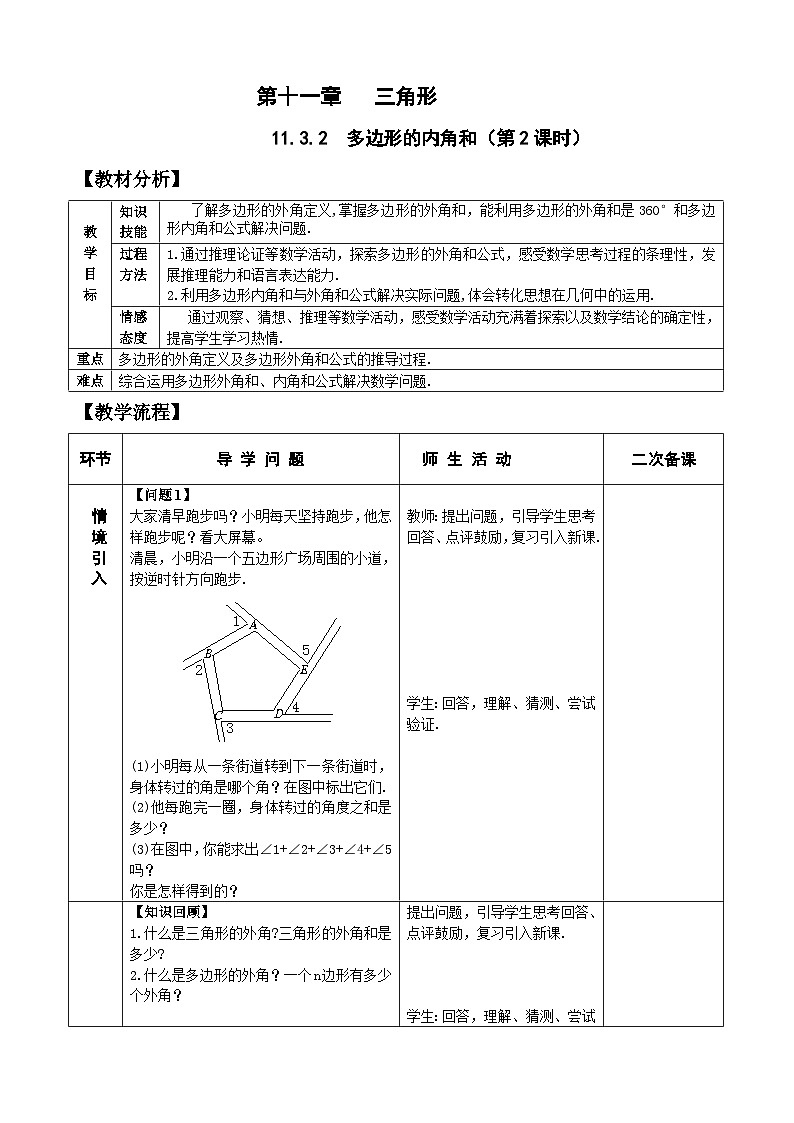
清晨,小明沿一个五边形广场周围的小道,按逆时针方向跑步.
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在图中,你能求出∠1+∠2+∠3+∠4+∠5吗?
你是怎样得到的?
教师:提出问题,引导学生思考回答、点评鼓励,复习引入新课.
学生:回答,理解、猜测、尝试验证.
自
主
探
究
合
作
交
流
自
主
探
究
合
作
交
流
【知识回顾】
1.什么是三角形的外角?三角形的外角和是多少?
2.什么是多边形的外角?一个n边形有多少个外角?
3.是否有多边形的外角和?多边形的外角和等于多少?
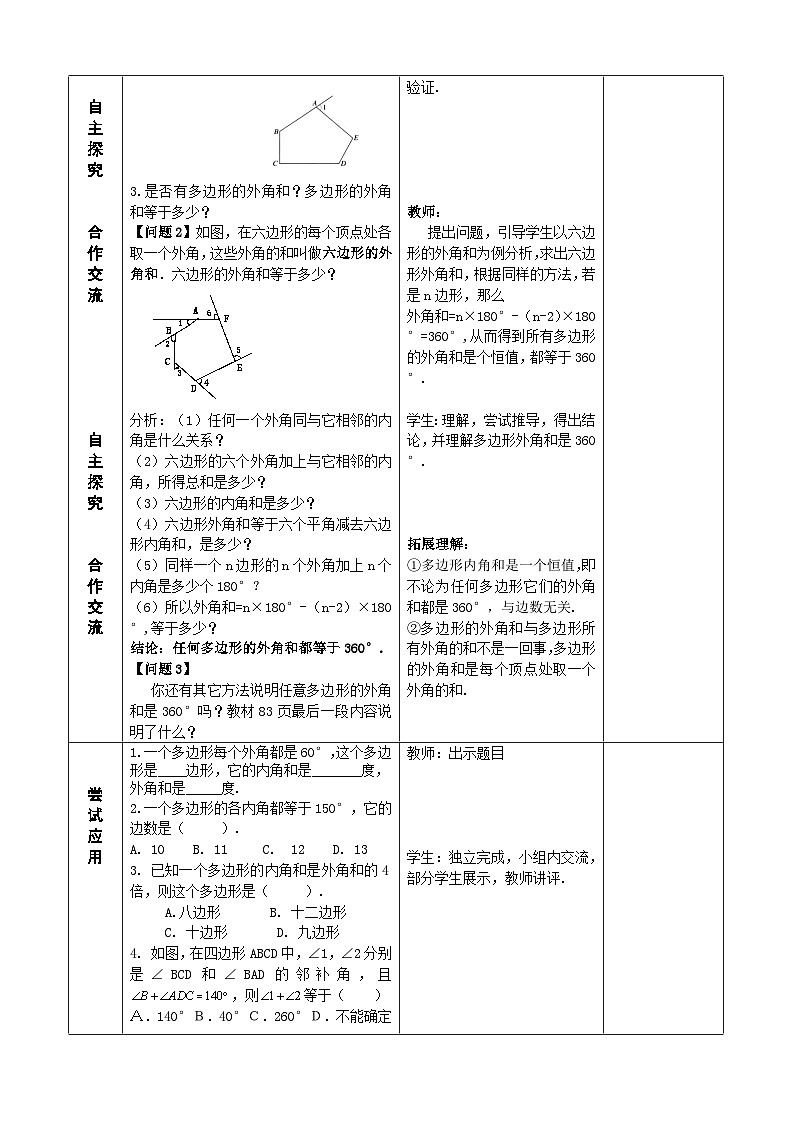
【问题2】如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
分析:(1)任何一个外角同与它相邻的内角是什么关系?
(2)六边形的六个外角加上与它相邻的内角,所得总和是多少?
(3)六边形的内角和是多少?
(4)六边形外角和等于六个平角减去六边形内角和,是多少?
(5)同样一个n边形的n个外角加上n个内角是多少个180°?
(6)所以外角和=n×180°-(n-2)×180°,等于多少?
结论:任何多边形的外角和都等于360°.
【问题3】
你还有其它方法说明任意多边形的外角和是360°吗?教材83页最后一段内容说明了什么?
提出问题,引导学生思考回答、点评鼓励,复习引入新课.
学生:回答,理解、猜测、尝试验证.
教师:
提出问题,引导学生以六边形的外角和为例分析,求出六边形外角和,根据同样的方法,若是n边形,那么
外角和=n×180°-(n-2)×180°=360°,从而得到所有多边形的外角和是个恒值,都等于360°.
学生:理解,尝试推导,得出结论,并理解多边形外角和是360°.
拓展理解:
①多边形内角和是一个恒值,即不论为任何多边形它们的外角和都是360°,与边数无关.
②多边形的外角和与多边形所有外角的和不是一回事,多边形的外角和是每个顶点处取一个外角的和.
尝
试
应
用
1.一个多边形每个外角都是60°,这个多边
形是____边形,它的内角和是_______度,
外角和是_____度.
2.一个多边形的各内角都等于150°,它的边数是( ).
A. 10 B. 11 C. 12 D. 13
3. 已知一个多边形的内角和是外角和的4倍,则这个多边形是( ).
A.八边形 B. 十二边形
C. 十边形 D. 九边形
4. 如图,在四边形ABCD中,∠1,∠2分别是∠BCD和∠BAD的邻补角,且,则等于( )
A.140°B.40°C.260°D.不能确定
5.在△ABC中,三外角之比为2:3:4,则与之对应的三内角度数比为( ).
A. 4:3:2 B. 5:3:1
C .3:2:4 D. 1:3:5
6.(2016•铜仁市)如果一个多边形的每一个外角都是60°,则这个多边形的边数是()
A. 3 B. 4 C. 5 D. 6
7.一个多边形的内角和等于它的外角和,这个多边形是( )
A .三角形 B. 四边形
C. 五边形 D. 六边形
8.(2015•北京)如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= 度.
教师:出示题目
学生:独立完成,小组内交流,部分学生展示,教师讲评.
参考答案:
1.六,720,360;
2.C 3.C 4.A
5.B 6.D
7.B 8.360
成
果
展
示
1. 三角形的外角和是多少?通过本节的学习你有哪些收获?
2. 方法:同顶点的每一个内角和外角互为邻补角是解决含内、外角问题的关键,是内、外角转换的纽带.
学生自我总结,畅谈体会和收获,梳理知识点,总结规律和应用方法.
补
偿
提
高
9.(2015•巴彦淖尔)如图,小明从A点
出发,沿直线前进12米后向左转36°,再
沿直线前进12米,又向左转36°…照这样
走下去,他第一次回到出发地A点时,一共
走了多少米.
学生尝试完成,教师巡视、指导,注意学生完成情况,讲评时总结、评价.
参考答案:
解:由题意得:360°÷36°=10,
则他第一次回到出发地A点时,一共走了12×10=120(米).
故答案为:120.
作
业
设
计
必做题:课本习题11.3,第 3、6、8题
选做题:完成探究.
教师布置作业,并提出要求.
学生课下独立完成,延续课堂.
人教版八年级上册11.3.2 多边形的内角和教学设计及反思: 这是一份人教版八年级上册11.3.2 多边形的内角和教学设计及反思,共3页。
初中数学人教版八年级上册第十一章 三角形11.3 多边形及其内角和11.3.1 多边形教案: 这是一份初中数学人教版八年级上册第十一章 三角形11.3 多边形及其内角和11.3.1 多边形教案,共3页。
初中数学人教版八年级上册11.3.2 多边形的内角和教学设计: 这是一份初中数学人教版八年级上册11.3.2 多边形的内角和教学设计,共9页。教案主要包含了问题等内容,欢迎下载使用。