初中数学人教版八年级上册12.1 全等三角形优秀教学设计

这是一份初中数学人教版八年级上册12.1 全等三角形优秀教学设计，共3页。教案主要包含了教材分析，教学流程等内容，欢迎下载使用。

【教材分析】
【教学流程】
教
学
目
标
知识
技能
掌握边角边公理的内容，能初步应用边角边公理判定两个三角形全等.
过程
方法
在图形变换以及实际操作的过程中发展学生的空间观念，形成几何直觉和识图能力，通过观察、猜想、验证、推理、交流等数学活动进一步发展演绎推理能力和发散思维能力．
情感
态度
通过探究三角形全等的条件的活动，提高观察分析图形的能力及运算能力，养成乐于探索的良好品质.
重点
掌握“SAS”来判定三角形全等，进一步证明线段相等，角相等．
难点
正确地书写证明过程，恰当地选择判定定理．
环节
导 学 问 题
师 生 活 动
二次备课
情
境
引
入
复习:
1．如何判定三角形全等？
2．有没有其他判定全等的方法呢？
师提问，学生回答后师板书课题.
自
主
探
究
合
作
交
流
自
主
探
究
合
作
交
流
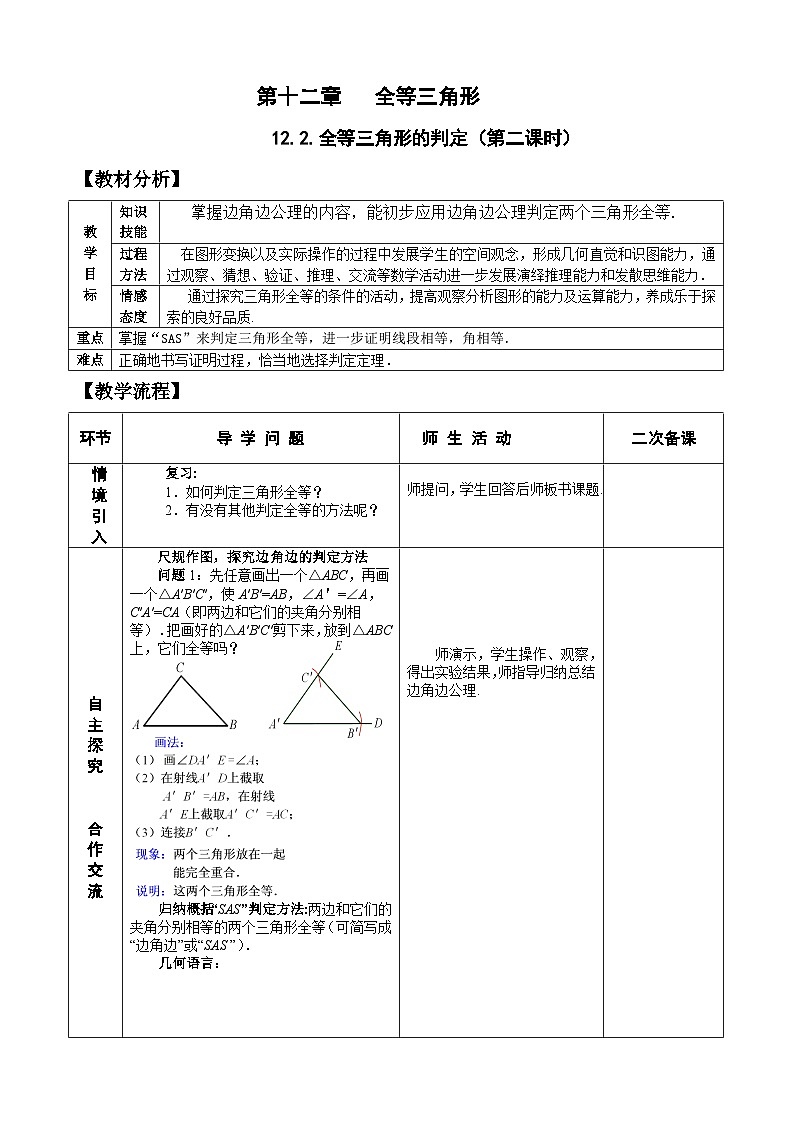
尺规作图，探究边角边的判定方法
问题1：先任意画出一个△ABC，再画一个△A′B′C′，使A′B′=AB，∠A＇=∠A，C′A′=CA（即两边和它们的夹角分别相等）．把画好的△A′B′C′剪下来，放到△ABC 上，它们全等吗？

归纳概括“SAS”判定方法:两边和它们的夹角分别相等的两个三角形全等（可简写成“边角边”或“SAS ”）．
几何语言：
例题讲解，学会运用
例：如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个不经过池塘可以直接到达点A 和B的点C，连接AC并延长至D，使CD =CA，连接BC 并延长至E，使CE =CB，连接ED，那么量出DE的长就是A，B的距离．为什么？
探索“SSA”能否识别两三角形全等
问题2：两边一角分别相等包括“两边夹角”和“两边及其中一边的对角”分别相等两种情况，前面已探索出“SAS”判定三角形全等的方法，那么由“SSA”的条件能判定两个三角形全等吗？
操作：画△ABC 和△DEF，使∠B =∠E =30°， AB =DE=5 cm ，AC =DF =3 cm ．观察所得的两个三角形是否全等？
解：两边和其中一边的对角这三个条件无法唯一确定三角形的形状，所以不能保证两个三角形全等．因此，△ABC 和△DEF 不一定全等．
师演示，学生操作、观察，得出实验结果，师指导归纳总结边角边公理.
先引导学生分析题目，再出现过程，
学生动手操作，并画图，小组合作探究并汇报研究结果.
学生画图后回答问题.
尝
试
应
用
1．下图中全等的三角形有（ ）
图1 图2 图3 图4
A．图1和图2 B．图2和图3
C．图2和图4 D．图1和图3
2．已知：如图，OA＝OB，OC平分∠AOB，求证：△AOC≌△BOC.
3．如图，C为BE上一点，点A，D分别在BE两侧．AB∥ED，AB＝CE，BC＝ED.求证：△ABC≌△CED.

教师出示题目
学生先自主探究
合作交流
学生展示
师生评价，纠错
1.D
2.证明：∵OC平分∠AOB，
∴∠AOC＝∠BOC.
在△AOC和△BOC中，
eq \b\lc\{(\a\vs4\al\c1(OA＝OB，,∠AOC＝∠BOC（已证），,OC＝OC（公共边），))
∴△AOC≌△BOC(SAS)．
证明：∵AB∥ED，
∴∠B＝∠E.
在△ABC和△CED中，eq \b\lc\{(\a\vs4\al\c1(AB＝CE，,∠B＝∠E，,BC＝ED，))
∴△ABC≌△CED(SAS)．
成
果
展
示
课堂小结：
谈谈你的收获和体会
学生回答，师归纳补充.
形成知识体系
补
偿
提
高
4．如图，D，E分别是△ABC的边AB，AC的中点，点F在DE的延长线上，且EF＝DE，求证：
(1)BD＝FC；
(2)AB∥CF.

教师出示题目
学生先自主探究
合作交流学生展示
师生评价，纠错
证明：(1)∵E是AC的中点，
∴AE＝CE.
在△ADE和△CFE中，eq \b\lc\{(\a\vs4\al\c1(AE＝CE，,∠AED＝∠CEF，,DE＝FE，))
∴△ADE≌△CFE(SAS)．
∴AD＝CF.
∵D是AB的中点，
∴AD＝BD.
∴BD＝FC.
由(1)知△ADE≌△CFE，
∴∠A＝∠ECF.
∴AB∥CF.
作
业
设
计
课后作业:
教科书习题12.2第2、3、10题．

学生课后独立完成.