高教版（2021·十四五）基础模块 下册5.5 指数函数与对数函数的应用导学案

这是一份高教版（2021·十四五）基础模块 下册5.5 指数函数与对数函数的应用导学案，文件包含串讲02对数与对数函数考点串讲原卷版docx、串讲02对数与对数函数考点串讲解析版docx等2份学案配套教学资源，其中学案共24页， 欢迎下载使用。
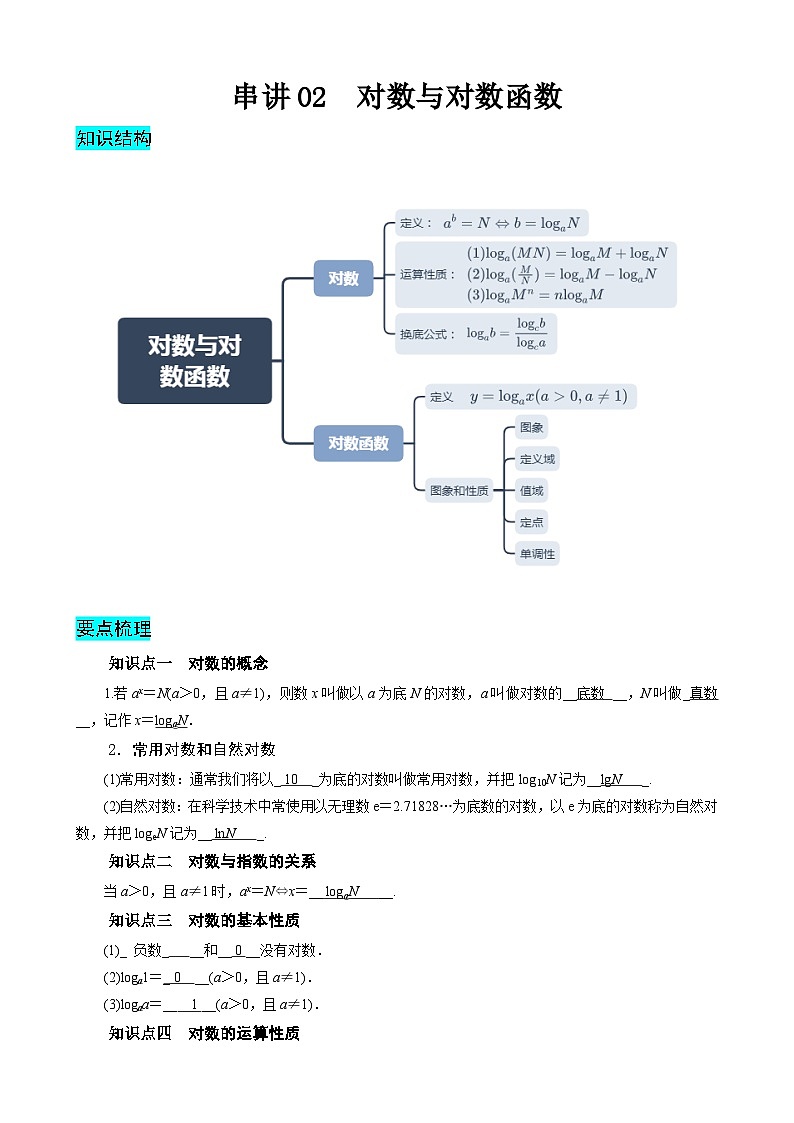
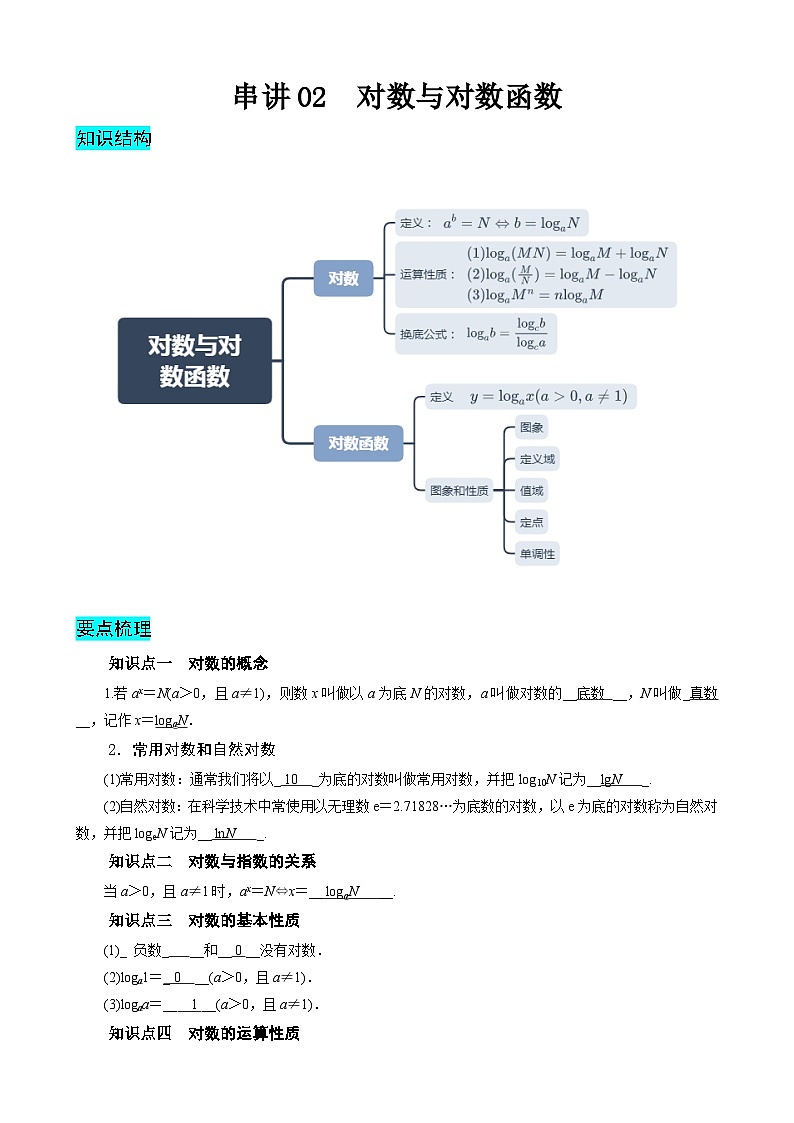
要点梳理
知识点一 对数的概念
1.若ax＝N(a＞0，且a≠1)，则数x叫做以a为底N的对数，a叫做对数的__底数 __，N叫做_真数 __，记作x＝lgaN．
2．常用对数和自然对数
(1)常用对数：通常我们将以_ 10 _为底的对数叫做常用对数，并把lg10N记为__lgN _.
(2)自然对数：在科学技术中常使用以无理数e＝2.71828…为底数的对数，以e为底的对数称为自然对数，并把lgeN记为__ lnN _.
知识点二 对数与指数的关系
当a＞0，且a≠1时，ax＝N⇔x＝__ lgaN __.
知识点三 对数的基本性质
(1)_ 负数_ __和__ 0 __没有对数．
(2)lga1＝_ 0 __(a＞0，且a≠1)．
(3)lgaa＝__ 1 __(a＞0，且a≠1)．
知识点四 对数的运算性质
知识点五 换底公式
若a>0，且a≠1；b>0；c>0，且c≠1，则有lgab＝eq \f(lgcb,lgca)．
知识点六 对数函数
函数y＝lgax(a>0，且a≠1)叫做对数函数，其中x是自变量，定义域是(0，＋∞)．
知识点七 对数函数的图象及性质
题型探究：
考点一 对数定义与性质的应用
例1. 有以下四个结论，其中正确的是（ ）
A．B．
C．若，则D．若，则
【答案】B
【分析】利用对数的性质判断AB；利用指数式与对数式的互化判断CD.
【详解】对于A，由于，而0和负数没有对数，则无意义，A错误；
对于B，，B正确；
对于C，由，得，C错误；
对于D，由，得，D错误.
故选：B
例2. 方程的解是（ ）
A．1B．2C．eD．3
【答案】D
【分析】利用指数与对数的转化即可得到结果.
【详解】∵，∴，∴.
故选：D.
『规律方法』 (1)任意实数的奇次方根只有一个，正数的偶次方根有两个且互为相反数；
(2)(eq \r(n,a))n是实数a的n次方根的n次幂，其中实数a的取值由n的奇偶性决定．
【归纳提升】 对数性质在计算中的应用
(1)对数运算时的常用性质：lgaa＝1，lga1＝0.
(2)使用对数的性质时，有时需要将底数或真数进行变形后才能运用；对于多重对数符号的，可以先把内层视为整体，逐层使用对数的性质．
【变式】1. 有以下四个结论，其中正确的是（ ）
A．B．
C．若，则D．
【答案】B
【分析】根据对数的性质，逐项判断，即可得出结果.
【详解】因为，，所以A错误，B正确；若，则，故C错误；，而没有意义，故D错误．
故选：B.
2. 求下列各式中x的值：
(1)x＝ eq lg\s\d8(\f(1,2)) 16； (2)lg8x＝－eq \f(1,3)
【解析】 (1)∵x＝ eq lg\s\d8(\f(1,2)) 16，∴(eq \f(1,2))x＝16，即2－x＝24.∴－x＝4，即x＝－4.
(2)∵lg8x＝－eq \f(1,3)，∴x＝8－ eq \s\up7(\f(1,3)) ＝eq \f(1,\r(3,8))＝eq \f(1,2).
考点二 对数的运算性质的应用
例3．用lgax，lgay，lgaz表示：
(1)lga(xy2)；(2)lga(xeq \r(y))；(3)lgaeq \r(3,\f(x,yz2)).
[解析] (1)lga(xy2)＝lgax＋lgay2＝lgax＋2lgay.
(2)lga(xeq \r(y))＝lgax＋lgaeq \r(y)＝lgax＋eq \f(1,2)lgay.
(3)lgaeq \r(3,\f(x,yz2))＝eq \f(1,3)lgaeq \f(x,yz2)＝eq \f(1,3)[lgax－lga(yz2)]
＝eq \f(1,3)(lgax－lgay－2lgaz)．
例4. 化简或求值：
（1）．
【详解】（1）原式(2)
【详解】（2）
[归纳提升] 1.对对数式进行计算、化简时，一要注意准确应用对数的性质和运算性质．二要注意取值范围对符号的限制．
2. 利用对数运算性质化简与求值的原则和方法
(1)基本原则：
①正用或逆用公式，对真数进行处理，②选哪种策略化简，取决于问题的实际情况，一般本着便于真数化简的原则进行．
(2)两种常用的方法：
①“收”，将同底的两对数的和(差)收成积(商)的对数；
②“拆”，将积(商)的对数拆成同底的两对数的和(差)．
【变式探究】1. 用lgax、lgay、lgaz表示下列各式：
(1)lga(x3y5)； (2)lgaeq \f(\r(x),yz).
[解析] (1)lga(x3y5)＝lgax3＋lgay5
＝3lgax＋5lgay.
(2)lgaeq \f(\r(x),yz)＝lgaeq \r(x)－lga(yz)
＝lgaxeq \s\up6(\f(1,2))－(lgay＋lgaz)
＝eq \f(1,2)lgax－lgay－lgaz.
2. 计算下列各式：
(1)eq \f(1,2)lgeq \f(32,49)－eq \f(4,3)lgeq \r(8)＋lgeq \r(245)；
(2)lg25＋eq \f(2,3)lg8＋lg5×lg20＋(lg2)2.
[解析] (1)法一：原式＝eq \f(1,2)(5lg2－2lg7)－eq \f(4,3)×eq \f(3,2)lg2＋eq \f(1,2)(2lg7＋lg5)
＝eq \f(5,2)lg2－lg7－2lg2＋lg7＋eq \f(1,2)lg5
＝eq \f(1,2)lg2＋eq \f(1,2)lg5＝eq \f(1,2)(lg2＋lg5)
＝eq \f(1,2)lg10＝eq \f(1,2).
法二：原式＝lgeq \f(4\r(2),7)－lg4＋lg7eq \r(5)
＝lgeq \f(4\r(2)×7\r(5),7×4)
＝lg(eq \r(2)·eq \r(5))＝lgeq \r(10)＝eq \f(1,2).
(2)原式＝2lg5＋2lg2＋lg5×(2lg2＋lg5)＋(lg2)2
＝2lg10＋(lg5＋lg2)2＝2＋(lg10)2
＝2＋1＝3.
考点三 换底公式的应用
例5. 计算：
(1)
(2)
【答案】(1)；
(2)4.
【分析】（1）（2）根据给定条件，利用对数运算性质及换底公式计算作答.
【详解】（1）.
（2）.
[归纳提升] 关于换底公式的用途和本质：
(1)换底公式的本质是化异底为同底，这是解决对数问题的基本方法．
(2)在运用换底公式时，若能结合底数间的关系恰当选用一些重要的结论，如lgab＝eq \f(1,lgba)；lgaan＝n，lgambn＝eq \f(n,m)lgab；lg2＋lg5＝1等，将会达到事半功倍的效果．
【变式】利用对数的换底公式计算：
(1)；
(2)．
【答案】(1)
(2)
【分析】根据换底公式和对数的运算性质计算即可.
【详解】（1）
；
（2）
.
考点五 对数函数的定义域
例6. 函数的定义域是 .
【答案】
【分析】根据函数特征得到不等式，求出定义域
【详解】由题意得，解得，
故定义域为.
故答案为：
例7. 函数的定义域为 .
【答案】
【分析】利用对数函数真数大于零，解不等式即可求得结果.
【详解】由对数函数定义可得，解得或，
所以函数定义域为.
故答案为：
[归纳提升] 定义域是研究函数的基础，若已知函数解析式求定义域，常规为：①分母不能为零，②0的零次幂与负指数次幂无意义，③偶次方根的被开方式(数)非负，④求与对数函数有关的函数定义域时，除遵循前面求函数定义域的方法外，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意底数；三是按底数的取值应用单调性．
【变式探究】1. 函数的定义域为
【答案】
【分析】由对数及分式的性质列不等式组求定义域即可.
【详解】由解析式知：或，
所以函数定义域为.
故答案为：
2．函数的定义域为 ．
【答案】
【分析】利用函数有意义，列出不等式求解即得.
【详解】函数有意义，则，解得，
所以函数的定义域为.
故答案为：
考点六 利用对数函数的单调性比较大小
例8. 比较下列各组中两个值的大小：
(1)ln0.3，ln2；
(2)lga3.1，lga5.2(a＞0，且a≠1)；
(3)lg30.2，lg40.2；
[分析] (1)底数相同时如何比较两个对数值的大小？
(2)底数不同、真数相同时如何比较两个对数值的大小？
[解析] (1)因为函数y＝lnx在(0，＋∞)上是增函数，且0.3＜2，所以ln0.3＜ln2.
(2)当a＞1时，函数y＝lgax在(0，＋∞)上是增函数，
又3.1＜5.2，所以lga3.1＜lga5.2；当0＜a＜1时，函数y＝lgax在(0，＋∞)上是减函数，又3.1＜5.2，所以lga3.1＞lga5.2.
(3)因为0＞lg0.23＞lg0.24，所以eq \f(1,lg0.23)＜eq \f(1,lg0.24)，
即lg30.2＜lg40.2.
[归纳提升] 比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性．
(2)同真数的利用对数函数的图象或用换底公式转化．
(3)若底数为同一参数，则根据底数对对数函数单调性的影响，对底数进行分类讨论．
提醒：比较数的大小时先利用性质比较出与0或1的大小．
【变式探究】1. 比较大小： （填“>”或“