




湘教版(2019)必修 第一册第3章 函数的概念与性质3.1 函数优秀课件ppt
展开那对于一般函数而言,如何定义函数的零点呢?这是我们本节课该研究的内容。
与二次函数的零点一样,对于一般函数y=f(x),我们把使f(x)=0的实数x叫作函数y=f(x)的零点。零点不是点!
所以说求f(x)=0的实数根,就确定了函数y=f(x)的零点。对于不能用公式法求根的方程f(x)=0,我们可以把它与函数y=f(x)联系起来,利用函数的性质找出零点,从而求方程的根。
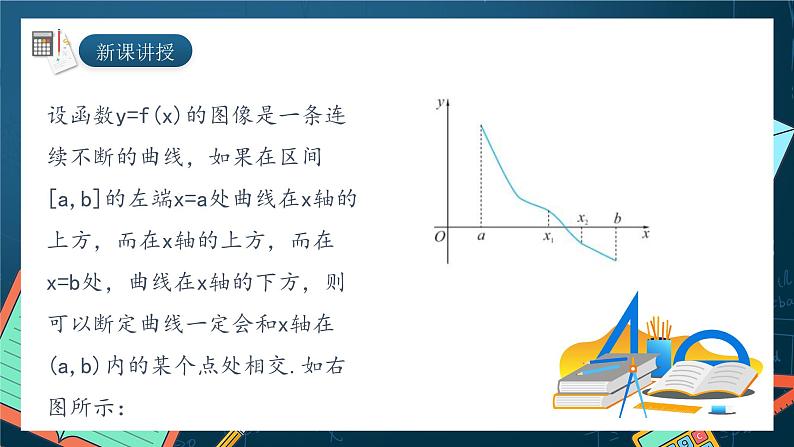
设函数y=f(x)的图像是一条连续不断的曲线,如果在区间[a,b]的左端x=a处曲线在x轴的上方,而在x轴的上方,而在x=b处,曲线在x轴的下方,则可以断定曲线一定会和x轴在(a,b)内的某个点处相交.如右图所示:
若知道y=f(x)在区间[a,b]上单调递增或递减,则可以进一步的断定,方程f(x)=0在(a,b)内恰有一根,即函数y=f(x)在(a,b)内只有一个零点。
判断零点个数我们有四种常用的办法:[1]利用方程根,转化为解方程,方程有几个不同的实数根就有几个零点;[2]画出函数y=f(x)的图像,判断它与x轴有几个交点,从而判定零点的个数;[3]结合单调性,利用零点存在性定理,可判断y=f(x)在(a,b)上零点的个数;[4]转化成两个函数图像交点的问题。
所以可以判断出它有一个零点。
解:由于 f(1)=-3<0 f(2)=11>0 且该函数是一个连续函数,所以根据“零点存在性定理”知f(x)在(1,2)上存在零点;又因为该函数单调递增,所以说, f(x)在(1,2)上仅有一个零点。
解: y=f(x)+a有两个零点等价于f(x)=-a有两个交点。先画出f(x)的图像,如图所示:
解:f(0)=d=0 f(1)=a+b+c=0 f(-1)=-a+b-c<0 两式一加得:2b<0所以b<0
数学必修 第一册4.4.1 对数函数的概念课堂教学课件ppt: 这是一份数学必修 第一册<a href="/sx/tb_c4053120_t3/?tag_id=26" target="_blank">4.4.1 对数函数的概念课堂教学课件ppt</a>,共21页。PPT课件主要包含了教学目标,学科素养,知识回顾,指数函数的图像,新知探索,拓展提升,归纳总结,SumUp,课后作业等内容,欢迎下载使用。
高中数学湘教版(2019)必修 第一册3.1 函数精品ppt课件: 这是一份高中数学湘教版(2019)必修 第一册3.1 函数精品ppt课件,文件包含441方程的根与函数的零点doc、441方程的根与函数的零点pptx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
必修 第一册4.4 函数与方程课文内容ppt课件: 这是一份必修 第一册4.4 函数与方程课文内容ppt课件,文件包含湘教版高中数学必修第一册第4章44441方程的根与函数的零点课件ppt、湘教版高中数学必修第一册第4章44441方程的根与函数的零点学案doc、湘教版高中数学必修第一册课后素养落实34方程的根与函数的零点含答案doc等3份课件配套教学资源,其中PPT共44页, 欢迎下载使用。













