黑龙江省鸡西市部分学校2023-2024学年八年级下学期期中考试数学试卷(含答案)

这是一份黑龙江省鸡西市部分学校2023-2024学年八年级下学期期中考试数学试卷(含答案)，共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列式子中一定是二次根式的是( )
A.B.C.D.
2．下列计算正确的是( )
A.B.
C.D.
3．若三角形的三边分别为a，b，c，则下面四种情况中，构成直角三角形的是( )
A.，，B.，，
C.，，D.，，
4．下面说法正确的个数有( )
①如果三角形三个内角的比是，那么这个三角形是直角三角形；
②如果三角形的一个外角等于与它相邻的一个内角，则这么三角形是直角三角形；
③如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形；
④如果，那么是直角三角形；
⑤若三角形的一个内角等于另两个内角之差，那么这个三角形是直角三角形；
⑥在中，若，则此三角形是直角三角形
A.3个B.4个C.5个D.6个
5．如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则为( )
A.75°B.60°C.55°D.45°
6．下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
7．如图，在平行四边形ABCD中，，AE平分交BC于点E，交AE于点F，则( )
A.40°B.50°C.60°D.80°
8．顺次连接平行四边形四边的中点所得的四边形是( )
A.矩形B.菱形C.正方形D.平行四边形
9．如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于C、D，则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
A.矩形B.菱形C.正方形D.等腰梯形
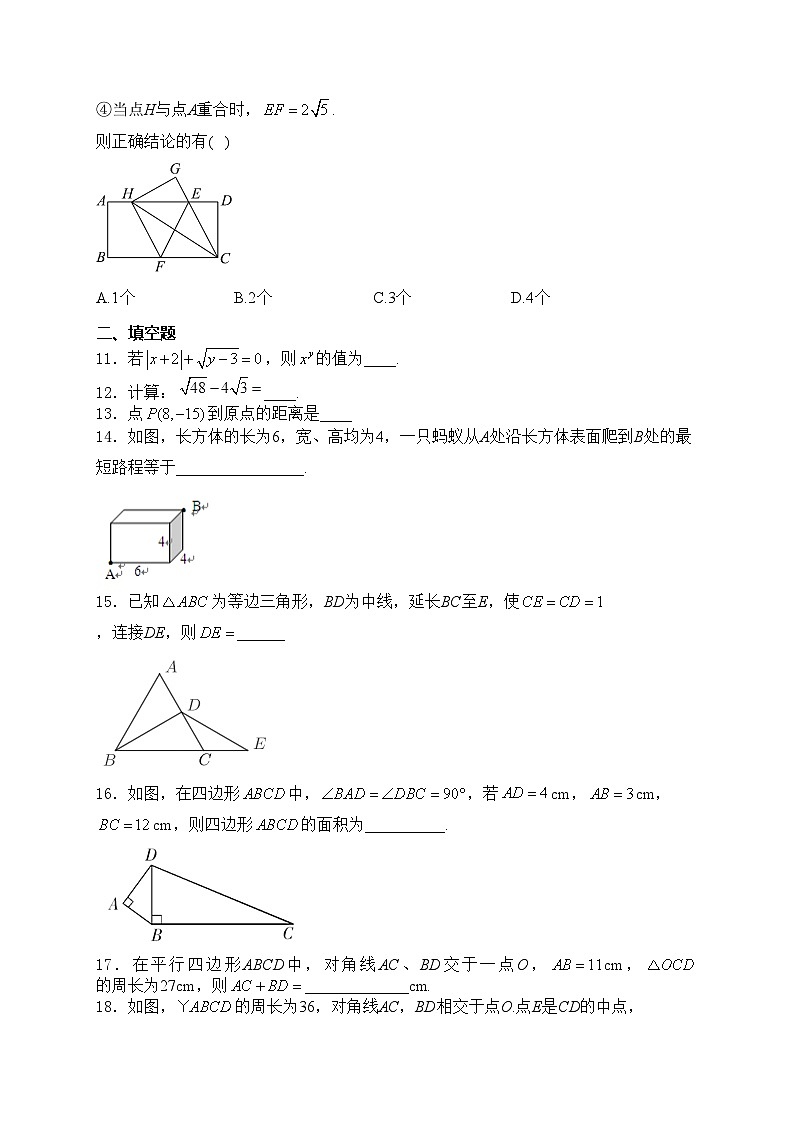
10．如图，矩形纸片中，，，点E，F分别在，上，将纸片沿直线折叠，点C落在上的点H处，点D落在点G处，有以下四个结论：
①四边形是菱形；
②平分；
③线段的取值范围为；
④当点H与点A重合时，.
则正确结论的有( )
A.1个B.2个C.3个D.4个
二、填空题
11．若，则的值为____.
12．计算：____.
13．点到原点的距离是____
14．如图，长方体的长为6，宽、高均为4，一只蚂蚁从A处沿长方体表面爬到B处的最短路程等于________________.
15．已知为等边三角形，BD为中线，延长BC至E，使，连接DE，则______
16．如图，在四边形中，，若cm，cm，cm，则四边形的面积为__________.
17．在平行四边形ABCD中，对角线AC、BD交于一点O，cm，的周长为27cm，则_____________cm.
18．如图，的周长为36，对角线AC，BD相交于点O.点E是CD的中点，，则的周长为_____.
19．如图，把一张矩形纸片ABCD沿对角线BD折叠，使C点落在，且与AD交于E点，若，则_____.
20．如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作第三个正方形AEGH，如此下去….若正方形ABCD的边长记为，按上述方法所作的正方形的边长依次为，，，…，，则________.
三、解答题
21．计算：
(1)；
(2).
22．如图，，，，交于点G，点E、F分别为，的中点，连接，.
(1)求证：四边形是平行四边形；
(2)当点G是中点时，求证：四边形是菱形.
23．学完勾股定理之后，同学们想利用升旗的绳子、卷尺，测算出学校旗杆的高度.爱动脑筋的小明这样设计了一个方案：将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端5米处，发现此时绳子底端距离打结处约1米.请你设法帮小明算出旗杆的高度.
24．如图，飞机在空中水平飞行，某一时刻刚好飞到一男孩子头顶上方4000米处，过了20秒，飞机距离这个男孩头顶5000米.飞机每小时飞行多少千米？
25．正方形网格中每个小正方形的边长都是1，每个小正方形的顶点叫做格点，以格点为顶点.
(1)在图①中，画一个面积为10的正方形；
(2)在图②、③中，分别画两个不全等的直角三角形，使它们的三边长都是无理数.
26．如图，四边形ABCD是平行四边形，E，F是对角线BD上的点，.
求证：(1)；
(2).
27．如图，在矩形ABCD中，已知对角线AC、BD相交于点O，E是CD中点，连接OE，过点C作交线段OE的延长线于点F，连接DF.
(1)求证：；
(2)求证：四边形ODFC是菱形.
28．(1)如图①，在正方形中，的顶点E，F分别在，边上，高与正方形的边长相等，求的度数.
(2)如图②，在中，，，点M，N是边上的任意两点，且，将绕点A逆时针旋转至位置，连接，试判断，，之间的数量关系，并说明理由.
参考答案
1．答案：B
解析：A、当时，不是二次根式，故本选项错误；
B、一定是二次根式，故本选项正确；
C、当时，不是二次根式，故本选项错误；
D、当时，不是二次根式，故本选项错误；
故选：B.
2．答案：C
解析：A、与不是同类二次根式，不能合并，本选项不符合题意；
B、，本选项不符合题意；
C、，本选项符合题意；
D、，本选项不符合题意；
故选：C.
3．答案：B
解析：A、，C、，D、，故错误；
B、，能构成直角三角形，本选项正确.
故选：B.
4．答案：D
解析：①∵三角形三个内角的比是，
∴设三角形的三个内角分别为x，2x，3x，
，解得，
，
∴此三角形是直角三角形，故本小题正确；
②∵三角形的一个外角与它相邻的一个内角的和是180°，
∴若三角形的一个外角等于与它相邻的一个内角，则此三角形是直角三角形，故本小题正确；
③∵直角三角形的三条高的交点恰好是三角形的一个顶点，
∴若三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形，故本小题正确；
④，
∴设，则，
，解得，
，
∴此三角形是直角三角形，故本小题正确；
⑤∵三角形的一个外角等于与它不相邻的两内角之和，三角形的一个内角等于另两个内角之差，
∴三角形一个内角也等于另外两个内角的和，
∴这个三角形中有一个内角和它相邻的外角是相等的，且外角与它相邻的内角互补，
∴有一个内角一定是90°，故这个三角形是直角三角形，故本小题正确；
⑥∵三角形的一个外角等于与它不相邻的两内角之和，又一个内角也等于另外两个内角的和，
由此可知这个三角形中有一个内角和它相邻的外角是相等的，且外角与它相邻的内角互补，
∴有一个内角一定是90°，故这个三角形是直角三角形，故本小题正确.
故选：D.
5．答案：B
解析：∵四边形ABCD是正方形，
，，，
是等边三角形，
，，
，
，
；
故选：B.
6．答案：B
解析：A、一组邻边相等的平行四边形是菱形，故选项错误；
B、有一个角是直角的平行四边形是矩形，正确；
C、对角线垂直的平行四边形是菱形，故选项错误；
D、两组对边平行的四边形才是平行四边形，故选项错误.
故选：B.
7．答案：B
解析：，，
.
∵AE平分
.
.
故选：B.
8．答案：D
解析：顺次连接四边形四边的中点所得的四边形是平行四边形，
如果原四边形的对角线互相垂直，那么所得的四边形是矩形，
如果原四边形的对角线相等，那么所得的四边形是菱形，
如果原四边形的对角线相等且互相垂直，那么所得的四边形是正方形，
因为平行四边形的对角线不一定相等或互相垂直，因此得平行四边形.
故选：D.
9．答案：B
解析：∵分别以A和B为圆心，大于的长为半径画弧，两弧相交于C、D，
，
∴四边形ADBC一定是菱形，
故选：B.
10．答案：C
解析：①根据图形折叠的性质可知，，
∵，
∴.
∴.
∴.
∴.
又，
∴四边形是平行四边形.
又，
∴四边形是菱形.
说法①正确.
②∵四边形是菱形，
∴.
若平分，则，
∴.
所以，只有当时，平分.
说法②错误.
③如图所示，当点A与点H重合时，可以取得最小值.
设，则.
在中
，即
解得
所以，的最小值为3.
当四边形为正方形时，可以取得最大值.
此时点E、G、D重合，.
所以，的最大值为4.
综上所述，.
说法③正确.
④根据题意可知，
∵四边形是菱形.
∴，.
∴.
∴.
说法④正确.
综上所述，说法正确的为①③④.
故选：C.
11．答案：
解析：∵，，，
∴，，
解得，，
∴.
12．答案：0
解析：原式.
故答案为：0.
13．答案：17
解析：到原点的距离是.
故答案为：17.
14．答案：10
解析：将长方体展开，蚂蚁从A处沿长方体表面爬到B处的最短路程转化为两点之间线段最短，分情况讨论：(1)当前面和上面组成一个平面时，则这个长方形的长和宽分别是8和6，则所走的最短线段是；(2)当左面与上面组成一个长方形时，则这个长方形的长和宽分别是10和4，所以走的最短线段是；(3)当前面和右面组成一个长方形时，则这个长方形的长和宽分别是10和4，所以走的最短线段是，因为，所以最短路程为10.
15．答案：
解析：∵等边三角形每个内角都等于60°，
，
又，
.
如图，过点C作于点F，
，
∴在中，
.
16．答案：36
解析：，cm，cm
().
故答案为：36.
17．答案：32
解析：∵四边形ABCD是平行四边形，
cm，，，
的周长为27cm，
cm，
，，
cm，
故答案为：32.
18．答案：15
解析：的周长为36，
，则.
∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，，
.
又∵点E是CD的中点，
∴OE是的中位线，.
.
的周长，即的周长为15.
故答案是：15.
19．答案：25°
解析：∵四边形ABCD是矩形，
，，
，
，
根据折叠可得，
，
，
，
故答案为：25°.
20．答案：
解析：，且在直角中，，
，
同理，
；
由此可知：
，，；…
故找到规律.
21．答案：(1)
(2)
解析：(1)
；
(2)
.
22．答案：(1)见解析
(2)见解析
解析：(1)∵，
∴四边形是平行四边形，，
∴，
∵E、F分别为，的中点，
∴，，即，
∵，
∴四边形是平行四边形.
(2)如图：连接，
∵四边形是平行四边形，
∴，
∵G为中点，
∴，
∵，
∴四边形是平行四边形，
∴，
∵，
∴，
∵F为中点，
∴，即，
∵四边形是平行四边形，
∴四边形是菱形.
23．答案：12米
解析：设旗杆长为x米，则绳长为米，则由勾股定理可得：
，
解得，
答：旗杆的高度为12米.
24．答案：
解析：如图，
由题意得，米，，米，由勾股定理得(米)，
所以飞机飞行的速度为(千米/小时)
25．答案：(1)作图见解析
(2)作图见解析
解析：(1)如图①所示：
(2)如图②③所示.
26．答案：证明见解析
解析：(1)∵四边形ABCD是平行四边形，
，，
，
，
，
在和中，
，
(AAS)，
；
(2)由(1)得，
，
，
，
∴四边形AECF是平行四边形，
.
27．答案：(1)见解析
(2)见解析
解析：证明：(1)，
，
∵E是CD中点，
，
在和中，
，
；
(2)，
，
，
∴四边形ODFC是平行四边形，
在矩形ABCD中，，
∴四边形ODFC是菱形.
28．答案：(1)
(2).理由见解析
解析：(1)在和中，，
∴.
∴.
同理：.
∵，
∴
(2)，理由如下：
∵将绕点A逆时针旋转至位置，
∴，，
∴.
∴.
又∵，
∴.
∴.
∵，
∴.
∴.
∴，即.