最新高考数学一轮复习-第五章-平面向量及其应用、复数【导学案】

这是一份最新高考数学一轮复习-第五章-平面向量及其应用、复数【导学案】，共62页。
课程标准
1.了解平面向量的实际背景，理解平面向量的意义和两个向量相等的含义．
2．理解平面向量的几何表示和基本要素．
3．掌握平面向量加、减运算及运算规则，理解其几何意义．
4．掌握平面向量数乘运算及运算规则，理解其几何意义．理解两个平面向量共线的含义．
5．了解平面向量的线性运算性质及其几何意义．
[由教材回扣基础]
1．向量的有关概念
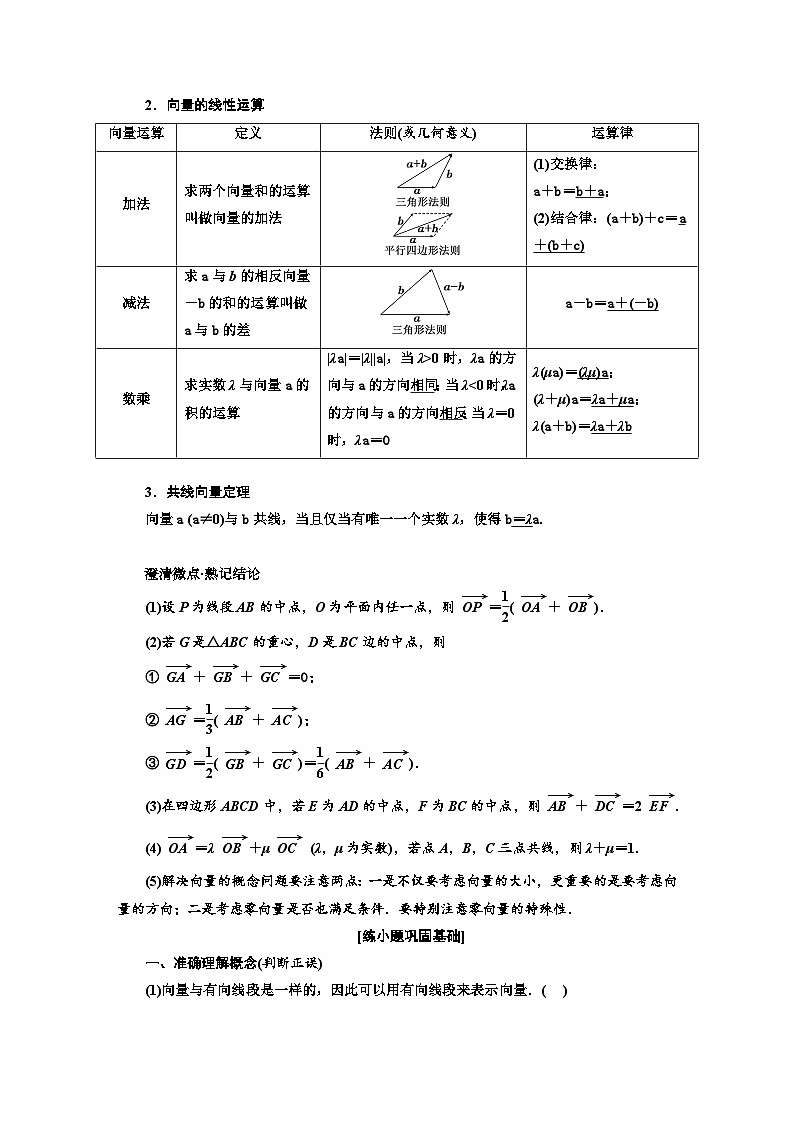
2．向量的线性运算
3．共线向量定理
向量a (a≠0)与b共线，当且仅当有唯一一个实数λ，使得b＝λa.
eq \a\vs4\al(澄清微点·熟记结论)
(1)设P为线段AB的中点，O为平面内任一点，则eq \(OP,\s\up7(―→))＝eq \f(1,2)(eq \(OA,\s\up7(―→))＋eq \(OB,\s\up7(―→)))．
(2)若G是△ABC的重心，D是BC边的中点，则
①eq \(GA,\s\up7(―→))＋eq \(GB,\s\up7(―→))＋eq \(GC,\s\up7(―→))＝0；
②eq \(AG,\s\up7(―→))＝eq \f(1,3)(eq \(AB,\s\up7(―→))＋eq \(AC,\s\up7(―→)))；
③eq \(GD,\s\up7(―→))＝eq \f(1,2)(eq \(GB,\s\up7(―→))＋eq \(GC,\s\up7(―→)))＝eq \f(1,6)(eq \(AB,\s\up7(―→))＋eq \(AC,\s\up7(―→)))．
(3)在四边形ABCD中，若E为AD的中点，F为BC的中点，则eq \(AB,\s\up7(―→))＋eq \(DC,\s\up7(―→))＝2eq \(EF,\s\up7(―→)).
(4)eq \(OA,\s\up7(―→))＝λeq \(OB,\s\up7(―→))＋μeq \(OC,\s\up7(―→)) (λ，μ为实数)，若点A，B，C三点共线，则λ＋μ＝1.
(5)解决向量的概念问题要注意两点：一是不仅要考虑向量的大小，更重要的是要考虑向量的方向；二是考虑零向量是否也满足条件．要特别注意零向量的特殊性．
[练小题巩固基础]
一、准确理解概念(判断正误)
(1)向量与有向线段是一样的，因此可以用有向线段来表示向量．( )
(2)若向量eq \(AB,\s\up7(―→))与向量eq \(CD,\s\up7(―→))是共线向量，则A，B，C，D四点在一条直线上．( )
(3)当两个非零向量a，b共线时，一定有b＝λa，反之成立．( )
答案：(1)× (2)× (3)√
二、练牢教材小题
1．(湘教版必修②P11T3)化简：eq \(AB,\s\up7(―→))＋eq \(DA,\s\up7(―→))＋eq \(BD,\s\up7(―→))－eq \(BC,\s\up7(―→))－eq \(CA,\s\up7(―→))＝________.
答案：eq \(AB,\s\up7(―→))
2．(人教B版必修②P143例2改编)已知|a|＝1，|b|＝2，则|3a＋2b|的最大值和最小值分别为________．
答案：7,1
3．(人教A版必修②P14例6改编)已知▱ABCD的对角线AC和BD相交于点O，且eq \(OA,\s\up7(―→))＝a，eq \(OB,\s\up7(―→))＝b，则eq \(DC,\s\up7(―→))＝________，eq \(BC,\s\up7(―→))＝________.(用a，b表示)
答案：b－a －a－b
4．(人教A版必修②P15T2)点C在线段AB上，且eq \f(AC,CB)＝eq \f(5,2)，则eq \(AC,\s\up7(―→))＝________eq \(AB,\s\up7(―→))，eq \(BC,\s\up7(―→))＝________eq \(AB,\s\up7(―→)).
答案：eq \f(5,7) －eq \f(2,7)
三、练清易错易混
1．(忽视零向量)下列命题中，正确的是( )
A．a与b共线，b 与c共线，则a与c共线
B．向量a与b平行，则a与b的方向相同或相反
C．两个共同起点且相等的向量，其终点必相同
D．零向量与任意数的乘积都为零
答案：C
2．(忽视向量相等的条件)若四边形ABCD满足eq \(AD,\s\up7(―→))∥eq \(BC,\s\up7(―→))且|eq \(AB,\s\up7(―→))|＝|eq \(DC,\s\up7(―→))|，则四边形ABCD的形状是______________．
解析：当|eq \(AD,\s\up7(―→))|＝|eq \(BC,\s\up7(―→))|时，四边形ABCD是平行四边形；当|eq \(AD,\s\up7(―→))|≠|eq \(BC,\s\up7(―→))|时，四边形ABCD是等腰梯形．
答案：平行四边形或等腰梯形
命题视角一 平面向量的基本概念(自主练通)
1．设a是非零向量，λ是非零实数，下列结论中正确的是( )
A．a与λa的方向相反
B．a与λ2a的方向相同
C．|－λa|≥|a|
D．|－λa|≥|λ|a
解析：选B 对于A，当λ＞0时，a与λa的方向相同，当λ＜0时，a与λa的方向相反；B正确；对于C，|－λa |＝|－λ|| a |，由于|－λ|的大小不确定，故|－λa |与| a的大小关系不确定；对于D，|λ| a是向量，而|－λa |表示长度，两者不能比较大小．
2．(多选)下列命题为真命题的是( )
A．若a与b为非零向量，且a∥b，则a＋b必与a或b平行
B．若e为单位向量，且a∥e，则a＝|a|e
C．两个非零向量a，b，若|a－b|＝|a|＋|b|，则a与b共线且反向
D．“两个向量平行”是“这两个向量相等”的必要不充分条件
答案：ACD
3.如图，等腰梯形ABCD中，对角线AC与BD交于点P，点E，F分别在两腰AD，BC上，EF过点P，且EF∥AB，则下列等式成立的是( )
A．eq \(AD,\s\up7(―→))＝eq \(BC,\s\up7(―→)) B．eq \(AC,\s\up7(―→))＝eq \(BD,\s\up7(―→))
C．eq \(PE,\s\up7(―→))＝eq \(PF,\s\up7(―→)) D．eq \(EP,\s\up7(―→))＝eq \(PF,\s\up7(―→))
解析：选D 根据相等向量的定义，A中，eq \(AD,\s\up7(―→))与eq \(BC,\s\up7(―→))的方向不同，故A错误；B中，eq \(AC,\s\up7(―→))与eq \(BD,\s\up7(―→))的方向不同，故B错误；C中，eq \(PE,\s\up7(―→))与eq \(PF,\s\up7(―→))的方向相反，故C错误；D中，eq \(EP,\s\up7(―→))与eq \(PF,\s\up7(―→))的方向相同，且长度都等于线段EF长度的一半，故D正确．
[一“点”就过]
解决向量问题的关键点
(1)相等向量具有传递性，非零向量的平行也具有传递性．
(2)相等向量不仅模相等，而且方向也相同，所以相等向量一定是平行向量，但平行向量未必是相等向量．
(3)向量可以平移，平移后的向量与原向量是相等向量．解题时，不要把它与函数图象的平移混为一谈．
(4)eq \f(a,| a |)是非零向量a方向上的单位向量，因此单位向量eq \f(a,| a |)与a方向相同．
命题视角二 平面向量的线性运算
考法(一) 平面向量的线性运算
[例1] (1)(2020·新高考Ⅱ卷)若D为△ABC的边AB的中点，则eq \(CB,\s\up7(―→))＝( )
A．2eq \(CD,\s\up7(―→))－eq \(CA,\s\up7(―→)) B．2eq \(CA,\s\up7(―→))－eq \(CD,\s\up7(―→))
C．2eq \(CD,\s\up7(―→))＋eq \(CA,\s\up7(―→)) D．2eq \(CA,\s\up7(―→))＋eq \(CD,\s\up7(―→))
(2)在四边形ABCD中，AB∥CD，AB＝3DC，E为BC的中点，则eq \(AE,\s\up7(―→))等于( )
A.eq \f(2,3)eq \(AB,\s\up7(―→))＋eq \f(1,2)eq \(AD,\s\up7(―→))
B.eq \f(1,2)eq \(AB,\s\up7(―→))＋eq \f(2,3)eq \(AD,\s\up7(―→))
C.eq \f(5,6)eq \(AB,\s\up7(―→))＋eq \f(1,3)eq \(AD,\s\up7(―→))
D.eq \f(1,3)eq \(AB,\s\up7(―→))＋eq \f(5,6)eq \(AD,\s\up7(―→))
[解析] (1)∵D为△ABC的边AB的中点，∴eq \(CD,\s\up7(―→))＝eq \f(1,2)(eq \(CA,\s\up7(―→))＋eq \(CB,\s\up7(―→)))，∴eq \(CB,\s\up7(―→))＝2eq \(CD,\s\up7(―→))－eq \(CA,\s\up7(―→)).故选A.
(2)由eq \(BC,\s\up7(―→))＝eq \(BA,\s\up7(―→))＋eq \(AD,\s\up7(―→))＋eq \(DC,\s\up7(―→))＝－eq \f(2,3)eq \(AB,\s\up7(―→))＋eq \(AD,\s\up7(―→))，得eq \(AE,\s\up7(―→))＝eq \(AB,\s\up7(―→))＋eq \(BE,\s\up7(―→))＝eq \(AB,\s\up7(―→))＋eq \f(1,2)eq \(BC,\s\up7(―→))＝eq \(AB,\s\up7(―→))＋eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(eq \(AD,\s\up7(―→))－\f(2,3)eq \(AB,\s\up7(―→)) ))＝eq \f(2,3)eq \(AB,\s\up7(―→))＋eq \f(1,2)eq \(AD,\s\up7(―→)).故选A.
[答案] (1)A (2)A
[方法技巧]
向量线性运算的解题策略
(1)常用的法则是平行四边形法则和三角形法则，一般共起点的向量求和用平行四边形法则，求差用三角形法则，求首尾相连的向量的和用三角形法则．
(2)用基本向量表示某个向量问题的基本技巧：①观察各向量的位置；②寻找相应的三角形或多边形；③运用法则找关系；④化简结果．
考法(二) 利用向量的线性运算求参数
[例2] (2022·韶关模拟)在△ABC中，点M为AC上的点，且eq \(AM,\s\up7(―→))＝eq \f(1,2)eq \(MC,\s\up7(―→))，若eq \(BM,\s\up7(―→))＝λeq \(BA,\s\up7(―→))＋μeq \(BC,\s\up7(―→))，则λ－μ的值是( )
A．1 B.eq \f(1,2) C.eq \f(1,3) D.eq \f(2,3)
[解析] 由eq \(AM,\s\up7(―→))＝eq \f(1,2)eq \(MC,\s\up7(―→))，得eq \(AM,\s\up7(―→))＝eq \f(1,3)eq \(AC,\s\up7(―→))，所以eq \(BM,\s\up7(―→))＝eq \(BA,\s\up7(―→))＋eq \(AM,\s\up7(―→))＝eq \(BA,\s\up7(―→))＋eq \f(1,3)eq \(AC,\s\up7(―→))＝eq \(BA,\s\up7(―→))＋eq \f(1,3)(eq \(BC,\s\up7(―→))－eq \(BA,\s\up7(―→)))＝eq \f(2,3)eq \(BA,\s\up7(―→))＋eq \f(1,3)eq \(BC,\s\up7(―→))，又因为eq \(BM,\s\up7(―→))＝λeq \(BA,\s\up7(―→))＋μeq \(BC,\s\up7(―→))，所以λ＝eq \f(2,3)，μ＝eq \f(1,3)，故λ－μ＝eq \f(1,3).故选C.
[答案] C
[方法技巧]
利用向量的线性运算求参数的方法
与向量的线性运算有关的参数问题，一般是构造三角形，利用向量线性运算的三角形法则进行加法或减法运算，然后通过建立方程组即可求得相关参数．
[针对训练]
1．在△ABC中，D为AB的中点，点E满足eq \(EB,\s\up7(―→))＝4eq \(EC,\s\up7(―→))，则eq \(ED,\s\up7(―→))＝( )
A.eq \f(5,6)eq \(AB,\s\up7(―→))－eq \f(4,3)eq \(AC,\s\up7(―→)) B.eq \f(4,3)eq \(AB,\s\up7(―→))－eq \f(5,6)eq \(AC,\s\up7(―→))
C.eq \f(5,6)eq \(AB,\s\up7(―→))＋eq \f(4,3)eq \(AC,\s\up7(―→)) D.eq \f(4,3)eq \(AB,\s\up7(―→))＋eq \f(5,6)eq \(AC,\s\up7(―→))
解析：选A ∵D为AB的中点，点E满足eq \(EB,\s\up7(―→))＝4eq \(EC,\s\up7(―→))，
∴eq \(BD,\s\up7(―→))＝eq \f(1,2)eq \(BA,\s\up7(―→))，eq \(EB,\s\up7(―→))＝eq \f(4,3)eq \(CB,\s\up7(―→))，
∴eq \(ED,\s\up7(―→))＝eq \(EB,\s\up7(―→))＋eq \(BD,\s\up7(―→))＝eq \f(4,3)eq \(CB,\s\up7(―→))－eq \f(1,2)eq \(AB,\s\up7(―→))
＝eq \f(4,3)eq \b\lc\(\rc\)(\a\vs4\al\c1(eq \(AB,\s\up7(―→))－eq \(AC,\s\up7(―→)) ))－eq \f(1,2)eq \(AB,\s\up7(―→))＝eq \f(5,6)eq \(AB,\s\up7(―→))－eq \f(4,3)eq \(AC,\s\up7(―→)).
2．设M是△ABC所在平面上的一点，eq \(MB,\s\up7(―→))＋eq \f(3,2)eq \(MA,\s\up7(―→))＋eq \f(3,2)eq \(MC,\s\up7(―→))＝0，D是AC的中点，teq \(MB,\s\up7(―→))＝eq \(DM,\s\up7(―→))，则实数t的值为( )
A．eq \f(1,2) B．eq \f(1,3) C．2 D．1
解析：选B 因为D是AC的中点，所以eq \(MA,\s\up7(―→))＋eq \(MC,\s\up7(―→))＝2eq \(MD,\s\up7(―→))，又因为eq \(MB,\s\up7(―→))＋eq \f(3,2)eq \(MA,\s\up7(―→))＋eq \f(3,2)eq \(MC,\s\up7(―→))＝0，所以eq \f(1,3)eq \(MB,\s\up7(―→))＋eq \f(1,2)(eq \(MA,\s\up7(―→))＋eq \(MC,\s\up7(―→)))＝eq \f(1,3)eq \(MB,\s\up7(―→))＋eq \(MD,\s\up7(―→))＝0，即eq \f(1,3)eq \(MB,\s\up7(―→))＝eq \(DM,\s\up7(―→))，又因为teq \(MB,\s\up7(―→))＝eq \(DM,\s\up7(―→))，所以t＝eq \f(1,3).
3．在正六边形ABCDEF中，对角线BD，CF相交于点P，若eq \(AP,\s\up7(―→))＝xeq \(AB,\s\up7(―→))＋yeq \(AF,\s\up7(―→))，则x＋y＝________.
解析：如图，记正六边形ABCDEF的中心为点O，连接OB，OD，易证四边形OBCD为菱形且P恰为其中心．
∴eq \(FP,\s\up7(―→))＝eq \f(3,2)eq \(FO,\s\up7(―→))＝eq \f(3,2)eq \(AB,\s\up7(―→))，∴eq \(AP,\s\up7(―→))＝eq \(AF,\s\up7(―→))＋eq \(FP,\s\up7(―→))＝eq \(AF,\s\up7(―→))＋eq \f(3,2)eq \(AB,\s\up7(―→))，∵eq \(AP,\s\up7(―→))＝xeq \(AB,\s\up7(―→))＋yeq \(AF,\s\up7(―→))，∴x＝eq \f(3,2)，y＝1，∴x＋y＝eq \f(5,2).
答案：eq \f(5,2)
命题视角三 共线向量定理的应用
[典例] (1)已知a，b是不共线的向量，eq \(AB,\s\up7(―→))＝λa＋b，eq \(AC,\s\up7(―→))＝a＋μb(λ，μ∈R)，若A，B，C三点共线，则λ，μ的关系一定成立的是( )
A．λμ＝1 B．λμ＝－1
C．λ－μ＝－1 D．λ＋μ＝2
(2)设e1与e2是两个不共线向量，eq \(AB,\s\up7(―→))＝3e1＋2e2，eq \(CB,\s\up7(―→))＝ke1＋e2，eq \(CD,\s\up7(―→))＝3e1－2ke2，若A，B，D三点共线，则k的值为________．
[解析] (1)∵eq \(AB,\s\up7(―→))与eq \(AC,\s\up7(―→))有公共点A，∴若A，B，C三点共线，则存在一个实数t使eq \(AB,\s\up7(―→))＝teq \(AC,\s\up7(―→))，即λa＋b＝ta＋μtb，则eq \b\lc\{\rc\ (\a\vs4\al\c1(λ＝t，,μt＝1，))消去参数t得λμ＝1；反之，当λμ＝1时，eq \(AB,\s\up7(―→))＝eq \f(1,μ)a＋b，此时存在实数eq \f(1,μ)使eq \(AB,\s\up7(―→))＝eq \f(1,μ)eq \(AC,\s\up7(―→))，故eq \(AB,\s\up7(―→))和eq \(AC,\s\up7(―→))共线．∵eq \(AB,\s\up7(―→))与eq \(AC,\s\up7(―→))有公共点A，∴A，B，C三点共线．故选A.
(2)由题意，A，B，D三点共线，故必存在一个实数λ，使得eq \(AB,\s\up7(―→))＝λeq \(BD,\s\up7(―→)).又eq \(AB,\s\up7(―→))＝3e1＋2e2，eq \(CB,\s\up7(―→))＝ke1＋e2，eq \(CD,\s\up7(―→))＝3e1－2ke2，所以eq \(BD,\s\up7(―→))＝eq \(CD,\s\up7(―→))－eq \(CB,\s\up7(―→))＝3e1－2ke2－(ke1＋e2)＝(3－k)e1－(2k＋1)e2，所以3e1＋2e2＝λ(3－k)e1－λ(2k＋1)e2，又e1与e2不共线，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(3＝λ3－k，,2＝－λ2k＋1，))解得k＝－eq \f(9,4).
[答案] (1)A (2)－eq \f(9,4)
[方法技巧] 平面向量共线定理的3个应用
[针对训练]
1．已知两个非零向量a，b互相垂直，若向量m＝4a＋5b与n＝2a＋λb共线，则实数λ的值为( )
A．5 B．3 C.eq \f(5,2) D．2
解析：选C ∵a，b是非零向量，且互相垂直，
∴4a＋5b≠0，m≠0.
∵m，n共线，∴n＝μm，即2a＋λb＝μ(4a＋5b)，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(2＝4μ，,λ＝5μ.))解得λ＝eq \f(5,2).
2．在△ABC中，E，F分别为AC，AB上的点，BE与CF交于点Q，且eq \(AE,\s\up7(―→))＝2eq \(EC,\s\up7(―→))，eq \(AF,\s\up7(―→))＝3eq \(FB,\s\up7(―→))，AQ交BC于点D，eq \(AQ,\s\up7(―→))＝λeq \(QD,\s\up7(―→))，则λ的值为( )
A．3 B．4 C．5 D．6
解析：选C 因为B，Q，E三点共线，所以可设eq \(AQ,\s\up7(―→))＝xeq \(AB,\s\up7(―→))＋(1－x)eq \(AE,\s\up7(―→))＝xeq \(AB,\s\up7(―→))＋eq \f(2,3)(1－x)eq \(AC,\s\up7(―→)).因为C，Q，F三点共线，所以可设eq \(AQ,\s\up7(―→))＝yeq \(AC,\s\up7(―→))＋(1－y)eq \(AF,\s\up7(―→))＝yeq \(AC,\s\up7(―→))＋eq \f(3,4)(1－y)eq \(AB,\s\up7(―→))，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝\f(3,4)1－y，,y＝\f(2,3)1－x，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝\f(1,2)，,y＝\f(1,3).))所以eq \(AQ,\s\up7(―→))＝eq \f(1,2)eq \(AB,\s\up7(―→))＋eq \f(1,3)eq \(AC,\s\up7(―→))＝eq \f(λ,1＋λ)eq \(AD,\s\up7(―→))，所以eq \(AD,\s\up7(―→))＝eq \f(1＋λ,2λ) eq \(AB,\s\up7(―→))＋eq \f(1＋λ,3λ)eq \(AC,\s\up7(―→)).因为B，D，C三点共线，所以eq \f(1＋λ,2λ)＋eq \f(1＋λ,3λ)＝1，解得λ＝5.
3．已知O为△ABC内一点，且2eq \(AO,\s\up7(―→))＝eq \(OB,\s\up7(―→))＋eq \(OC,\s\up7(―→))，eq \(AD,\s\up7(―→))＝teq \(AC,\s\up7(―→))，若B，O，D三点共线，则t的值为________．
解析：设线段BC的中点为M，则eq \(OB,\s\up7(―→))＋eq \(OC,\s\up7(―→))＝2eq \(OM,\s\up7(―→)).
因为2eq \(AO,\s\up7(―→))＝eq \(OB,\s\up7(―→))＋eq \(OC,\s\up7(―→))，所以eq \(AO,\s\up7(―→))＝eq \(OM,\s\up7(―→))，
则eq \(AO,\s\up7(―→))＝eq \f(1,2)eq \(AM,\s\up7(―→))＝eq \f(1,4)(eq \(AB,\s\up7(―→))＋eq \(AC,\s\up7(―→)))＝eq \f(1,4)eq \b\lc\(\rc\)(\a\vs4\al\c1(eq \(AB,\s\up7(―→))＋\f(1,t) eq \(AD,\s\up7(―→)) ))＝eq \f(1,4)eq \(AB,\s\up7(―→))＋eq \f(1,4t)eq \(AD,\s\up7(―→)).
由B，O，D三点共线，得eq \f(1,4)＋eq \f(1,4t)＝1，解得t＝eq \f(1,3).
答案：eq \f(1,3)
巧用性质·练转化思维——三点共线定理的妙用
已知O，A，B是不共线的三点，且eq \(OP,\s\up7(―→))＝meq \(OA,\s\up7(―→))＋neq \(OB,\s\up7(―→))(m，n∈R)，则A，P，B三点共线的充要条件是m＋n＝1.
1．(求参数值)如图，在△ABC中，eq \(AN,\s\up7(―→))＝eq \f(1,3)eq \(AC,\s\up7(―→))，P是BN上的一点，若eq \(AP,\s\up7(―→))＝meq \(AB,\s\up7(―→))＋eq \f(2,11)eq \(AC,\s\up7(―→))，则实数m的值为( )
A.eq \f(9,11) B.eq \f(5,11)
C.eq \f(3,11) D.eq \f(2,11)
解析：选B 注意到N，P，B三点共线，
因此eq \(AP,\s\up7(―→))＝meq \(AB,\s\up7(―→))＋eq \f(2,11)eq \(AC,\s\up7(―→))＝meq \(AB,\s\up7(―→))＋eq \f(6,11)eq \(AN,\s\up7(―→))，
从而m＋eq \f(6,11)＝1，所以m＝eq \f(5,11).
2．(求参数范围)在△ABC中，点D是线段BC(不包括端点)上的动点．若eq \(AB,\s\up7(―→))＝xeq \(AC,\s\up7(―→))＋yeq \(AD,\s\up7(―→))，则( )
A．x>1B．y>1 C．x＋y>1D．xy>1
解析：选B 设eq \(BD,\s\up7(―→))＝λeq \(BC,\s\up7(―→)) (0