人教版九下数学期末检测卷03（冲刺满分）（解析版）

这是一份人教版九下数学期末检测卷03（冲刺满分）（解析版），共19页。试卷主要包含了相反数的是，下列各式是最简二次根式的是，下列图形中，是中心对称图形的是等内容，欢迎下载使用。

1．相反数的是（ ）
A．B．C．D．
【答案】D
【详解】解：∵和为零的两个数称作互为相反数
∴的相反数是.
故选D.
2．2022年3月11日，新华社发文总结2021年中国取得的科技成就．其中包括：中国高铁运营里程超40000000米，将数40000000用科学计数法表示为（ ）
A．B．C．D．
【答案】D
【详解】解：40000000用科学计数法表示为，
故选：D．
3．下列各式是最简二次根式的是（ ）
A．B．C．D．
【答案】C
【详解】解：A、，不是最简二次根式，故本选项不符合题意；
B、，不是最简二次根式，故本选项不符合题意；
C、是最简二次根式，故本选项符合题意；
D、，不是最简二次根式，故本选项不符合题意；
故选：C
4．下列图形中，是中心对称图形的是（ ）
A．B．C．D．
【答案】B
【详解】解：A、是轴对称图形，不是中心对称图形，不符合题意；
B、是中心对称图形，符合题意；
C、是轴对称图形，不是中心对称图形，不符合题意；
D、既不是轴对称图形，也是中心对称图形，不符合题意；
故选：B．
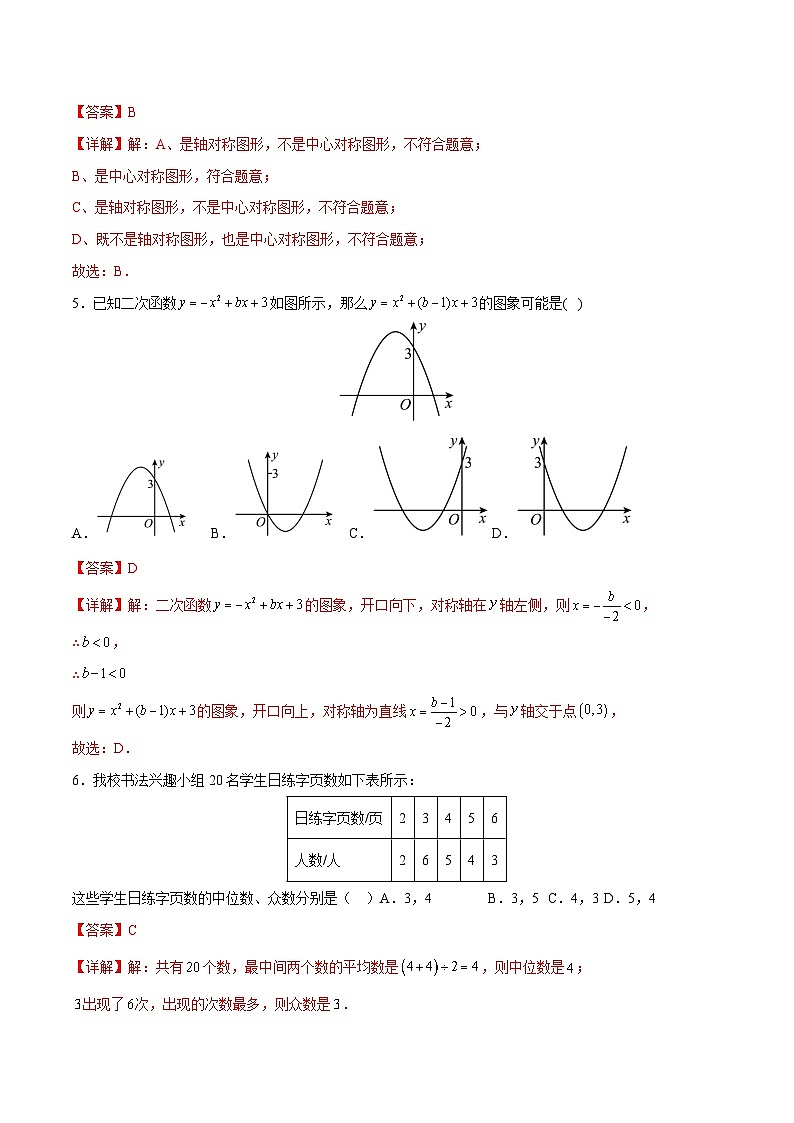
5．已知二次函数如图所示，那么的图象可能是( )
A．B．C．D．
【答案】D
【详解】解：二次函数的图象，开口向下，对称轴在轴左侧，则，
∴，
∴
则的图象，开口向上，对称轴为直线，与轴交于点，
故选：D．
6．我校书法兴趣小组20名学生日练字页数如下表所示：
这些学生日练字页数的中位数、众数分别是（ ）A．3，4B．3，5C．4，3D．5，4
【答案】C
【详解】解：共有个数，最中间两个数的平均数是，则中位数是；
出现了次，出现的次数最多，则众数是．
故选：C．
7．一个不透明的袋子中装有18个小球，其中12个红球、6个绿球，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球．则摸出的小球是红球的概率是（ ）
A．B．C．D．
【答案】A
【详解】解：∵一个不透明的袋子中装有18个小球，其中12个红球、6个绿球，
∴从袋子中随机摸出一个小球，则摸出的小球是红球的概率为．
故选：A．
8．观察下列图形及图形所对应的算式，根据你发现的规律计算（n是正整数）的结果为（ ）
A．B．C．D．
【答案】A
【详解】解：图（1）：；
图（2）： ；
图（3）：；
…；
那么图（n）：．
故选：A．
9．如图，已知的面积为10，平分，且于点，则的面积是（ ）
A．10B．8C．5D．4
【答案】C
【详解】解：延长交于，
平分，
，
，
，
在和中，
，
，
，
，，
，
故选：C．
10．如图，点，，在同一直线上，和均是等边三角形，与交于点，，分别与，交于点，，有如下结论：；②；③；④；⑤．其中正确的结论有：（ ）
A．5个B．4个C．3个D．2个
【答案】A
【详解】解：和均是等边三角形，
，，，
，即．
在和中，
，
，
，，故①正确．
，
．
在和中，
，
，故②正确，
，，
，即，故③正确．
，，
是等边三角形，
，
，
，故④正确．
，
．
中，，
．
，
，故⑤正确．
综上所述，正确的结论有①②③④⑤，共5个．
故答案为：A．
填空题（本大题共4小题，每小题5分，满分20分）
11．已知，，且，则________．
【答案】或##或
【详解】解：∵，，
∴，
∵，
∴，即，
∴，
当时，，
当当时，，
综上所述，或
故答案为：或．
12．若抛物线与轴没有交点，则的取值范围为______．
【答案】
【详解】解：抛物线与轴没有交点，
一元二次方程没有实数根，
，
．
故答案为：．
13．如图等边内接于⊙O，若⊙O的半径为1，以阴影部分为侧面围成一个圆锥，从剩余部分剪出一个圆作为圆锥底面，则圆锥的全面积为______．
【答案】##
【详解】解：∵是等边三角形，
∴．
∴，
∴，，
设圆锥的底面半径为r，
则，
∴，
∴圆锥的底面积，
∴圆锥的全面积．
故答案为：．
14．如图，点为双曲线在第二象限上的动点，的延长线与双曲线的另一个交点为，以为边的矩形满足，对角线，交于点，设的坐标为，则，满足的关系式为______．
【答案】
【详解】解：连接，分别过点、作轴的垂线，垂足为、，
，
四边形是矩形，
，，
，
，，
，，
，
，
，
，
，
，
点为双曲线 在第二象限上的动点，
设点的坐标为，
，
，
的坐标为，
，
，
故答案为：．
三、解答题（本大题共9小题，满分90分）
15．（6分）计算：．
【答案】
【详解】解：
16．（8分）解方程组：
(1)；
(2)．
【答案】(1)
(2)
【详解】（1）解：，
由②得③，
把③代入①得，，
解得，，
把代入③得，
所以方程组的解为；
（2），
①得，③，
③②得，，
解得，，
把，代入②得，，
解得，，
所以方程组的解．
17．（8分）如图，在四边形中，，是对角线，是等边三角形．线段绕点顺时针旋转得到线段，连接，．
(1)求证：；
(2)若，，，求的长．
【答案】(1)见解析
(2)8
【详解】（1）证明：由旋转可知，，
∵是等边三角形，
∴，，
∴，
∴，即；
（2）解：在和中，
∵，
∴，
∴，
∵，，
∴是等边三角形，
∴，
又∵，
∴，
在中，．
18．（10分）为了更好地贯彻落实国家关于“强化体育课和课外锻炼，促进青少年身心健康、体魄强健”的精神，某校大力开展体育活动．该校抽查了部分同学对于足球、篮球、乒乓球、跳绳四个体育活动的参与情况．经调查，人数分布情况的扇形图和条形图如下：
(1)该班学生有 人，跳绳人数所占扇形圆心角的度数 ．
(2)请你补全条形图；
(3)若该校有人，估计该校参与足球活动的学生有多少人？．
【答案】(1)，
(2)见解析
(3)人
【详解】（1）解：由扇形图可知，乒乓球小组人数占全班人数的．
由条形图可知，乒乓球小组人数为．故全班人数为．
篮球人数为：人，则跳绳的人数为：（人）
因为跳绳小组人数占全班人数的，
所以，它所占扇形圆心角的大小为．
故答案为：，．
（2）补全条形统计图如图．
（3）（人）
答：估计该校参与足球活动的学生有人
19．（10分）时隔多日，为“弘扬雷锋精神，传承红色基因”我校开展了志愿者服务活动，2020级初三年段的6位历史老师们又扛起了这一大梁，他们自告奋勇，打算从1位女老师和5位男老师中随机选取若干位担任志愿者．
(1)若只需选择一位担任志愿者，恰好选中这位女老师的概率是 ；
(2)这5位男老师分别记为，，，，，其中，，三位老师是班主任．若要从这5位男老师中随机抽取两位担任志愿者，请用列表法或画树状图的方法求抽到的两位都是班主任的概率．
【答案】(1)
(2)．
【详解】（1）解：从1位女老师和5位男老师中随机选取若干位担任志愿者，
若只需选择一位担任志愿者，恰好选中这位女老师的概率是；
故答案为：；
（2）解：画出树状图为：
共有20种等可能的结果数，其中抽取的两个老师恰好都是班主任的结果数为6，
所以抽取的两个老师恰好都是班主任的概率．
20．（10分）甲、乙两支工程队修建公路，已知甲队每天修路的长度是乙队的2倍，如果两队各自修建公路600米，甲队比乙队少用5天．
(1)求甲、乙两支工程队每天各修路多少米？
(2)现在需要修建一段长4800米的公路，因工程需要，需由甲、乙两支工程队施工完成．若甲队每天所需费用为1.2万元，乙队每天所需费用为0.5万元，求在总费用不超过45万元的情况下，至少安排乙队施工多少天？
【答案】(1)甲队每天修120米，乙队每天修60米
(2)30
【详解】（1）解：设乙队每天修x米，则甲队每天修2x米，根据题意列方程
解得：；
经检验，是原方程的解；
，
答：甲队每天修120米，乙队每天修60米．
（2）解：设安排乙队施工m天，则甲队需施工天．
依题意可得：
∴，
解得：；
答：至少安排乙队施工30天．
21．（12分）四边形内接于，为的中点，交于点，于点．已知，．
(1)求弦的长．
(2)若，求四边形的面积．
【答案】(1)8
(2)
【详解】（1）解：连接，如图所示：
，，
，
为的中点，
，，
，
，
；
（2）解：作直径，连接，如图所示：
，
，
，
，
，
，
，
是的直径，
，
，
，
，
，由勾股定理得：，
．
22．（12分）我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”(如图所示)就是一例．这个三角形的构造法则为：两腰上的数都是1，其余每个数均为其上方（左右）两数之和．事实上，这个三角形给出了(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律．例如，在三角形中第行的三个数1，2，1，恰好对应展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应展开式中各项的系数等等．
（1）请写出的展开式= ；
（2）根据规律计算：；
（3）若（2x﹣1）2018＝a1x2018+a2x2017+a3x2016+……+a2017x2+a2018x+a2019，求a1+a2+a3+……+a2017+a2018的值．
【答案】(1) ，（2）-1，（3）1
【详解】解:(1)根据题意得：（a+b）5的展开式中各项系数分别为1，5，10，10，5，1，
∴，
故答案为：；
(2)；
(3) 当x＝0时，a2019＝1，
当x＝1时，a1+a2+a3+…+a2017+a2018+a2019＝1，
∴a1+a2+a3+…+a2017+a2018＝0．
23．（14分）已知如图，直线与两坐标轴分别交于点、，点关于轴的对称点是点，直线经过点，且与轴相交于点，点是直线上一动点，过点作轴的平行线交直线于点，再以为边向右边作正方形．
(1)①求的值；
②判断的形状，并说明理由；
(2)连接、，当的周长最短时，求点的坐标；
(3)在（2）的条件下，在轴上是否存在一点，使得是等腰三角形，若存在，请直接写出点的坐标，若不存在，请说明理由．
【答案】(1)①②等边三角形，理由见解析
(2)
(3)在轴上存在一点，使得是等腰三角形，点坐标为或或或
【详解】（1）解：①令，则，
，
直线经过点，
；
②是等边三角形，理由如下：
令，则，
解得，
，
点关于轴的对称点是点，
，
，，，
是等边三角形；
（2）解：，
直线，
令，则，
，
设点关于直线的对称点为，
，
，
，
，
，
连接，则与直线的交点为点，
，
的周长，
当、、三点共线时，的周长最小，
设直线的解析式为，
，
解得，
，
联立方程组，
解得，
，
轴，
，
，
四边形是正方形，
；
（3）解：在轴上存在一点，使得是等腰三角形，理由如下：
设，
，，，
当时，，
解得或，
或；
当时，，
解得，
；
当时，，
解得或舍，
；
综上所述：点坐标为或或或．
日练字页数/页
2
3
4
5
6
人数/人
2
6
5
4
3