初中数学苏科版（2024）八年级上册1.3 探索三角形全等的条件图文课件ppt

这是一份初中数学苏科版（2024）八年级上册1.3 探索三角形全等的条件图文课件ppt，共39页。PPT课件主要包含了书写格式等内容，欢迎下载使用。
第4课时 利用斜边和直角边判定直角三角形全等
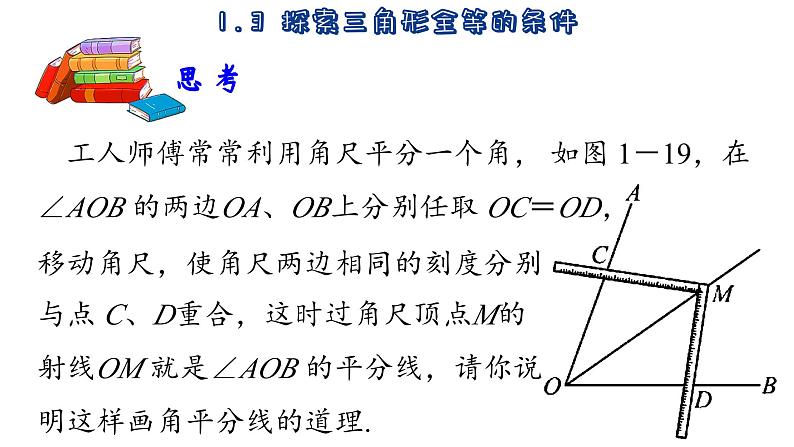
工人师傅常常利用角尺平分一个角， 如图 1－19，在∠AOB 的两边OA、OB上分别任取 OC＝OD，移动角尺，使角尺两边相同的刻度分别与点 C、D重合，这时过角尺顶点M的射线OM 就是∠AOB 的平分线，请你说明这样画角平分线的道理.
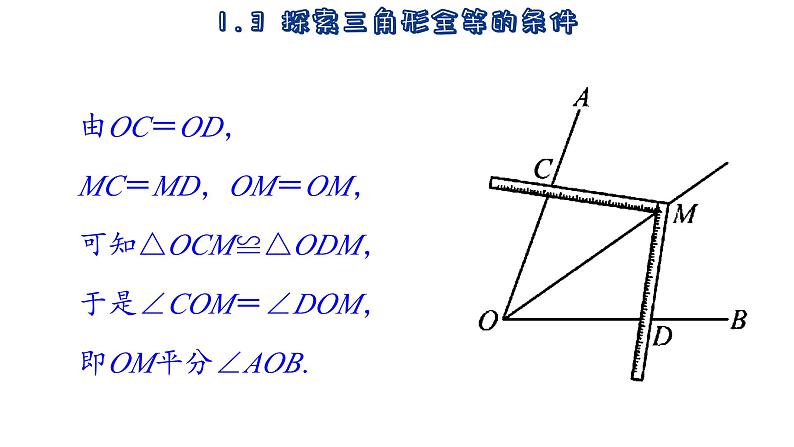
由OC＝OD， MC＝MD，OM＝OM，可知△OCM≌△ODM，于是∠COM＝∠DOM，即OM平分∠AOB.
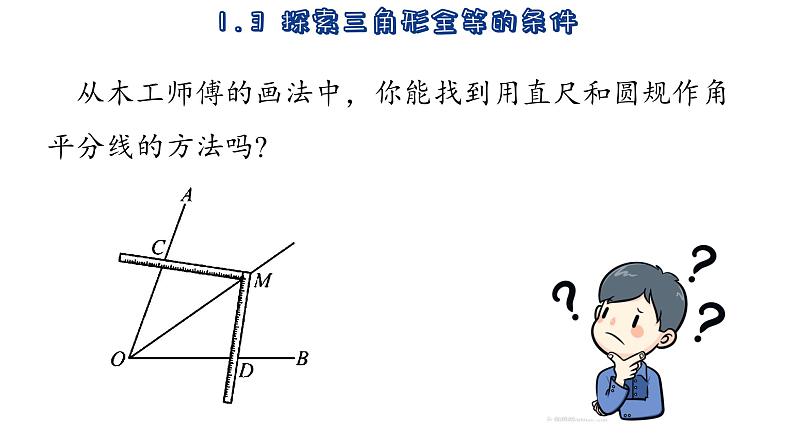
从木工师傅的画法中，你能找到用直尺和圆规作角平分线的方法吗?
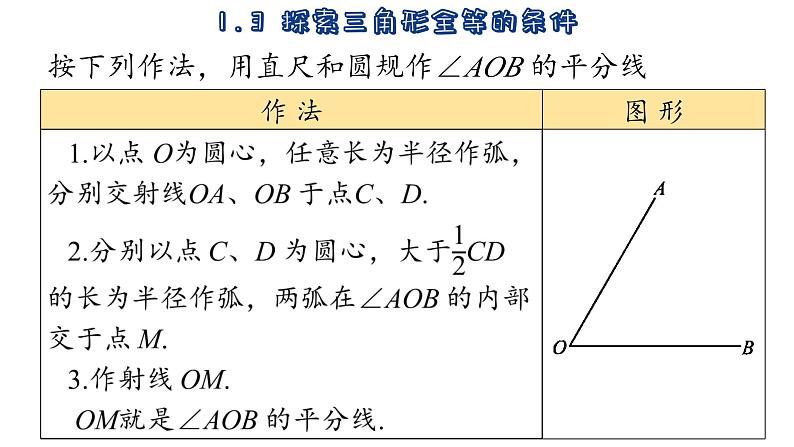
按下列作法，用直尺和圆规作∠AOB 的平分线
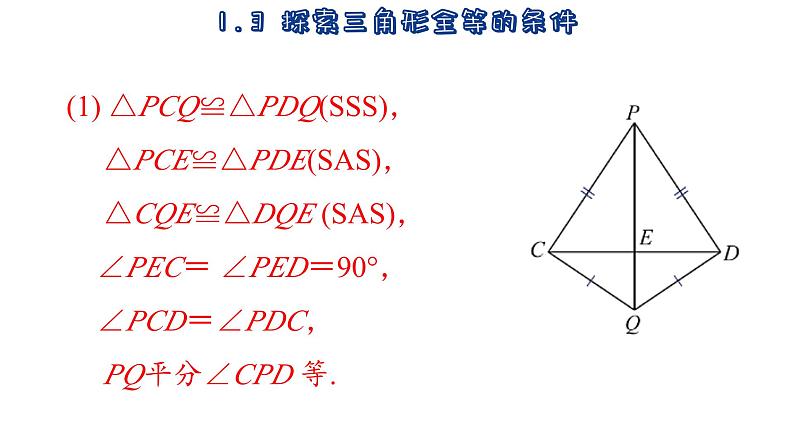
如图1－20，PC＝PD，QC＝QD，PQ、CD 相交于点 E. (1) 根据以上条件，你能发现哪些结论?
(1) △PCQ≌△PDQ(SSS)， △PCE≌△PDE(SAS)， △CQE≌△DQE (SAS)， ∠PEC＝ ∠PED＝90°， ∠PCD＝∠PDC， PQ平分∠CPD 等.
(2) 你能证明 PQ⊥CD 吗?由此，你能找到用直尺和圆规过已知直线外一点作这条直线的垂线的方法吗?
按下列作法，用直尺和圆规经过直线 AB 外一点 P 作 AB 的垂线.
如果点 P在直线AB 上，如何用直尺和圆规经过点 P作AB 的垂线?
作法： (1)以点 P 为圆心,适当的长为半径作弧，使它与AB 交于点C，D.
1. (1)用直尺和圆规把图①中的∠MON 四等分；
解：作法：如图所示， ①作∠MON 的平分线OA. ②作∠MOA 的平分线OB. ③作∠NOA 的平分线OC.则 OA，OB，OC 四等分∠MON.
(2) 用直尺和圆规在图②中过点 B作 BC 的垂线，并指出所作图中∠ABC的余角.
① 如图所示，反向延长射线 BC，以点 B 为圆心，以适当长为半径作弧交直线 BC 于点 D，E.
2. 用直尺和圆规作一个直角三角形，使它的两条直角边分别等于 a、b.
解：作法：如图所示， (1) 作线段 AB＝b. (2) 延长线段 BA，过点A作AD⊥AB. (3) 在射线AD上截取AC＝a，连接 BC. Rt△ABC 即为所求作的三角形.
两个直角三角形，有一对内角(直角)相等，判定两个直角三角形全等，还需要几个条件?可以是哪些条件?
直角三角形是特殊的三角形，可以用符号“Rt△”表示. 判定两个直角三角形全等，有没有特殊的方法?
这两个直角三角形全等吗?
按下列作法，用直尺和圆规作 Rt△ABC，使 ∠C＝90°，CB＝a，AB＝c.
你作的直角三角形与其他同学作的直角三角形能完全重合吗?
如图，在△ABC和△A′B′C′中，∠C＝∠C′＝90°，AB＝A′B′，AC＝A′C′，怎样证明 △ABC≌△A′B′C′?
把两个直角三角形拼在一起 像本节例7那样，可以证得 ∠B＝∠B′.
在△ABC和△A′B′C′中，由∠B＝∠B′，∠ACB＝∠A′C′B′，AB＝A′B′，可以证明△ABC≌△A′B′C′ (AAS).
于是，我们得到如下定理：
斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
如图，在Rt△ABC 和Rt△A′B′C′中， AB＝A′B′， BC＝B′C′， ∴ Rt△ABC ≌ Rt△A′B′C′(HL).
例8 已知：如图1－22，AD、BC 相交于点O，AD＝BC. ∠C＝∠D ＝ 90°. 求证：AO＝BO，CO＝DO.
分析：要证 AO＝BO、CO＝DO，只要证△AOC≌△BOD. 由于∠C＝∠D＝90°，∠AOC＝∠BOD，于是只要证 AC＝BD，所以就要证 △ABC ≌△BAD.
已知：如图，AC⊥BC，AD⊥BD，垂足分别是点C、D，AD＝BC，CE⊥ AB，DF⊥ AB，垂足分别是点E、F. 求证：CE＝DF.
1. 如图，方格纸中有点 A、B、C、D、E、F，以其中的3个点为顶点，画出所有的直角三角形，并找出其中全等的直角三角形.
解：画直角三角形如图所示，全等的直角三角形有：△ABC≌△BDE≌△BFE≌△BFC≌△CEB≌△CEF；△ABF≌△DBF；△DCF≌△AEF.
2. 如图，AC⊥CB，AD⊥DB，要证明△ABC≌△ABD，还需要什么条件?
解：∠CAB＝∠DAB 或∠ABC＝∠ABD 或 BC＝BD或AC＝AD. (答案不唯一)
3. 已知：如图，AD＝BC，CA⊥AB，AC⊥CD. 求证：AD∥BC.
证明：∵CA⊥AB，AC⊥CD (已知)， ∴∠BAC＝∠DCA ＝ 90° (垂直的定义).
利用斜边和直角边判定直角三角形全等
判定直角三角形全等的“四种思路”：(1) 若已知条件中有一组直角边和一组斜边分别相等， 用“HL”判定．(2) 若有一组锐角和斜边分别相等，用“AAS”判定．