广东版高考物理复习专题一0一磁场练习课件

这是一份广东版高考物理复习专题一0一磁场练习课件，共59页。

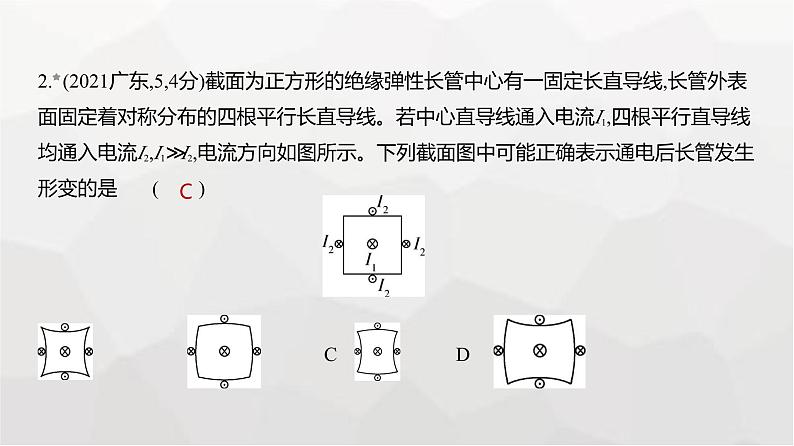
2. (2021广东,5,4分)截面为正方形的绝缘弹性长管中心有一固定长直导线,长管外表面固定着对称分布的四根平行长直导线。若中心直导线通入电流I1,四根平行直导线 均通入电流I2,I1≫I2,电流方向如图所示。下列截面图中可能正确表示通电后长管发生 形变的是     (　    )  A　　　     B　　　     C　　　     D
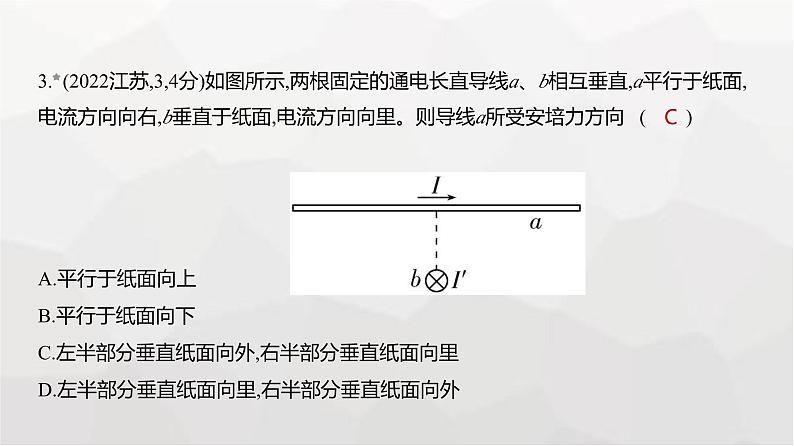
3. (2022江苏,3,4分)如图所示,两根固定的通电长直导线a、b相互垂直,a平行于纸面,电流方向向右,b垂直于纸面,电流方向向里。则导线a所受安培力方向 (　    ) A.平行于纸面向上B.平行于纸面向下C.左半部分垂直纸面向外,右半部分垂直纸面向里D.左半部分垂直纸面向里,右半部分垂直纸面向外
5. (2022湖南,3,4分)如图(a),直导线MN被两等长且平行的绝缘轻绳悬挂于水平轴OO'上,其所在区域存在方向垂直指向OO'的磁场,与OO'距离相等位置的磁感应强度大小 相等且不随时间变化,其截面图如图(b)所示。导线通以电流I,静止后,悬绳偏离竖直方 向的夹角为θ。下列说法正确的是 (　    ) 
A.当导线静止在图(a)右侧位置时,导线中电流方向由N指向MB.电流I增大,静止后,导线对悬绳的拉力不变C.tan θ与电流I成正比D.sin θ与电流I成正比
考点二　磁场对运动电荷的作用
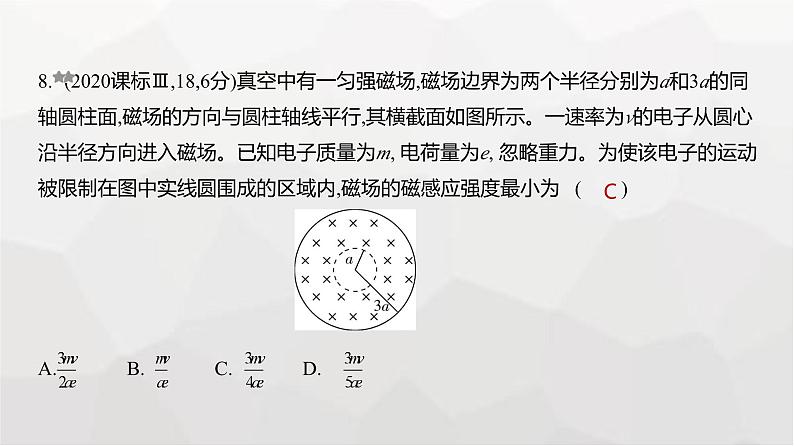
8. (2020课标Ⅲ,18,6分)真空中有一匀强磁场,磁场边界为两个半径分别为a和3a的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图所示。一速率为v的电子从圆心 沿半径方向进入磁场。已知电子质量为m, 电荷量为e, 忽略重力。为使该电子的运动 被限制在图中实线圆围成的区域内,磁场的磁感应强度最小为 (　    ) A. 　     B. 　     C. 　     D. 
10. (2020课标Ⅱ,24,12分)如图,在0≤x≤h,-∞0)的粒 子以速度v0从磁场区域左侧沿x轴进入磁场,不计重力。(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,分析说明磁场的方向,并求在这种情 况下磁感应强度的最小值Bm;(2)如果磁感应强度大小为 ,粒子将通过虚线所示边界上的一点离开磁场。求粒子在该点的运动方向与x轴正方向的夹角及该点到x轴的距离。
答案    (1)由题意,粒子刚进入磁场时应受到方向向上的洛伦兹力,因此磁场方向垂直 于纸面向里。设粒子进入磁场中做圆周运动的半径为R,根据洛伦兹力公式和圆周运 动规律,有qv0B=m  ①由此可得R=  ②粒子穿过y轴正半轴离开磁场,其在磁场中做圆周运动的圆心在y轴正半轴上,半径应满 足R≤h ③
由题意,当磁感应强度大小为Bm时,粒子的运动半径最大,由此得Bm= 。 ④(2)若磁感应强度大小为 ,粒子做圆周运动的圆心仍在y轴正半轴上,结合②④式可得,此时圆弧半径为R'=2h ⑤粒子会穿过图中P点离开磁场,运动轨迹如图所示。 
设粒子在P点的运动方向与x轴正方向的夹角为α,由几何关系有sin α= =  ⑥得α=  ⑦由几何关系可得,P点到x轴的距离为y=2h(1-cs α) ⑧联立⑦⑧式得y=(2- )h。 ⑨
11. (2019课标Ⅰ,24,12分)如图,在直角三角形OPN区域内存在匀强磁场,磁感应强度大小为B、方向垂直于纸面向外。一带正电的粒子从静止开始经电压U加速后,沿 平行于x轴的方向射入磁场;一段时间后,该粒子在OP边上某点以垂直于x轴的方向射 出。已知O点为坐标原点,N点在y轴上,OP与x轴的夹角为30°,粒子进入磁场的入射点 与离开磁场的出射点之间的距离为d,不计重力。求(1)带电粒子的比荷;(2)带电粒子从射入磁场到运动至x轴的时间。
模型一　带电粒子在叠加场中的运动
1. (2023海南,2,3分)如图所示,带正电的小球竖直向下射入垂直纸面向里的匀强磁场,关于小球运动和受力的说法正确的是 (　    )A.小球刚进入磁场时受到的洛伦兹力水平向右B.小球运动过程中的速度不变C.小球运动过程中的加速度保持不变D.小球受到的洛伦兹力对小球做正功
3. (2022全国甲,18,6分)空间存在着匀强磁场和匀强电场,磁场的方向垂直于纸面(xOy平面)向里,电场的方向沿y轴正方向。一带正电的粒子在电场和磁场的作用下,从 坐标原点O由静止开始运动。下列四幅图中,可能正确描述该粒子运动轨迹的是 (        ) 
7. (2023江苏,16,15分)霍尔推进器某局部区域可抽象成如图所示的模型。Oxy平面内存在竖直向下的匀强电场和垂直坐标平面向里的匀强磁场,磁感应强度为B。质量为 m、电荷量为e的电子从O点沿x轴正方向水平入射。入射速度为v0时,电子沿x轴做直 线运动;入射速度小于v0时,电子的运动轨迹如图中的虚线所示,且在最高点与在最低点 所受的合力大小相等。不计重力及电子间相互作用。(1)求电场强度的大小E;(2)若电子入射速度为 ,求运动到速度为 时位置的纵坐标y1;(3)若电子入射速度在0模型二　带电粒子在组合场中的运动
9. (2022广东,7,4分)如图所示,一个立方体空间被对角平面MNPQ划分成两个区域,两区域分布有磁感应强度大小相等、方向相反且与z轴平行的匀强磁场。一质子 以某一速度从立方体左侧垂直Oyz平面进入磁场,并穿过两个磁场区域。下列关于质 子运动轨迹在不同坐标平面的投影中,可能正确的是 (　    ) 
10. (2019课标Ⅲ,18,6分)如图,在坐标系的第一和第二象限内存在磁感应强度大小分别为 B和B、方向均垂直于纸面向外的匀强磁场。一质量为m、电荷量为q(q>0)的粒子垂直于x轴射入第二象限,随后垂直于y轴进入第一象限,最后经过x轴离开第一象 限。粒子在磁场中运动的时间为 (　    ) A. 　    B. 　    C. 　    D. 
12. (2023辽宁,14,13分)如图,水平放置的两平行金属板间存在匀强电场,板长是板间距离的 倍。金属板外有一圆心为O的圆形区域,其内部存在磁感应强度大小为B、方向垂直于纸面向外的匀强磁场。质量为m、电荷量为q(q>0)的粒子沿中线以速度v0 水平向右射入两板间,恰好从下板边缘P点飞出电场,并沿PO方向从图中O'点射入磁 场。已知圆形磁场区域半径为 ,不计粒子重力。(1)求金属板间电势差U。(2)求粒子射出磁场时与射入磁场时运动方向间的夹角θ。(3)仅改变圆形磁场区域的位置,使粒子仍从图中O'点射入磁场,且在磁场中的运动时 间最长。定性画出粒子在磁场中的运动轨迹及相应的弦,标出改变后的圆形磁场区域的圆心M。
答案    (1)     (2)60°或     (3)粒子在圆形磁场区域中的运动轨迹对应的弦越长,运动时间越长,故运动轨迹对应的弦为圆形磁场区域的直径时,粒子在磁场中的运动时
间最长,设粒子射入磁场时的速度方向与水平方向夹角为β,则有cs β= = ,即β=30°,如图2所示,由几何关系知cs α= = ,故30°<α<60°,故可找到弦O'A的位置(其中A为粒子射出圆形磁场区域的位置)、圆心M的位置,进而画出粒子的运动轨迹。
13. (2021广东,14,15分)如图是一种花瓣形电子加速器简化示意图。空间有三个同心圆a、b、c围成的区域,圆a内为无场区,圆a与圆b之间存在辐射状电场,圆b与圆c之间 有三个圆心角均略小于90°的扇环形匀强磁场区Ⅰ、Ⅱ和Ⅲ。各区磁感应强度恒定, 大小不同,方向均垂直纸面向外。电子以初动能Ek0从圆b上P点沿径向进入电场。电 场可以反向,保证电子每次进入电场即被全程加速。已知圆a与圆b之间电势差为U,圆 b半径为R,圆c半径为 R,电子质量为m,电荷量为e。忽略相对论效应。取tan 22.5°=0.4。
 (1)当Ek0=0时,电子加速后均沿各磁场区边缘进入磁场,且在电场内相邻运动轨迹的夹 角θ均为45°,最终从Q点出射,运动轨迹如图中带箭头实线所示。求Ⅰ区的磁感应强度 大小、电子在Ⅰ区磁场中的运动时间及在Q点出射时的动能;
(2)已知电子只要不与Ⅰ区磁场外边界相碰,就能从出射区域出射。当Ek0=keU时,要保 证电子从出射区域出射,求k的最大值。答案    (1)            8eU    (2) 
14. (2021浙江6月选考,22,10分)如图甲所示,空间站上某种离子推进器由离子源、间距为d的中间有小孔的两平行金属板M、N和边长为L的立方体构成,其后端面P为喷 口。以金属板N的中心O为坐标原点,垂直立方体侧面和金属板建立x、y和z坐标轴。 M、N板之间存在场强为E、方向沿z轴正方向的匀强电场;立方体内存在磁场,其磁感 应强度沿z方向的分量始终为零,沿x和y方向的分量Bx和By随时间周期性变化规律如图 乙所示,图中B0可调。氙离子(Xe2+)束从离子源小孔S射出,沿z方向匀速运动到M板,经 电场加速进入磁场区域,最后从端面P射出。测得离子经电场加速后在金属板N中心 点O处相对推进器的速度为v0。已知单个离子的质量为m、电荷量为2e,忽略离子间的 相互作用,且射出的离子总质量远小于推进器的质量。
 (1)求离子从小孔S射出时相对推进器的速度大小vS;(2)不考虑在磁场突变时运动的离子,调节B0的值,使得从小孔S射出的离子均能从喷口 后端面P射出,求B0的取值范围;
(3)设离子在磁场中的运动时间远小于磁场变化周期T,单位时间从端面P射出的离子 数为n,且B0= ,求图乙中t0时刻离子束对推进器作用力沿z轴方向的分力。答案    (1)     (2)0~     (3)离子在立方体中运动轨迹的剖面图如图所示 洛伦兹力提供向心力,有2ev0( B0)= 且满足B0= 
解得R3= L,cs θ= 离子从端面P射出时,在沿z轴方向根据动量定理有FΔt=nΔt·mv0 cs θ-0根据牛顿第三定律可得离子束对推进器作用力沿z轴方向的分力大小为F'=F= nmv0,方向沿z轴负方向。
考点一　磁场对电流的作用
2. (2023届茂名冲刺模拟,10)(多选)如图所示,空间有一无限大、正交的匀强电场和匀强磁场,电场强度为E,方向竖直向下,磁感应强度为B,方向垂直于纸面向外,场中有 一内壁光滑竖直放置的绝缘长筒,其底部有一带电荷量为-q(q>0),质量为 的小球,g为重力加速度,小球直径略小于长筒内径。现长筒在外力作用下以大小为v0的速度向 右做匀速直线运动。已知小球刚离开长筒时小球在竖直方向的分速度大小为v0,下列 说法正确的是 (　    )
A.小球在长筒中的运动时间为 B.小球在长筒中的运动时间为 C.小球从长筒中飞出后做匀速圆周运动的轨道半径的大小为 D.小球从长筒中飞出后做匀速圆周运动的轨道半径的大小为 
3. (2023届潮州二模,16)如图所示,直角坐标系xOy所在竖直平面内,第一、第二象限中分布着沿x轴负方向的匀强电场E1,第三、第四象限中分布着沿y轴正方向的匀强 电场E2;第三、第四象限还分布着匀强磁场(图中未画出)。一质量为m、带电荷量为q 的带正电小球自坐标为(0,L)的A点由静止出发,进入第三象限后恰能做匀速圆周运动 并垂直于y轴射入第四象限,已知E1= ,重力加速度为g。求:(1)小球第一次通过x轴时的速度大小;(2)匀强电场的电场强度E2和匀强磁场的磁感应强度B大小的比值;(3)小球从第四象限穿出后,经过一段时间会再次到达x轴上的N点(图中未标出),求小球 从出发运动至N点的时间tAN。
4. (2024届潮州松昌中学摸底测,14)如图所示,M、N两金属圆筒是直线加速器的一部分,M与N的电势差为U;边长为2L的立方体区域内有竖直向上的匀强磁场。一质量 为m,电荷量为+q的粒子,以初速度v0水平进入圆筒M左侧的小孔。粒子在每个筒内均 做匀速直线运动,在两筒间做匀加速直线运动。粒子自圆筒N出来后,从正方形add'a' 的中心垂直进入磁场区域,最后由正方形abb'a'中心垂直飞出磁场区域,忽略粒子受到 的重力。求:(1)粒子进入磁场区域时的速率;(2)磁感应强度的大小。
5. (2023届河源期末,16)现代科技中常常利用电场和磁场来控制带电粒子的运动,某控制装置如图所示,区域Ⅰ中有 圆弧形均匀辐向电场,半径为R的弧线O'O处的场强大小处处相等,且大小为E1、方向指向圆心O1;在空间坐标系中,区域Ⅱ是边长为L的正方 体空间,该空间内充满沿y轴正方向的匀强电场E2(大小未知);区域Ⅲ也是边长为L的正 方体空间,空间内充满平行于xOy平面、与x轴负方向成45°角的匀强磁场,磁感应强度 大小为B,在区域Ⅲ的上表面是一粒子收集板;一群比荷不同的带正电粒子以不同的速 率先后从O'沿切线方向进入辐向电场,所有粒子都能通过辐向电场从坐标原点O沿x轴 正方向进入区域Ⅱ,不计带电粒子所受重力和粒子之间的相互作用。
(1)若某一粒子进入辐向电场的速率为v0,该粒子通过区域Ⅱ后刚好从P点进入区域Ⅲ 中,已知P点坐标为(L, ,0),求该粒子的比荷 和区域Ⅱ中电场强度E2的大小;(2)保持(1)问中E2不变,为了使粒子能够在区域Ⅲ中直接打到粒子收集板上,求粒子的
比荷 需要满足的条件。答案    (1)          (2) < < 
6. (2023届茂名一模,15)如图甲所示,空间存在方向竖直向上周期性变化的匀强电场,场强大小随时间变化如图乙所示,空间还存在方向垂直纸面向外的匀强磁场,磁感应 强度大小随时间变化如图丙所示。一个质量为0.1 kg、带电荷量为+0.2 C的小球,在t= 0时刻从空间P点在纸面内以水平向右大小为10 m/s的速度抛出。小球在空中运动的 时间大于2 s,最终落地时速度垂直于地面。重力加速度为10 m/s2,小球可视为质点,求:(1)t=1 s时,小球的速度大小;(2)1~2 s内小球受到的合力大小;(3)小球第一次速度水平向左时距P点的高度;(4)P点离地面的高度至少为多少。
微专题15　磁场与现代科技
1. (2023广东,5,4分)某小型医用回旋加速器,最大回旋半径为0.5 m,磁感应强度大小为1.12 T,质子加速后获得的最大动能为1.5×107 eV。根据给出的数据,可计算质子经该 回旋加速器加速后的最大速率约为(忽略相对论效应,1 eV=1.6×10-19 J) (　    )A.3.6×106 m/s　　　　　　　    B.1.2×107 m/sC.5.4×107 m/s　　　　　　　    D.2.4×108 m/s
4. (2024届佛山南海摸底,14)如图所示是某种质谱仪的结构简化图。质量为m、电荷量为+q的粒子束恰能沿直线通过速度选择器,并从环状D形盒的中缝(宽度略大于 粒子直径)射入磁感应强度为B0、方向垂直纸面向里的环形磁场区域。环状D形盒的 外半径为2R,内半径为R,外壳的厚度不计,出口M、N之间放置照相底片,底片能记录粒 子经过出口时的位置。已知速度选择器中电场强度大小为E,方向水平向左,磁感应强 度大小为B(磁场方向未画出)。不计粒子重力,若带电粒子能够打到照相底片,求:(1)B的方向以及粒子进入环状D形盒时的速度大小;(2)环状D形盒中的磁感应强度B0的大小范围。
5. (2021天津,12,18分)霍尔元件是一种重要的磁传感器,可用在多种自动控制系统中。长方体半导体材料厚为a、宽为b、长为c,以长方体三边为坐标轴建立坐标系xyz, 如图所示。半导体中有电荷量均为e的自由电子与空穴两种载流子,空穴可看作带正 电荷的自由移动粒子,单位体积内自由电子和空穴的数目分别为n和p。当半导体材料 通有沿+x方向的恒定电流后,某时刻在半导体所在空间加一匀强磁场,磁感应强度的 大小为B,沿+y方向,于是在z方向上很快建立稳定电场,称其为霍尔电场,已知电场强度 大小为E,沿-z方向。(1)判断刚加磁场瞬间自由电子受到的洛伦兹力方向;(2)若自由电子定向移动在沿+x方向上形成的电流为In,求单个自由电子由于定向移动
在z方向上受到洛伦兹力和霍尔电场力的合力大小Fnz;(3)霍尔电场建立后,自由电子与空穴在z方向定向移动的速率分别为vnz、vpz,求Δt时间 内运动到半导体z方向的上表面的自由电子数与空穴数,并说明两种载流子在z方向上 形成的电流应满足的条件。 
微专题16　磁场中的动态圆问题
7. (2020课标Ⅰ,18,6分)一匀强磁场的磁感应强度大小为B,方向垂直于纸面向外,其边界如图中虚线所示, 为半圆,ac、bd与直径ab共线,ac间的距离等于半圆的半径。一束质量为m、电荷量为q(q>0)的粒子,在纸面内从c点垂直于ac射入磁场,这些粒子具 有各种速率。不计粒子之间的相互作用。在磁场中运动时间最长的粒子,其运动时间 为 (　    ) 
A. 　     B. 　     C. 　     D. 
9. (2020浙江7月选考,22,10分)某种离子诊断测量简化装置如图所示。竖直平面内存在边界为矩形EFGH、方向垂直纸面向外、磁感应强度大小为B的匀强磁场,探测板 CD平行于HG水平放置,能沿竖直方向缓慢移动且接地。a、b、c三束宽度不计、间 距相等的离子束中的离子均以相同速度持续从边界EH水平射入磁场,b束中的离子在 磁场中沿半径为R的四分之一圆弧运动后从下边界HG竖直向下射出,并打在探测板的 右边缘D点。已知每束每秒射入磁场的离子数均为N,离子束间的距离均为0.6R,探测 板CD的宽度为0.5R,离子质量均为m,电荷量均为q,不计重力及离子间的相互作用。
(1)求离子速度v的大小及c束中的离子射出磁场边界HG时与H点的距离s;(2)求探测到三束离子时探测板与边界HG的最大距离Lmax;(3)若打到探测板上的离子被全部吸收,求离子束对探测板的平均作用力的竖直分量F 与板到HG距离L的关系。