



初中数学北师大版(2024)九年级上册第五章 投影与视图1 投影精品综合训练题
展开倍速学习四种方法
【方法一】 脉络梳理法
知识点1.投影与中心投影
知识点2平行投影(重点)
知识点3.中心投影和平行投影的异同点(难点)
知识点4.正投影(重点)
【方法二】 实例探索法
题型1.与中心投影有关的作图与计算
题型2.与平行投影有关的作图与计算
题型3.与正投影有关的计算
【方法三】 仿真实战法
考法. 投影下物体形状的判断
【方法四】 成果评定法
【学习目标】
1.了解投影、中心投影、平行投影、正投影的含义,会画物体在不同光线下的投影,会根据投影判断点光源的位置。
2.知道物体在灯光下与太阳光下的影子的不同特征以及不同时刻、不同位置影子的变化情况,体会灯光下的投影(中心投影)与太阳光下的投影(平行投影)的区别。
3.能利用投影和相似的知识解决某些实际生活中的问题。
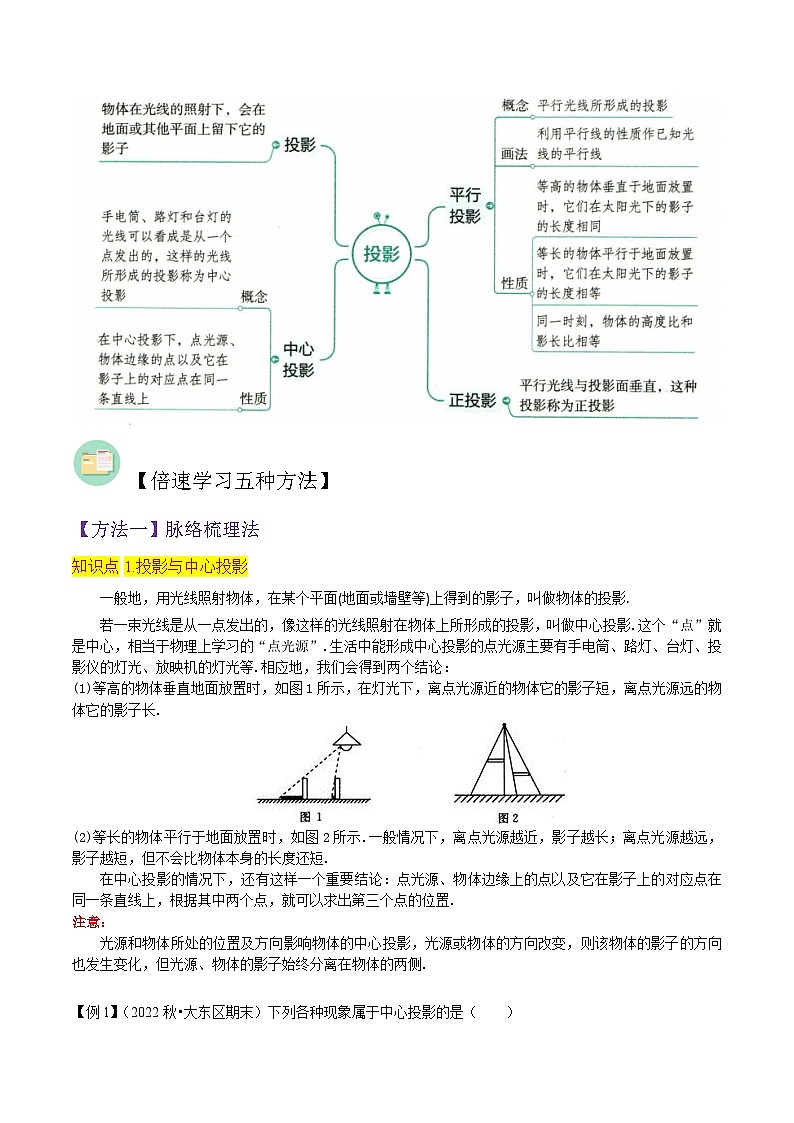
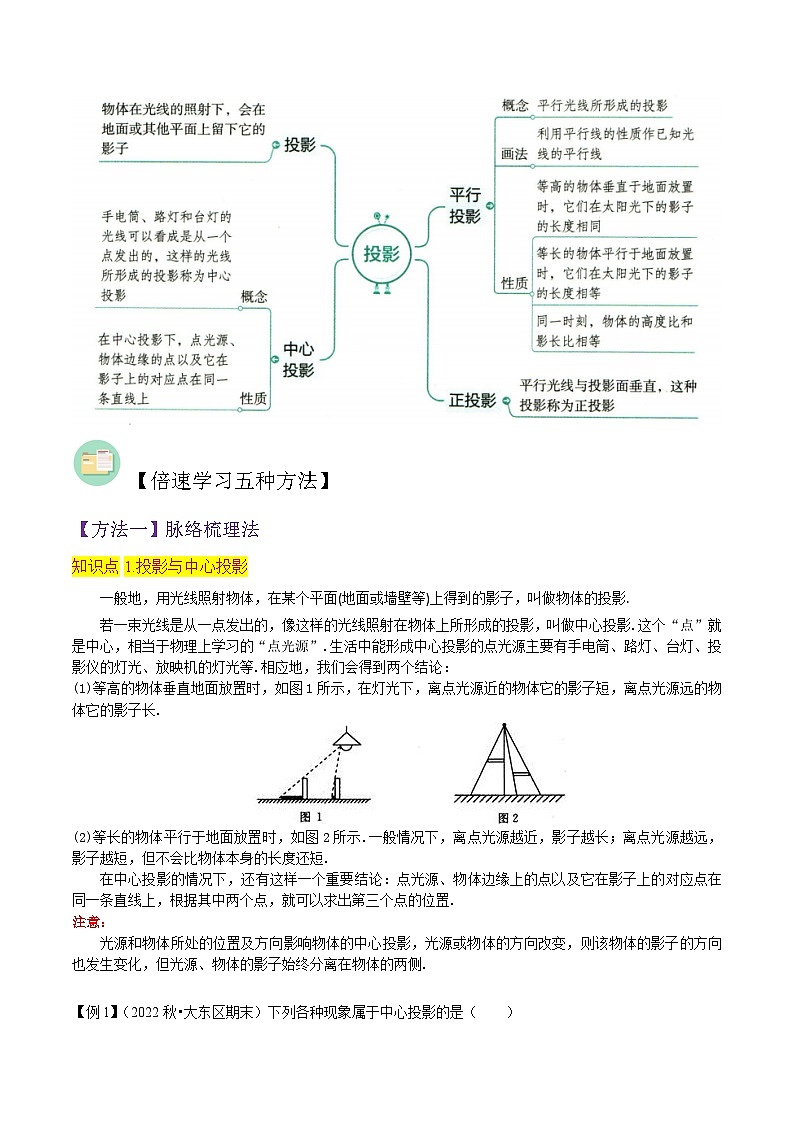
【知识导图】
【倍速学习五种方法】
【方法一】脉络梳理法
知识点1.投影与中心投影
一般地,用光线照射物体,在某个平面(地面或墙壁等)上得到的影子,叫做物体的投影.
若一束光线是从一点发出的,像这样的光线照射在物体上所形成的投影,叫做中心投影.这个“点”就是中心,相当于物理上学习的“点光源”.生活中能形成中心投影的点光源主要有手电筒、路灯、台灯、投影仪的灯光、放映机的灯光等.相应地,我们会得到两个结论:
(1)等高的物体垂直地面放置时,如图1所示,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
(2)等长的物体平行于地面放置时,如图2所示.一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
在中心投影的情况下,还有这样一个重要结论:点光源、物体边缘上的点以及它在影子上的对应点在同一条直线上,根据其中两个点,就可以求出第三个点的位置.
注意:
光源和物体所处的位置及方向影响物体的中心投影,光源或物体的方向改变,则该物体的影子的方向也发生变化,但光源、物体的影子始终分离在物体的两侧.
【例1】(2022秋•大东区期末)下列各种现象属于中心投影的是( )
A.晚上人走在路灯下的影子
B.中午用来乘凉的树影
C.上午人走在路上的影子
D.阳光下旗杆的影子
【变式】(2022秋•浦江县期末)如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m.则路灯的高度OP为( )
A.5mB.4.5mC.4mD.3m
知识点2平行投影(重点)
1.只要有光线,有被光线照到的物体,就存在影子.太阳光线可看做平行的,象这样的光线照射在物体上,所形成的投影叫做平行投影.由此我们可得出这样两个结论:
(1)等高的物体垂直地面放置时,如图1所示,在太阳光下,它们的影子一样长.
(2)等长的物体平行于地面放置时,如图2所示,它们在太阳光下的影子一样长,且影长等于物体本身的长度.
2. 物高与影长的关系
(1)在不同时刻,同一物体的影子的方向和大小可能不同.不同时刻,物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚,物体影子的指向是:西→西北→北→东北→东,影长也是由长变短再变长.
(2)在同一时刻,不同物体的物高与影长成正比例.
即:.
利用上面的关系式可以计算高大物体的高度,比如旗杆的高度等.
注意:利用影长计算物高时,要注意的是测量两物体在同一时刻的影长.
注意:
1.平行投影是物体投影的一种,是在平行光线的照射下产生的.利用平行投影知识解题要分清不同时刻和同一时刻.
2.物体与影子上的对应点的连线是平行的就说明是平行光线.
【例2】(2023春•和平区期末)如图,已知太阳光线AC和DE是平行的,在同一时刻,如果将两根高度相同的木杆竖直插在地面上,那么在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
A.SASB.AASC.SSSD.ASA
【变式】(2022秋•广宗县期末)如图所示,表示两棵小树在同一时刻阳光下的影子的图形可能是( )
A.B.
C.D.
知识点3.中心投影和平行投影的异同点(难点)
联系:
(1)中心投影、平行投影都是研究物体投影的一种,只不过平行投影是在平行光线下所形成的投影,通常的平行光线有太阳光线、月光等,而中心投影是从一点发出的光线所形成的投影,通常状况下,灯泡的光线、手电筒的光线等都可看成是从某一点发射出来的光线.
(2)在平行投影中,同一时刻改变物体的方向和位置,其投影也跟着发生变化;在中心投影中,同一灯光下,改变物体的位置和方向,其投影也跟着发生变化.在中心投影中,固定物体的位置和方向,改变灯光的位置,物体投影的方向和位置也要发生变化.
2.区别:
(1)太阳光线是平行的,故太阳光下的影子长度都与物体高度成比例;灯光是发散的,灯光下的影子与物体高度不一定成比例.
(2)同一时刻,太阳光下影子的方向总是在同一方向,而灯光下的影子可能在同一方向,也可能在不同方向.
注意:
在解决有关投影的问题时必须先判断准确是平行投影还是中心投影,然后再根据它们的具体特点进一步解决问题.
知识点4.正投影(重点)
正投影的定义:
如图所示,图(1)中的投影线集中于一点,形成中心投影;图(2)(3)中,投影线互相平行,形成平行投影;图(2)中,投影线斜着照射投影面;图(3)中投影线垂直照射投影面(即投影线正对着投影面),我们也称这种情形为投影线垂直于投影面.像图(3)这样,投影线垂直于投影面产生的投影叫做正投影.
(1)线段的正投影分为三种情况.如图所示.
①线段AB平行于投影面P时,它的正投影是线段A1B1,与线段AB的长相等;
②线段AB倾斜于投影面P时,它的正投影是线段A2B2,长小于线段AB的长;
③线段AB垂直于投影面P时,它的正投影是一个点.
(2)平面图形正投影也分三种情况,如图所示.
①当平面图形平行于投影面Q时,它的正投影与这个平面图形的形状、大小完全相同,即正投影与这个平面图形全等;
②当平面图形倾斜于投影面Q时,平面图形的正投影与这个平面图形的形状、大小发生变化,即会缩小,是类似图形但不一定相似.
③当平面图形垂直于投影面Q时,它的正投影是直线或直线的一部分.
(3)立体图形的正投影.
物体的正投影的形状、大小与物体相对于投影面的位置有关,立体图形的正投影与平行于投影面且过立体图形的最大截面全等.
注意:
(1)正投影是特殊的平行投影,它不可能是中心投影.
(2)由线段、平面图形和立体图形的正投影规律,可以识别或画出物体的正投影.
(3)由于正投影的投影线垂直于投影面,一个物体的正投影与我们沿投影线方向观察这个物体看到的图象之间是有联系的.
【例3】(2023·江苏南通·校考三模)一个正五棱柱如下图摆放,光线由上到下照射此正五棱柱时的正投影是( )
A.B.C.D.
【变式】(2023·湖北恩施·校考模拟预测)物体正投影的形状、大小与它相对于投影面的位置有关.一个三角板的正投影不可能是( )
A.一条线段B.一个与原三角板全等的三角形
C.一个等腰三角形D.一个小圆点
【方法二】实例探索法
题型1.与中心投影有关的作图与计算
1.(2022秋•宝安区校级期中)如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
2.(2023•三水区校级开学)如图,在平面直角坐标系中,点P(4,3)是一个光源,CD为木杆AB在x轴上的投影,A(0,1),B(6,1),过点P作PM⊥x轴,垂足为点M,PM交AB于点N,求CD的长.
3.(2022秋•市北区期末)如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一棵大树,它在这个路灯下的影子是MN.
(1)在图中画出路灯的位置并用点P表示;
(2)在图中画出表示大树的线段MQ.
4.(2022春•连山区月考)如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发现自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.
(1)找出路灯的位置.
(2)估计路灯的高,并求影长PQ.
题型2.与平行投影有关的作图与计算
5.(2022秋•临渭区期末)如图,AB和DE是直立在地面上的两根立柱,已知AB=5m,某一时刻AB在太阳光下的影子长BC=3m.
(1)在图中画出此时DE在太阳光下的影子EF;
(2)在测量AB的影子长时,同时测量出EF=6m,计算DE的长.
6.(2022秋•榆阳区校级期末)如图,小亮利用所学的数学知识测量某旗杆AB的高度.
(1)请你根据小亮在阳光下的投影,画出旗杆AB在阳光下的投影.
(2)已知小亮的身高为1.72m,在同一时刻测得小亮和旗杆AB的投影长分别为0.86m和6m,求旗杆AB的高.
7.(2023•市北区开学)甲、乙两栋楼的位置如图所示,甲楼AB高16米.当地中午12时,物高与影长的比是1:.
(1)如图1,当地中午12时,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为 米.
(2)当地下午14时,物高与影长的比是1:2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.
8.(2022秋•榕城区期末)如图,某数学兴趣小组要测量学校旗杆的高度,在某一时刻测得1 m长的竹竿竖直放置时影长为1.5 m,在同时刻测量旗杆的影长时,因旗杆靠近一教学楼,影子不全落在地面上,有一部分落在墙上,测得落在地面上的影长为18 m,留在墙上的影高为3 m,求旗杆的高度.
题型3.与正投影有关的计算
9.(2023春·九年级单元测试)如图,正方形纸板在投影面上的正投影为,其中边与投影面平行,与投影面不平行.若正方形的边长为5厘米,,求其投影的面积.
10.(2023春·四川自贡·九年级四川省荣县中学校校考阶段练习)操作与研究∶如图,被平行于的光线照射,于,在投影面上.
(1)指出图中的投影是什么,与的投影呢?
(2)探究∶ 如图1,中,,,我们可以利用与相似证明, 这个结论我们称之为射影定理,试证明这个定理.
(3)【结论运用】如图2,正方形的边长为,点是对角线的交点,点在上,过点作,垂足为,连接,
①试利用射影定理证明;
②若,求的长.
【方法三】 仿真实战法
考法. 投影下物体形状的判断
1.(2021•南京)如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A.B.C.D.
2.(2017•贺州)小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A.B.
C.D.
【方法四】 成果评定法
一、单选题
1.(2022春·河北保定·九年级保定市第十七中学校考开学考试)下列光线所形成的投影是平行投影的是( )
A.太阳光线B.台灯的光线C.手电筒的光线D.路灯的光线
2.(2023·河南信阳·二模)小明利用一面镜子把太阳光经镜子反射后,光线平行于地面照到了墙上,如图镜子与地面夹角为,则太阳光与地面所成角度是( )
A.B.C.D.
3.(2022秋·湖南株洲·九年级统考期中)某一时刻太阳光下身高的小明的影长为2m,同一时刻旗杆的影长为6m则旗杆的高度为( )
A.B.8mC.D.7m
4.(2023春·山东临沂·九年级校考阶段练习)如图,一束太阳光线平行照射在放置于地面的正五边形,若,则( )
A.56°B.66°C.72°D.76°
5.(2023·江苏无锡·统考二模)如图,在平面直角坐标系中,点是一个光源.木杆两端的坐标分别为,.则木杆在x轴上的投影长为( )
A.B.C.5D.6
6.(2023·河北沧州·校考模拟预测)幻灯机是教师常用的教具之一,它能把精致的图片投到银幕上,如图,在与中,下列结论一定正确的是( )
A.B.C.D.
7.(2023春·山东泰安·九年级校考阶段练习)下列各种现象属于中心投影现象的是( )
A.早上升旗时地面上旗杆的影子B.上午人走在路上的影子
C.中午用来乘凉的树影D.晚上人走在路灯下的影子
8.(2022·河北石家庄·校联考三模)如图,在平面直角坐标系中,点是一个光源,木杆两端的坐标分别为,,则木杆在x轴上的投影长为( )
A.B.C.5D.6
9.(2022·广东广州·统考二模)当下,户外广告已对我们的生活产生直接的影响.图中的是安装在广告架上的一块广告牌,和分别表示太阳光线.若某一时刻广告牌在地面上的影长,在地面上的影长,广告牌的顶端A到地面的距离,则广告牌的高为( )
A.B. C.D.
10.(2023春·九年级单元测试)在平面直角坐标系中,点是一个光源,木杆两端的坐标分别是,,则木杆在x轴上的投影的长是( )
A.4B.C.D.5
二、填空题
11.(2022春·九年级单元测试)正午时我们在太阳下的影子长度比下午时我们在太阳底下的影子的长度要 .(长,短)
12.(2023春·九年级单元测试)由阳光形成的影子是 投影,由灯光形成的影子是 投影(选题“平行”或“中心”)
13.(2023·湖南长沙·校联考二模)身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到米,米,则旗杆的高度是
14.(2023春·九年级单元测试)在相同时刻太阳光线是平行的,如果高米的测杆影长3米,那么此时影长米的旗杆的高度为 m
15.(2023春·吉林长春·九年级校考阶段练习)如图,小明晚上由路A下的B处走到C处时,测得影子的长为1米,继续往前走3米到达E处时,测得影子的长为2米,已知小明的身高是米,那么路灯的高度等于 米.
16.(2023·全国·九年级专题练习)小华家客厅有一张直径为,高为的圆桌,有一盏灯到地面垂直距离为,圆桌的影子为,则点到点的距离为 .
17.(2023·浙江台州·统考一模)公元前6世纪,古希腊学者泰勒斯用图1的方法巧测金字塔的高度.如图2,小明仿照这个方法,测量圆锥形小山包的高度,已知圆锥底面周长为.先在小山包旁边立起一根木棒,当木棒影子长度等于木棒高度时,测得小山包影子长为(直线过底面圆心),则小山包的高为 (取).
18.(2023·浙江·一模)日晷是我国古代利用日影测定时刻的一种计时仪器,它由“晷面”和“晷针”组成,古人常用的日晷有水平式日晷(图1)和赤道式日晷(图2).其中水平式日晷的“晷针”与“晷面”的夹角就是其所在位置的地理纬度且“晷面”与地面平行;赤道式日晷的“晷面”与赤道面平行当太阳光照在日晷上时,晷针的影子就会投向晷面.随着时间的推移,晷针的影子在晷面上慢慢地移动,以此来显示时刻.此外,水平式日晷的“晷面”刻度不均匀,赤道式日晷的“晷面”刻度则是均匀的.
(1)如图1,当水平式日晷放在纬度为 (即)位置时,晷针与晷面的夹角为 °.
(2)如图3,将两种日晷的“晷针”重合,n小时后,两种日晷对应的时刻一致,即两种晷“晷针”的影子所在的直线相交于点.此时与满足的关系式 .
三、解答题
19.(2020秋·广东清远·九年级统考期末)小红想利用阳光下的影长测量学校旗杆的高度.如图,他在某一时刻在地面上竖直立一个2米长的标杆,测得其影长米.
(1)请在图中画出此时旗杆在阳光下的投影.
(2)如果,求旗杆的高.
20.(2022秋·辽宁丹东·九年级统考期末)如图,身高米的小明站在处,路灯底部到的距离为米,此时小明的影长米.
(1)请在图中画出表示路灯高的线段并求出路灯的高度;
(2)小明沿所在直线又行走了一段距离到达处,请在图中画出表示小明在处时影长的线段.
21.(2023秋·广东茂名·九年级统考期末)小红想利用阳光下的影长测量学校旗杆的高度,如图,他在某一时刻在地面上竖直立一个2m长的标杆,测得其影长m.
(1)请在图中画出此时旗杆在阳光下的投影;
(2)如果m,求旗杆的高.
22.(2023春·河南信阳·九年级校考阶段练习)阳光明媚的天,实践课上,亮亮准备用所学的知识测量教学楼前一座假山AB的高度,如图,亮亮在地面上的点F处,眼睛贴地观察,看到假山顶端A、教学楼顶端C在一条直线上.此时他起身在F处站直,发现自己的影子末端和教学楼的影子末端恰好重合于点G处,测得米,亮亮的身高EF为1.6米.假山的底部B处因有花园围栏,无法到达,但经询问和进行部分测量后得知,米,点D、B、F、G在一条直线上,,,,已知教学楼的高度为16米,请你求出假山的高度.
23.(2022秋·陕西西安·九年级校联考期中)李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
24.(2022春·全国·九年级专题练习)小明在晚上由路灯走向路灯,当他走到处时,发现身后影子顶部正好触到路灯底部,当他向前再步行到达时,发现他的影子的顶点正好接触到路灯的底部.已知小明的身高是,两个路灯的高度都是,且.
(1)求:两个路灯之间的距离;
(2)小明在两个路灯之间行走时,在两个路灯下的影长之和是否为定值?如果是定值,直接写出此定值,如果不是定值,求说明理由.
25.(2023·全国·九年级专题练习)甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量,下面是他们通过测量得到的一些信息:
甲组:如图①,测得一根直立于平地、长为80cm的竹竿的影长为60cm.
乙组:如图②,测得学校旗杆的影长为900cm.
丙组:如图③,测得校园景灯?(灯罩视为圆柱体,灯杆粗细忽略不计)的灯罩部分影长为90cm,灯杆被阳光照射到的部分长为50cm,未被照射到的部分长为32cm.
(1)请你根据甲、乙两组得到的信息计算出学校旗杆的高度.
(2)请根据甲、丙两组得到的信息,解答下列问题:
①求灯罩底面半径的长;
②求从正面看灯罩得到的图形的面积和从上面看灯罩得到的图形的面积.
26.(2023·山东日照·校考一模)操作与研究:如图,被平行于的光线照射,于D,在投影面上.
(1)指出图中线段的投影是______,线段的投影是______.
(2)问题情景:如图1,中,,,我们可以利用与相似证明,这个结论我们称之为射影定理,请证明这个定理.
(3)【结论运用】如图2,正方形的边长为15,点O是对角线的交点,点E在上,过点C作,垂足为F,连接,
①试利用射影定理证明;
②若,求的长.
北师大版(2024)九年级上册3 反比例函数的应用优秀课堂检测: 这是一份北师大版(2024)九年级上册<a href="/sx/tb_c99915_t7/?tag_id=28" target="_blank">3 反比例函数的应用优秀课堂检测</a>,文件包含专题22反比例函数的应用2个知识点2种题型2种中考考法原卷版docx、专题22反比例函数的应用2个知识点2种题型2种中考考法解析版docx等2份试卷配套教学资源,其中试卷共80页, 欢迎下载使用。
北师大版(2024)九年级上册1 反比例函数精品练习题: 这是一份北师大版(2024)九年级上册<a href="/sx/tb_c99913_t7/?tag_id=28" target="_blank">1 反比例函数精品练习题</a>,文件包含专题20反比例函数3个知识点4种题型1种中考考法原卷版docx、专题20反比例函数3个知识点4种题型1种中考考法解析版docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。
北师大版(2024)九年级上册2 视图精品复习练习题: 这是一份北师大版(2024)九年级上册<a href="/sx/tb_c99911_t7/?tag_id=28" target="_blank">2 视图精品复习练习题</a>,文件包含专题19视图5个知识点2种题型2种中考考法原卷版docx、专题19视图5个知识点2种题型2种中考考法解析版docx等2份试卷配套教学资源,其中试卷共79页, 欢迎下载使用。













