
高中数学3.1 函数同步测试题
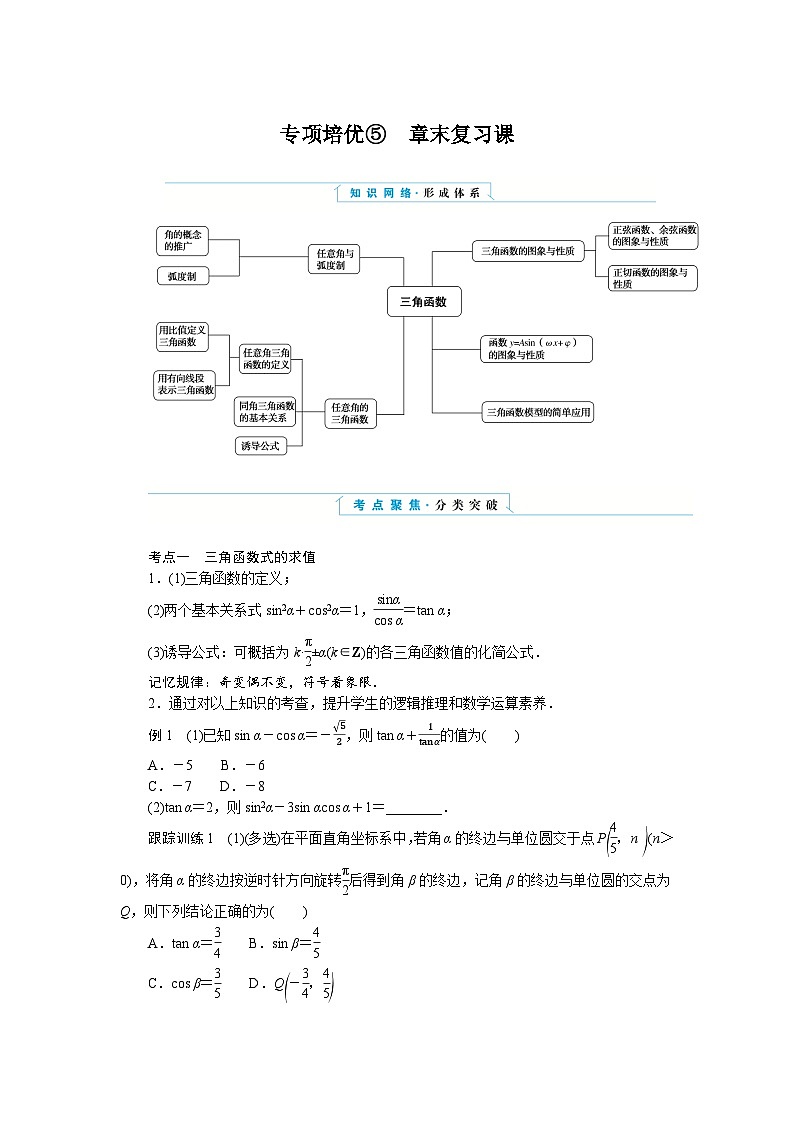
展开考点一 三角函数式的求值
1.(1)三角函数的定义;
(2)两个基本关系式sin2α+cs2α=1, eq \f(sinα,cs α) =tan α;
(3)诱导公式:可概括为k· eq \f(π,2) ±α(k∈Z)的各三角函数值的化简公式.
记忆规律:奇变偶不变,符号看象限.
2.通过对以上知识的考查,提升学生的逻辑推理和数学运算素养.
例1 (1)已知sin α-cs α=-52,则tan α+1tanα的值为( )
A.-5 B.-6
C.-7 D.-8
(2)tan α=2,则sin2α-3sin αcs α+1=________.
跟踪训练1 (1)(多选)在平面直角坐标系中,若角α的终边与单位圆交于点P eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,5),n)) (n>0),将角α的终边按逆时针方向旋转 eq \f(π,2) 后得到角β的终边,记角β的终边与单位圆的交点为Q,则下列结论正确的为( )
A.tan α= eq \f(3,4) B.sin β= eq \f(4,5)
C.cs β= eq \f(3,5) D.Q eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(3,4),\f(4,5)))
(2)若cs (π+α)=-35,3π2<α<2π,则sin (2π-α)=________.
考点二 三角函数的图象
1.函数y=A sin (ωx+φ)的图象
(1)“五点法”作图;
(2)图象的识别;
(3)图象伸缩、平移变换;
(4)由函数图象求三角函数解析式.
2.通过对以上知识的考查,提升学生的直观想象和数学运算素养.
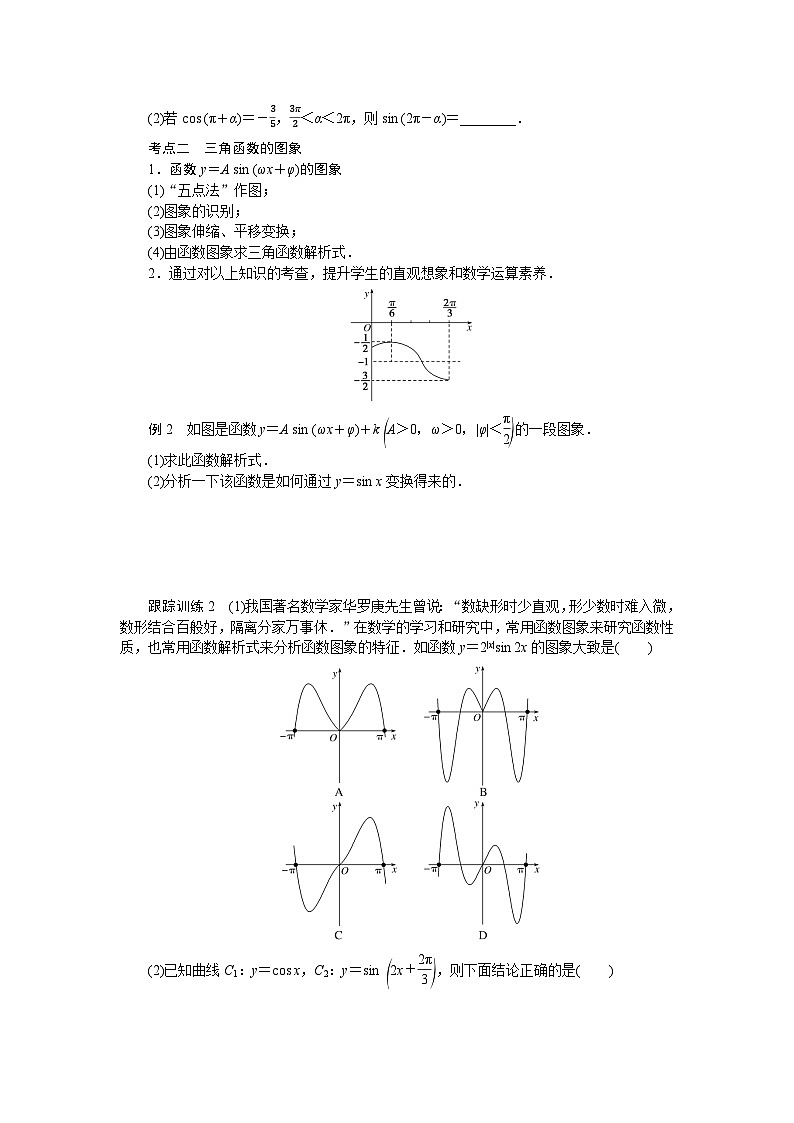
例2 如图是函数y=A sin (ωx+φ)+k eq \b\lc\(\rc\)(\a\vs4\al\c1(A>0,ω>0,|φ|<\f(π,2))) 的一段图象.
(1)求此函数解析式.
(2)分析一下该函数是如何通过y=sin x变换得来的.
跟踪训练2 (1)我国著名数学家华罗庚先生曾说:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休.”在数学的学习和研究中,常用函数图象来研究函数性质,也常用函数解析式来分析函数图象的特征.如函数y=2|x|sin 2x的图象大致是( )
(2)已知曲线C1:y=cs x,C2:y=sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(2π,3))) ,则下面结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 eq \f(π,6) 个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 eq \f(π,12) 个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的 eq \f(1,2) 倍,纵坐标不变,再把得到的曲线向右平移 eq \f(π,6) 个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的 eq \f(1,2) 倍,纵坐标不变,再把得到的曲线向左平移 eq \f(π,12) 个单位长度,得到曲线C2
考点三 三角函数的性质
1.三角函数的性质包括定义域、值域、单调性、奇偶性、对称性等,在研究性质时,将ωx+φ看成一个整体,利用整体代换思想解题是常见的技巧.
2.通过对以上知识的考查,提升学生的逻辑推理和数学运算素养.
例3 (1)(多选)设函数f(x)=2sin(2x+π2),则关于函数y=f(x)说法正确的是( )
A.函数y=f(x)是偶函数
B.函数y=f(x)在(0,π2)上单调递减
C.函数y=f(x)的最大值为2
D.函数y=f(x)图象关于点(π4,0)对称
(2)设函数f(x)=sin(2ωx−π6)的图象关于直线x=π对称,其中ω为常数,且ω∈(12,1).
①求函数f(x)的解析式;
②将函数f(x)的图象向右平移π10个单位长度后,再将得到的图象上各点的横坐标缩短到原来的56倍,得到函数y=g(x)的图象,若关于x的方程g(x)+k=0在区间[0,π2]上有实数解,求实数k的取值范围.
跟踪训练3 (1)(多选)下列说法中正确的是( )
A.函数y=sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,2))) 是偶函数
B.存在实数α,使 sin α cs α=1
C.直线x= eq \f(π,8) 是函数y=sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(5π,4))) 图象的一条对称轴
D.若α,β都是第一象限角,且α>β,则sin α>sin β
(2)设函数f(x)=12sin(2x-π3),
①求f(x)的最小正周期和单调递增区间;
②当x∈[π12,π2]时,求函数f(x)的最大值和最小值.
参考答案与解析
考点聚集·分类突破
例1 解析:(1)由题意可得(sin α-cs α)2=sin2α+cs2α-2sinαcs α=1-2sin αcs α=54,故sin αcs α=-18,切化弦可得tan α+1tanα=sinαcsα+csαsinα=sin2α+cs2αsinαcsα=1sinαcsα=-8.故选D.
(2)sin2α-3sinαcs α+1=sin2α-3sinαcs α+(sin2α+cs2α)
=2sin2α-3sinαcs α+cs2α
=2sin2α−3sinαcsα+cs2αsin2α+cs2α
=2tan2α−3tanα+1tan2α+1=2×22−3×2+122+1=35.
答案:(1)D (2)35
跟踪训练1 解析:(1)由角α的终边与单位圆交于点P45,n(n>0),α是第一象限角,可得csα=45,
∴sin α=1−cs2α=35,可得tanα=sinαcsα=34,故A正确;
将角α的终边按逆时针方向旋转π2后得到角β的终边,可得β=α+π2,
则可得sin β=sin α+π2=cs α=45,cs β=cs α+π2=-sin α=-35,故B正确,C错误;
据三角函数定义可得,角β的终边与单位圆的交点为Q,则点Q的坐标为−35,45,故D错误.故选AB.
(2)因为cs (π+α)=-35,所以-cs α=-35,可得cs α=35,
因为3π2<α<2π,所以sin α=-1−cs2α=-1−352=-45,
所以sin(2π-α)=-sin α=45.
答案:(1)AB (2)45
例2 解析:(1)由题图知A=−12−−322=12,
k=−12+−322=-1,
T=2×2π3−π6=π,
所以ω=2πT=2.所以y=12sin (2x+φ)-1.
当x=π6时,2×π6+φ=π2+2kπ,k∈Z,
又|φ|<π2,所以φ=π6.
综上,所求函数解析式为y=12sin 2x+π6-1.
(2)把y=sin x向左平移π6个单位,得到y=sin x+π6;然后纵坐标保持不变,横坐标缩短为原来的12,得到y=sin 2x+π6;再使横坐标保持不变,纵坐标变为原来的12,得到y=12sin 2x+π6,最后把函数y=12sin 2x+π6的图象向下平移1个单位,得到y=12sin 2x+π6-1的图象.
跟踪训练2 解析:(1)f(-x)=2|-x|sin (-2x)=-2|x|sin 2x=-f(x),函数为奇函数,图象关于原点对称,排除A,B,
当π2<x<π时,f(x)<0,排除C,
故选D.
(2)因为y=sin 2x+2π3=cs 2x+2π3−π2=cs 2x+π6,所以曲线C1:y=cs x上各点的横坐标缩短到原来的12倍,纵坐标不变,得到曲线y=cs 2x,再把得到的曲线y=cs 2x向左平移π12个单位长度,得到曲线y=cs 2x+π12=cs 2x+π6.故选D.
答案:(1)D (2)D
例3 解析:(1)∵函数f(x)=2sin 2x+π2=2cs 2x,
∴f(x)=2cs 2x,
∵f(-x)=2cs (-2x)=2cs 2x=f(x),y=f(x)为偶函数,故A正确;
令2kπ≤2x≤π+2kπ(k∈Z),解得kπ≤x≤π2+kπ(k∈Z),可得函数y=f(x)在0,π2单调递减,所以B正确;
由于f(x)的最大值是2,故选项C不符合题意.
由2x=kπ+π2,k∈Z,解得x=kπ2+π4,k∈Z,可得当k=0时,其图象关于点π4,0对称,故D正确.
解析:(2)①∵图象关于直线x=π对称,∴2πω-π6=π2+kπ,k∈Z
∴ω=k2+13,又ω∈12,1,
令k=1时,ω=56符合要求,
∴函数f(x)=sin 53x−π6.
②将函数f(x)的图象向右平移π10个单位长度后,得到函数y=sin 53x−π3的图象,再将得到的图象上各点的横坐标缩短到原来的56倍(纵坐标不变),得到函数y=sin 2x−π3的图象,所以g(x)=sin 2x−π3.
当0≤x≤5π12,即-π3≤2x-π3≤π2时,g(x)递增,g(x)∈−32,1,
当5π12
因为g(x)+k=0在区间0,π2上有实数解,
所以实数k的取值范围是−1,32.
答案:(1)ABD (2)见解析
跟踪训练3 解析:(1)对于A:函数y=sin x+π2=cs x,故该函数是偶函数,故A正确;
对于B:由于 sin α cs α=1,故sin α和cs α互为倒数,与sin2α+cs2α=1矛盾,故不存在实数α,使sin α cs α=1,故B错误;
对于C:当x=π8时,f(π8)=sin π4+5π4=-1,故C正确;
对于D:设α=13π6,β=π3,由于α,β都是第一象限角,但是sin β>sin α,故D错误;故选AC.
(2)①因为f(x)=12sin 2x−π3
所以f(x)的最小正周期是T=2π2=π,
由-π2+2kπ≤2x-π3≤π2+2kπ,k∈Z,解得-π12+kπ≤x≤5π12+kπ,k∈Z,
所以函数的单调递增区间为−π12+kπ,5π12+kπ,k∈Z.
②当x∈π12,π2时,2x-π3∈−π6,2π3,
此时sin 2x−π3∈−12,1,可得f(x)∈−14,12,
综上,f(x)最大值为12,最小值为-14.
答案:(1)AC (2)见解析
人教A版 (2019)必修 第一册5.4 三角函数的图象与性质课后测评: 这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质课后测评,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年5.2 三角函数的概念课时练习: 这是一份2020-2021学年5.2 三角函数的概念课时练习,共3页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
数学人教A版 (2019)5.2 三角函数的概念课堂检测: 这是一份数学人教A版 (2019)5.2 三角函数的概念课堂检测,共3页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













