



湘教版(2019)选择性必修 第一册第4章 计数原理4.1 两个计数原理教学演示课件ppt
展开1.在分类加法计数原理中,每类办法中的不同方法都能完成这件事吗?能.每一类办法中的每一种方法都能独立完成这件事,所以在分类时要做到不重 不漏.2.在分步乘法计数原理中,若某件事是分两步完成的,则其中任何一个单独的步骤 都能完成这件事吗?不能.每个步骤都完成才算完成这件事,即分步要做到“步骤完整”.
1.合理选择两个计数原理当完成一件事可以分为相互排斥的几类时,选择分类加法计数原理;当完成一件 事可以分为几个相互关联的步骤时,选择分步乘法计数原理.在求解过程中要注 意列举法、树状图法、间接法等的灵活应用.2.类中有步,步中有类问题 从A→D共有m1×(m2+m3+m4)×m5种方法.
1 两个计数原理的选择与应用
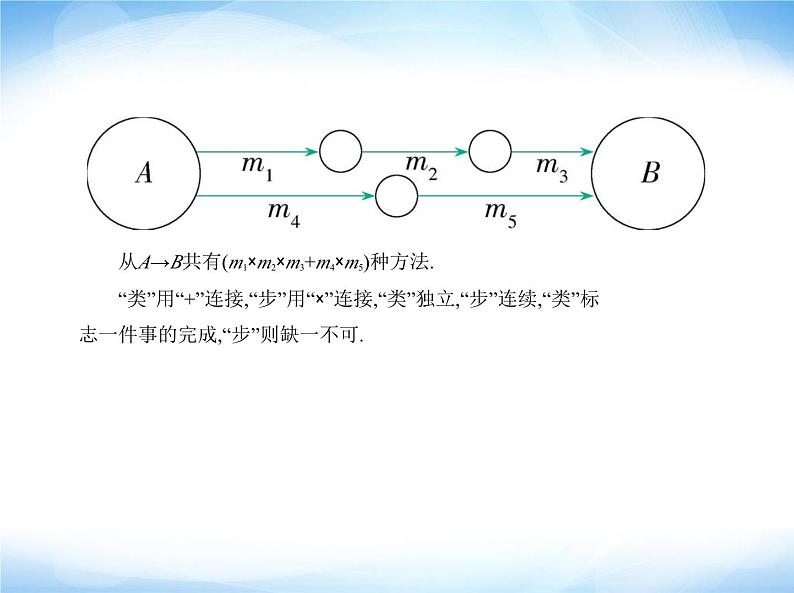
从A→B共有(m1×m2×m3+m4×m5)种方法. “类”用“+”连接,“步”用“×”连接,“类”独立,“步”连续,“类”标 志一件事的完成,“步”则缺一不可.
典例 若直线方程Ax+By=0中的A,B可以从0,1,2,3,5这五个数字中任取两个不同的数字,求该方程所表示的不同直线的条数.
思路点拨 以A,B中是否有数字0为标准进行分类计数,或利用间接法求解.
解析 解法一:分两类.第一类:当A,B中有一个为0时,方程表示直线x=0或y=0,共2条不同的直线.第二类:当A,B都不为0时,确定直线Ax+By=0需要分两步完成.第一步:确定A的值,有4种不同的取法;第二步:确定B的值,有3种不同的取法.所以该方程所表示的不同直线的条数为2+4×3=14.解法二(间接法):分两步.第一步:确定A的值,有5种不同的取法;第二步:确定B的值,有4种不同的取法.根据分步乘法计数原理,可以确定直线的条数为5×4=20.在这20条直线中,当A=0,B=1,2,3,5时,
表示同一条直线:y=0;当B=0,A=1,2,3,5时,表示同一条直线:x=0,即有6条直线是重复计数的.故该方程所表示的不同直线的条数为20-6=14.
涂色问题的两种解决方案(1)选择正确的涂色顺序,按步骤逐一涂色,应用分步乘法计数原理进行计算;(2)先根据涂色时所用颜色种数进行分类处理,再在每一类的涂色方法数的计算 中应用分步乘法计数原理,最后根据分类加法计数原理对每一类的涂色方法数求 和,即得到最终的涂色方法数.
典例 从红、黄、绿、黑四种颜色中选其中几种涂在如图所示的五个区域中,若要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?
选择性必修 第一册4.1 两个计数原理课堂教学课件ppt: 这是一份选择性必修 第一册4.1 两个计数原理课堂教学课件ppt,共31页。PPT课件主要包含了新知初探•课前预习,题型探究•课堂解透,m1+m2++mn,m1×m2××mn,答案C,答案D,答案A等内容,欢迎下载使用。
湘教版(2019)选择性必修 第一册4.1 两个计数原理教学ppt课件: 这是一份湘教版(2019)选择性必修 第一册4.1 两个计数原理教学ppt课件,共32页。PPT课件主要包含了目录索引等内容,欢迎下载使用。
数学选择性必修 第一册4.1 两个计数原理作业课件ppt: 这是一份数学选择性必修 第一册4.1 两个计数原理作业课件ppt,共19页。













