青岛版（2024）九年级上册3.1 圆的对称性完整版教学课件ppt

这是一份青岛版（2024）九年级上册3.1 圆的对称性完整版教学课件ppt，共30页。

如图，在一个平面内，线段（OA）绕它固定的一个端点（O）旋转一周，另一个端点（A）所形成的图形叫做圆．
1.经历利用画图、折叠探索圆的轴对称性的过程，理解圆的轴对称性。2.利用圆的轴对称性探究垂径定理，并能进行证明或运用。3.通过观察、比较、操作、推理、归纳等过程，发展合情推理能力。
1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
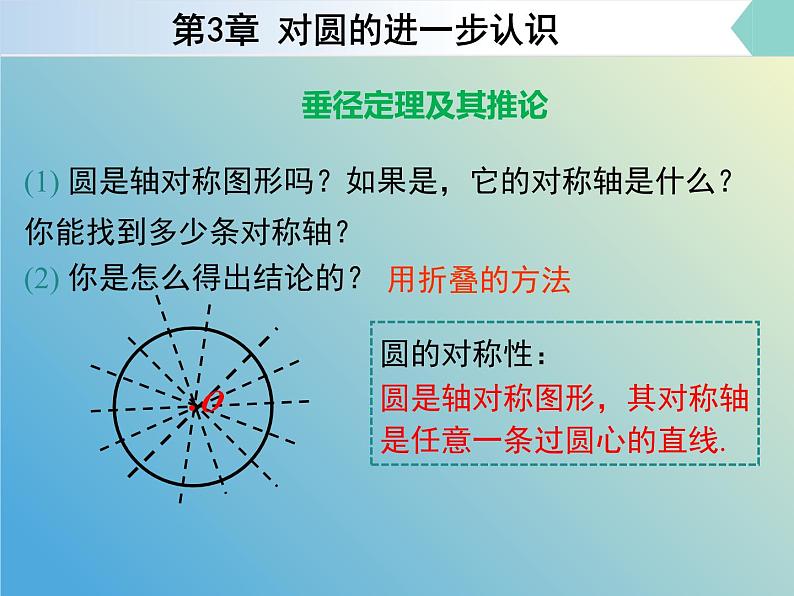
1、圆是轴对称图形吗？
2、如果是,它的对称轴是什么? 你能找到多少条对称轴？
3、你是用什么方法解决上述 问题的?
圆的轴对称性： 圆是轴对称图形，每一条直径所在的直线都是它的对称轴。
(1) 圆是轴对称图形吗？如果是，它的对称轴是什么？你能找到多少条对称轴？
(2) 你是怎么得出结论的？
圆的对称性： 圆是轴对称图形，其对称轴是任意一条过圆心的直线.
问题：如图，AB 是⊙O 的一条弦，直径 CD⊥AB， 垂足为 P. 你能发现图中有哪些相等的线段和劣弧?为什么?
温馨提示：垂径定理是圆中一个重要的定理，三种语言要相互转化，形成整体，才能运用自如.
垂直于弦的直径平分弦，并且平分弦所对的两条弧.
∵ CD 是⊙O 的直径，CD⊥AB，(条件)
【提问】下列图形是否具备垂径定理的条件？为什么？
弦心距：圆心到弦的距离（即圆心到弦的垂线段的距离）．
见弦常作弦心距，连接半径，构造直角三角形用勾股定理求解
满足其中任两条，必定同时满足另三条
（1）一条直线过圆心（2）这条直线垂直于弦（3）这条直线平分不是直径的弦（4）这条直线平分不是直径的弦所 对的优弧（5）这条直线平分不是直径的弦所 对的劣弧
（2）画⊙O的任一条弦AB,并取AB的中点M.
你能发现图中① CD 与 AB位置关系吗？ ②还有有哪些等量关系?
（3）过点M作直径CD.
平分弦（不是直径）的直径垂直于弦,并且平 分弦所对的两条弧.
（1）每人任意画一个圆；
你可以写出相应的命题吗?相信自己是最棒的!
如图,在下列五个条件中:
只要具备其中两个条件,是否可推出其余三个结论？
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
例1.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD.求证：OA=OB.证明:作OE⊥AB,垂足为点E.由垂径定理,得 CE=DE.∵AC=BD∴AC+CE=BD+DE,即AE=BE.∴OE为线段AB的垂直平分线.∴OA=OB.
例2.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).
你是第一个告诉同学解题方法和结果的吗？
解：如图，用 表示桥拱， 所在圆的圆心为O，半径为Rm，经过圆心O作弦AB的垂线OD，D为垂足，与 相交于点C.根据垂径定理，D是AB的中点，C是 的中点，CD就是拱高.由题设
在Rt△OAD中，由勾股定理，得
解得 R≈27.9（m）.
答：赵州石拱桥的桥拱半径约为27.9m.
解决有关弦的问题，经常过圆心作弦的垂线，或作垂直于弦的直径，并构造半径等辅助线，为应用垂径定理创造条件.
1.如图,已知在以O为圆心的三个同心圆中,AB,CD为大圆的 直径且AB⊥CD,大圆的半径OA=4 cm,则图中阴影部分的面 积是(　    )A.π cm2　　　    B.2π cm2C.3π cm2　　　    D.4π cm2
2.(新独家原创)(连半径法)如图,☉O的弦AB垂直平分半径 OC.若OC=2,则弦AC的长为(M9103001)(　    ) A. 　　　    B.2　　　    C.2 　　　    D.2 
解析　如图,连接OA,OB,BC, ∵弦AB垂直平分半径OC,∴AE=BE,即OC与AB互相垂直平 分,∴四边形OACB是菱形,∴AC=OA.∵☉O的半径为2,∴OA =AC=2.故选B.
方法解读　连半径法　同圆或等圆的半径相等,通过连半径 可以构造出等腰三角形,使问题得到解决.
3.(构造直角三角形法)(2024江西南昌期末)如图,将☉O沿着 弦AB翻折,劣弧恰好经过圆心O.如果弦AB=4 ,那么☉O的半径为(M9103001)(　    ) A.2　　　    B.4　　　    C.2 　　　    D.4 
解析　如图,过点O作OD⊥AB于D,连接OA. ∵OD⊥AB,AB=4 ,∴AD= AB=2 .由折叠得OD= AO.设OD=x,则AO=2x.在Rt△OAD中,AD2+OD2=OA2,∴(2 )2+x2=(2x)2,解得x=2(舍负),∴OA=2x=4,即☉O的半径为4.故选B.
4.(情境题·现实生活)(2024江苏扬州高邮期中)综合实践活动 要求只用一张矩形纸条和刻度尺测量如图1所示的茶碗的碗 口半径.李靓同学所在的学习小组的方法是:如图2,将纸条拉 直紧贴在杯口上,纸条的上下边沿分别与杯口相交于A、B、 C、D四点.若该纸条宽为8 cm,用刻度尺量得AB=6 cm,CD=1 0 cm,则纸杯的半径为　　　    .(结果保留根号)(M9103001)      
解析　如图,过圆心O作MN⊥AB,交AB于N,交CD于M,连接 OD、OB,则MN=8 cm. ∵CD∥AB,∴MN⊥CD,∴DM= CD= ×10=5(cm),∵MN⊥AB,∴BN= AB= ×6=3(cm).
设OM=x cm,则ON=MN-OM=(8-x)cm.∵OM2+MD2=OD2,ON2+BN2=OB2,∴OM2+MD2=ON2+BN2,∴x2+52=(8-x)2+32,∴x=3,∴OM=3 cm,∴OD= =  cm.
通过本课时的学习，需要我们： 1．理解圆的轴对称性及垂径定理的推证过程；能初步应用垂径定理进行计算和证明； 2．利用垂径定理解决相应的数学问题.
3.一条直线满足:①过圆心;②垂直于弦; ③平分弦（不是直径）; ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论（“知二推三”）
1、课本70练习1,22、习题3.1T1