八年级上册3.2 立方根公开课教案设计

这是一份八年级上册3.2 立方根公开课教案设计，共6页。

课题
3.2 立方根
单元
第三单元
学科
数学
年级
八年级
学习
目标
1、了解立方根的概念，会用根号表示一个数的立方根；
2、了解开立方与立方互为逆运算，能用立方运算求一些数的立方根；
3、能用立方根解决一些简单的实际问题.
重点
理解立方根的概念和表示方法
难点
能用立方根解决一些简单的实际问题.
教学过程
教学环节
教师活动
学生活动
设计意图
新知导入
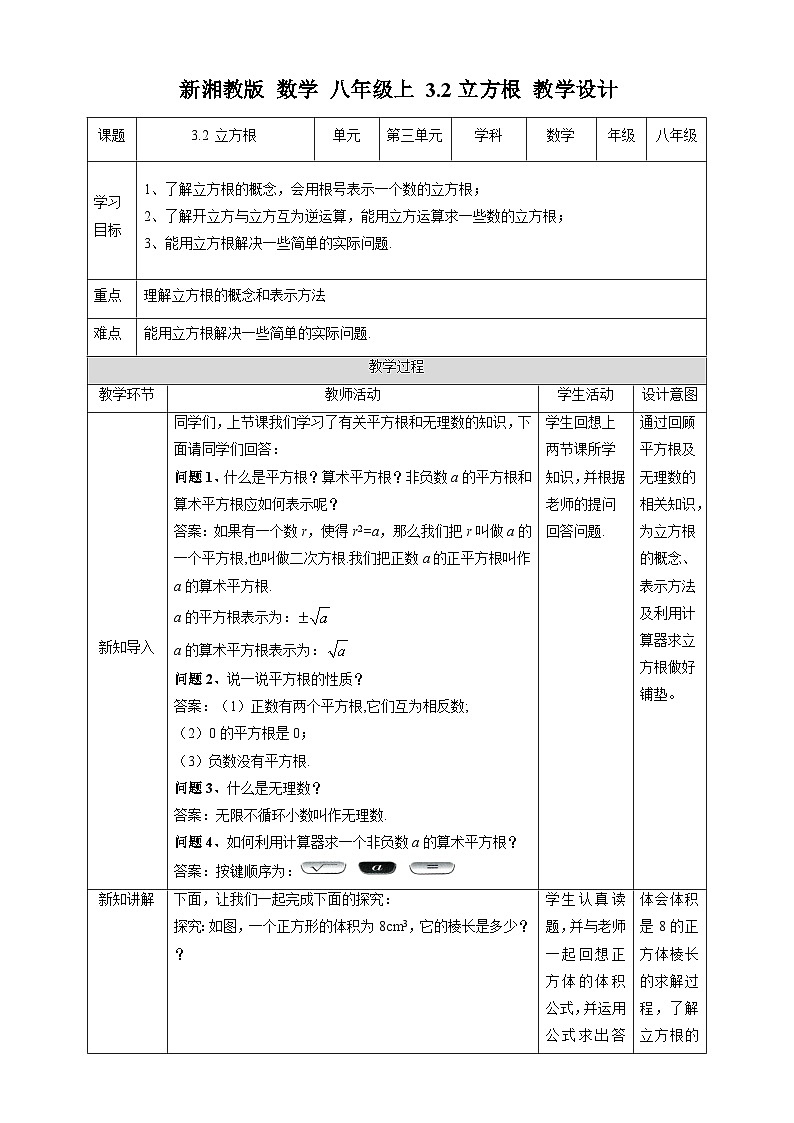
同学们，上节课我们学习了有关平方根和无理数的知识，下面请同学们回答：
问题1、什么是平方根？算术平方根？非负数a的平方根和算术平方根应如何表示呢？
答案：如果有一个数r，使得r2=a，那么我们把r叫做a的一个平方根,也叫做二次方根.我们把正数a的正平方根叫作a的算术平方根.
a的平方根表示为：
a的算术平方根表示为：
问题2、说一说平方根的性质？
答案：（1）正数有两个平方根,它们互为相反数;
（2）0的平方根是0；
（3）负数没有平方根.
问题3、什么是无理数？
答案：无限不循环小数叫作无理数.
问题4、如何利用计算器求一个非负数a的算术平方根？
答案：按键顺序为：
学生回想上两节课所学知识，并根据老师的提问回答问题.
通过回顾平方根及无理数的相关知识，为立方根的概念、表示方法及利用计算器求立方根做好铺垫。
新知讲解
下面，让我们一起完成下面的探究：
探究：如图，一个正方形的体积为8cm3，它的棱长是多少？
？
追问：你还记得正方体的体积与棱长有什么关系吗？
答案：
解：设这个正方体的棱长为xcm，
则x3＝8
∵23＝8
∴x＝2
答：这个正方体的棱长为2cm.
指出：若b3=a，则b是a的一个立方根，即
例如：由于23=8,因此2是8的一个立方根，即
由于（-3）3=-27,因此_____是-27的一个立方根，即
答案：-3；-3
归纳2：求一个数的立方根的运算，叫做开立方.
指出：开立方与立方也互为逆运算，根据这种关系，可以求一个数的立方根.
例1：分别求下列各数的立方根：
解：由于13=1，因此
由于，因此
由于03=0，因此
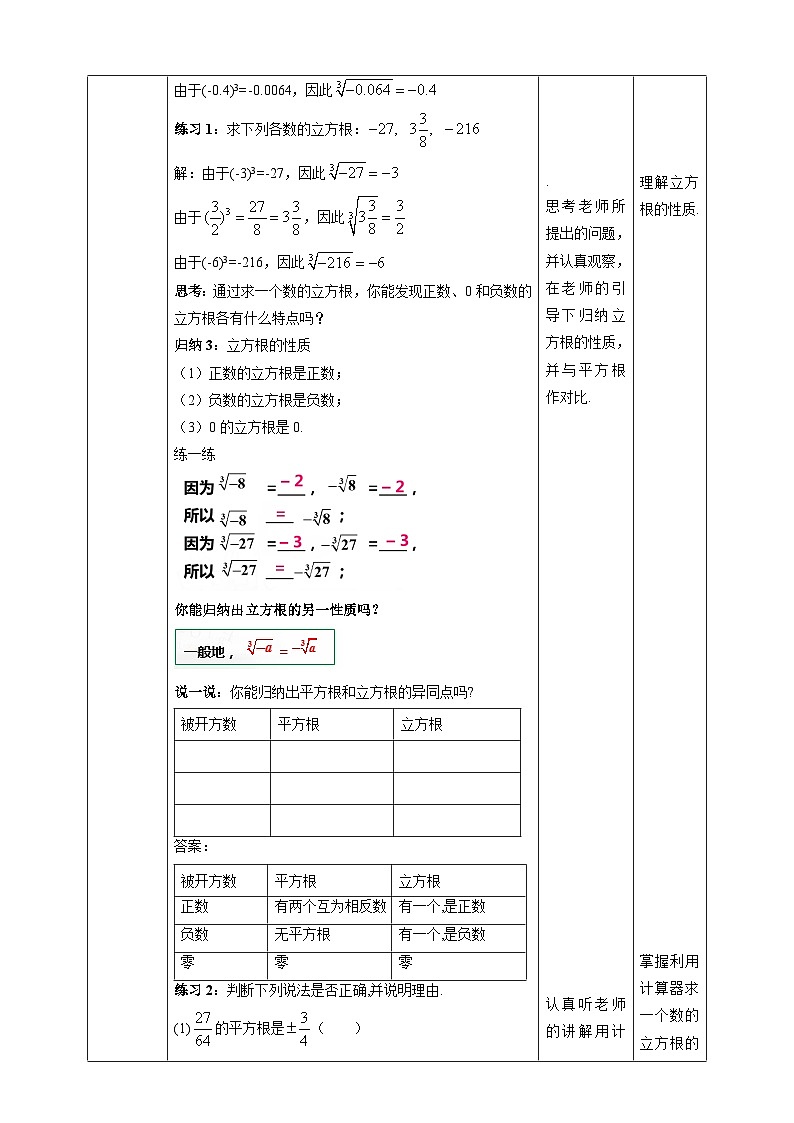
由于(-0.4)3=-0.0064，因此
练习1：求下列各数的立方根：
解：由于(-3)3=-27，因此
由于，因此
由于(-6)3=-216，因此
思考：通过求一个数的立方根，你能发现正数、0和负数的立方根各有什么特点吗？
归纳3：立方根的性质
（1）正数的立方根是正数；
（2）负数的立方根是负数；
（3）0的立方根是0.
练一练
你能归纳出立方根的另一性质吗？
说一说：你能归纳出平方根和立方根的异同点吗?
被开方数
平方根
立方根
答案：
被开方数
平方根
立方根
正数
有两个互为相反数
有一个,是正数
负数
无平方根
有一个,是负数
零
零
零
练习2：判断下列说法是否正确,并说明理由.
(1)的平方根是（ ）
(2)25的平方根是5（ ）
(3)－64没有立方根（ ）
(4)－4的平方根是±2（ ）
(5)0的平方根和立方根都是0（ ）
答案：×；×；×；×；√
追问1：立方根是它本身的数有那些?
答案：0，±1
追问2：算术平方根是它本身的数有那些?
答案：0，1
指出：利用计算器可以求一个数的立方根或它的近似值.
按键顺序为：
其中：是第二功能键
例2：用计算器求下列各数的立方根：
解：（1）依次按键：
显示：7
所以：
（2）依次按键：
显示：-1.1
所以：
例3：用计算器求的近似值（精确到0.001）
解：依次按键：
显示：1.25992105
所以：
指出：实际上，许多有理数的立方根都是无理数，如，…都是无理数.
学生认真读题，并与老师一起回想正方体的体积公式，并运用公式求出答案，然后仔细听老师讲解立方根的相关知识..
学生积极回答老师的提问.
学生认真审题后回答问题，并观察老师的板书后独立书写例题及练习题，然后班内交流
.
思考老师所提出的问题，并认真观察，在老师的引导下归纳立方根的性质，并与平方根作对比.
认真听老师的讲解用计算器求立方根的方法，然后独立完成例题及练习题，最后班内交流，并认真听老师的讲评.
体会体积是8的正方体棱长的求解过程，了解立方根的相关概念..
体会开立方运算
掌握利用立方运算来求一个数的立方根的方法.
理解立方根的性质.
掌握利用计算器求一个数的立方根的方法
课堂练习
下面请同学生独立完成课堂练习.
1.8的立方根是（ ）
A.2 B.±2 C.4 D.±4
答案：A
2.的绝对值是（ ）
A.－27 B.27 C.－3 D.3
答案：D
3.1的平方根是_______；1立方根是_______.
答案：±1，1
4.比较3，4，的大小.
解:∵33＝27，
∴
∵43＝64，
∴
∵
∴
归纳：被开方数越大，对应的立方根也越大.
5.求下列各式的值：
解：
追问：观察算式和结果，你发现了什么呢?
归纳：，
学生自主完成课堂练习，做完之后班级内交流.
借助练习，检测学生的知识掌握程度，同时便于学生巩固知识.
拓展提高
我们一起完成下面的问题：
利用计算器计算，并将计算结果填在表中，你发现了什么规律？
…
…
…
…
答案：0.06；0.6；6；60
规律：被开方数的小数点向右（或向左）移动3位，其立方根的小数点向右（或向左）移动1位.
在师的引导下完成问题.
提高学生对知识的应用能力
课堂总结
在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：
1、什么是立方根？a的立方根如何表示？
答案：如果一个数b，使得b3=a，那么我们把b叫作a的一个立方根，也叫作三次方根. a的立方根记作
2、立方根的性质是什么？
答案：正数的立方根是正数；负数的立方根是负数；0的立方根是0.
3、如何利用计算器求一个a的立方根？
答案：按键顺序为：
跟着老师回忆知识，并记忆本节课的知识.
帮助学生加强记忆知识.
作业布置
基础作业
教材第114页习题3.2A组第1、2、3、4题
能力作业
教材第114页习题3.2B组第5、6题
学生课下独立完成.
检测课上学习效果.
板书设计
课题：3.2 立方根
教师板演区
学生展示区
1、立方根
2、立方根的性质
3、利用计算器求一个数的立方根
借助板书，让学生知道本节课的重点。