新高考数学一轮复习考点精讲练+易错题型第10讲 函数的图像（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习考点精讲练+易错题型第10讲 函数的图像（2份打包，原卷版+解析版），文件包含新高考数学一轮复习考点精讲练+易错题型第10讲函数的图像原卷版doc、新高考数学一轮复习考点精讲练+易错题型第10讲函数的图像解析版doc等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。

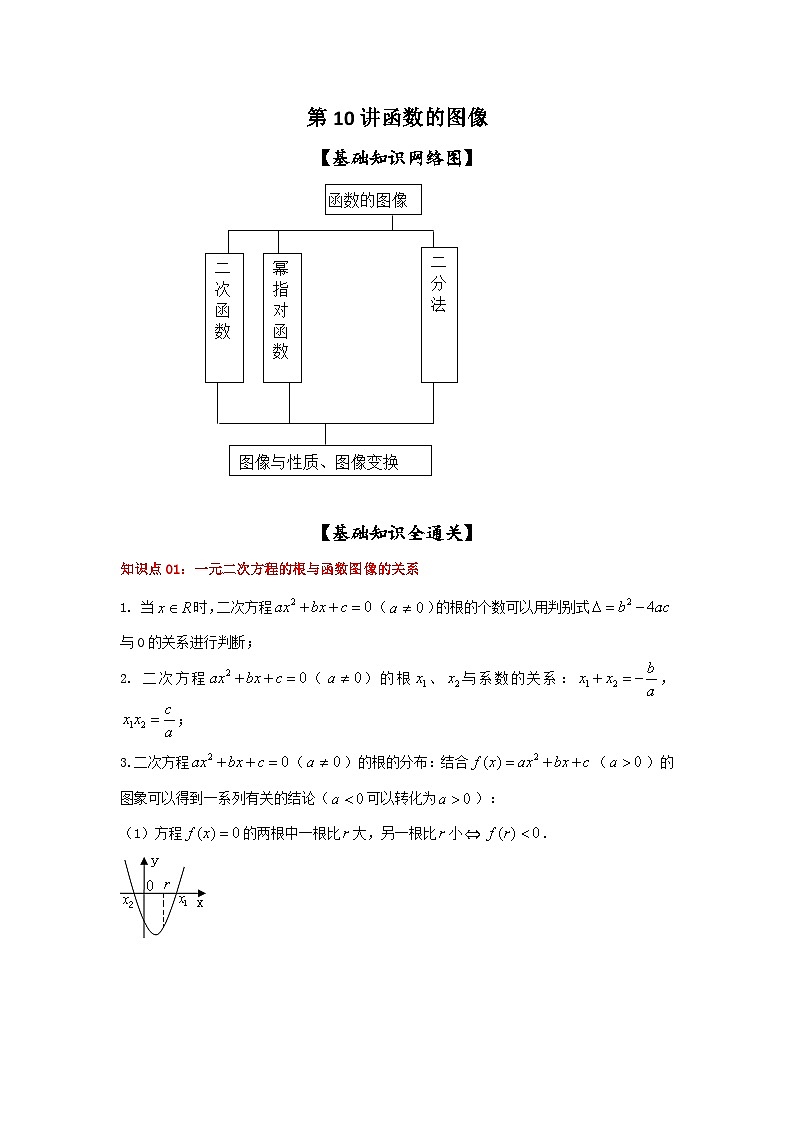
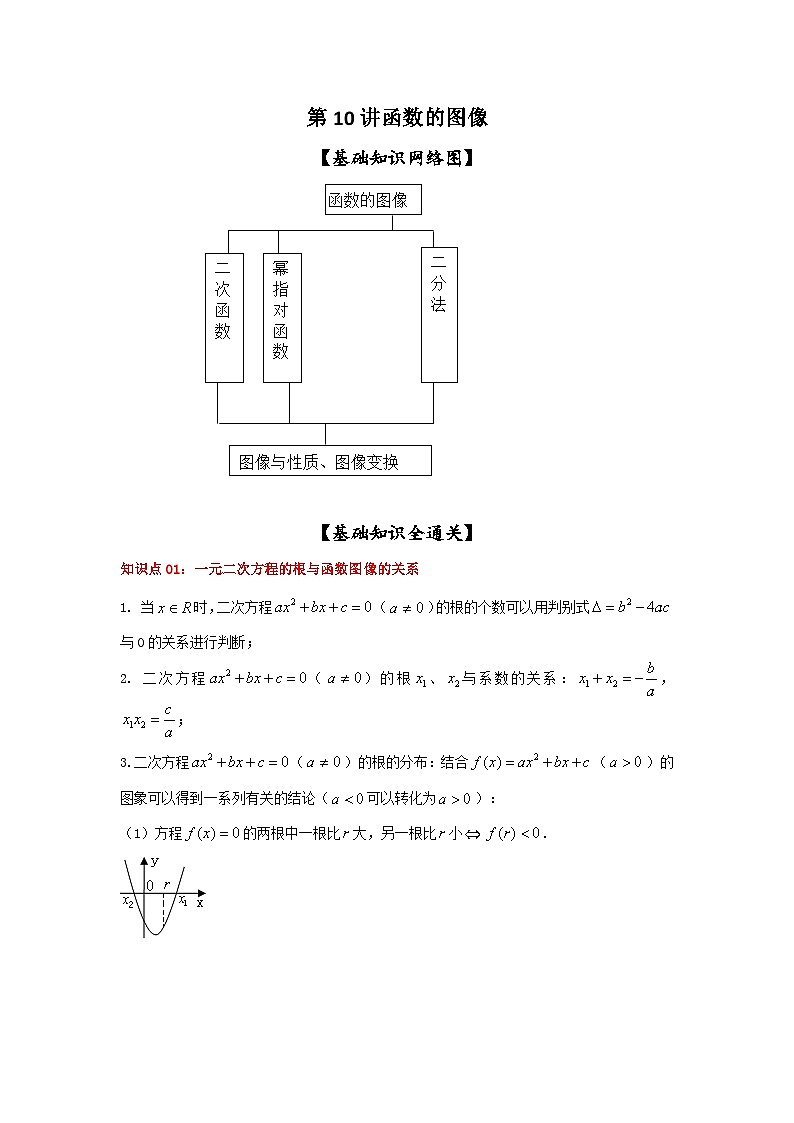
函数的图像
图像与性质、图像变换
幂指对函数
二分法
二次函数
【基础知识全通关】
知识点01：一元二次方程的根与函数图像的关系
1. 当时，二次方程（）的根的个数可以用判别式与0的关系进行判断；
2. 二次方程（）的根、与系数的关系：，；
3.二次方程（）的根的分布：结合（）的图象可以得到一系列有关的结论（可以转化为）：
（1）方程的两根中一根比大，另一根比小.
（2）二次方程的两根都大于
（3）二次方程在区间内有两根
（4）二次方程在区间内只有一根，或而另一根在内，或而另一根在内.
（5）方程的一根比小且一根比大（）
知识点02：零点
1. 函数的零点
(1) 一般地，如果函数在实数a处的值为0，即，则a叫做这个函数的零点．
(2) 对于任意函数，只要它的图象是连续不间断的，其函数的零点具下列性质：
① 当它通过零点（不是偶次零点）时函数值符号改变；
② 相邻两个零点之间的所有的函数值保持符号不变。
(3)函数零点的性质是研究方程根的分布问题的基础，是通过对二次函数的零点的研究而推出的．是由特殊到一般的思想方法。
2.二分法
(1) 已知函数在区间[a，b]上连续的，且，通过不断地把函数的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，从而得到零点的近似值的方法，叫做二分法。
(2)二分法定义的基础，是函数零点的性质；二分法定义本身给出了求函数零点近似值的步骤．只要按步就班地做下去，就能求出给定精确度的函数零点．
（3）二分法求函数零点的近似值的步骤，渗透了算法思想与程序化意识．此步骤本身就是一个解题程序。这种程序化思想在计算机上得到了广泛的应用．
知识点03：函数模型
常用的几类函数模型
(1)一次函数模型：；
(2)反比例函数模型：；
(3)二次函数模型：；
(4)指数函数模型：；
(5)对数函数模型：；
(6)幂函数模型：。
知识点04：图象变换
（一） 函数图象
1.作图方法：
以解析式表示的函数作图象的方法有两种，即列表描点法和图象变换法，掌握这两种方法是本节的重点．运用描点法作图象应避免描点前的盲目性，也应避免盲目地连点成线．要把表列在关键处，要把线连在恰当处．这就要求对所要画图象的存在范围、大致特征、变化趋势等作一个大概的研究．而这个研究要借助于函数性质、方程、不等式等理论和手段，是一个难点．用图象变换法作函数图象要确定以哪一种函数的图象为基础进行变换，以及确定怎样的变换．这也是个难点．
2.作函数图象的步骤：
①确定函数的定义域；②化简函数的解析式；
③讨论函数的性质即单调性、奇偶性、周期性、最值（甚至变化趋势）、特殊点（如：零点、极值点、与轴的交点）；
④描点连线，画出函数的图象。
（二） 图象变换
图象变换包括图像的平移变换、伸缩变换、对称变换、翻折变换等。
（1）平移变换（左加右减，上加下减）
把函数的图像向左平移个单位，得到函数的图像，
把函数的图像向右平移个单位，得到函数的图像，
把函数的图像向上平移个单位，得到函数的图像，
把函数的图像向下平移个单位，得到函数的图像。
（2）伸缩变换
①把函数图象的纵坐标不变，横坐标伸长到原来的倍得 (0<<1)
②把函数图象的纵坐标不变，横坐标缩短到原来的倍得 (>1)
③把函数图象的横坐标不变，纵坐标伸长到原来的倍得 (>1)
④把函数图象的横坐标不变，纵坐标缩短到原来的倍得 (0<<1)
（3）对称变换：
①函数和函数的图像关于轴对称
函数和函数的图像关于轴对称
函数和函数的图像关于原点对称
函数和函数的图像关于直线对称
简单地记为：轴对称要变，轴对称要变，原点对称都要变。
②对于函数(),恒成立,则函数的对称轴是
（4）翻折变换：
①把函数y=f(x)图像上方部分保持不变，下方的图像对称翻折到轴上方，得到函数的图像；
②保留轴右边的图像，擦去左边的图像，再把右边的图像对称翻折到左边，得到函数的图像。
【考点研习一点通】
考点01：图象变换
【典例1】1．由函数的图象，通过怎样的图象变换，可以作出的图象？
【解析】∵，
∴要得到的图象，需要把的图象经过以下的变换才能得到：
即.
【总结】作函数图象的基本方法有两种：
(1)描点法 ；
(2)图象变换法：利用基本初等函数变换作图，其中掌握好(1)平移变换，(2) 对称变换， (3) 伸缩变换。
【典例2】（2022·浙江绍兴市·高三三模）函数的图象可能是（ ）
A．B．
C．D．
【答案】B
【解析】
根据，得到的图象关于对称，再利用特殊值判断.
【详解】
因为，
所以的图象关于对称，
又，
故选：B
【典例3】分别画出下列函数的图象：
【答案】见解析
【解析】 (1)首先作出y＝lg x的图象C1，然后将C1向右平移1个单位，得到y＝lg(x－1)的图象C2，再把C2在x轴下方的图象作关于x轴对称的图象，即为所求图象C3：y＝|lg(x－1)|.如图1所示(实线部分).
(2)y＝2x＋1－1的图象可由y＝2x的图象向左平移1个单位，得y＝2x＋1的图象，再向下平移一个单位得到，如图2所示.
(3) 第一步作y＝lgx的图像．
第二步将y＝lgx的图像沿y轴对折后与原图像，同为y＝lg|x|的图像．
第三步将y＝lg|x|的图像向右平移一个单位，得y＝lg|x－1|的图像
第四步将y＝lg|x－1|的图像在x轴下方部分沿x轴向上翻折，得的图像，如图3．
【规律方法】
1．平移变换
当m>0时，y＝f(x－m)的图象可以由y＝f(x)的图象向右平移m个单位得到；y＝f(x＋m)的图象可以由y＝f(x)的图象向左平移m个单位得到；y＝f(x)＋m的图象可以由y＝f(x)的图象向上平移m个单位得到；y＝f(x)－m的图象可以由y＝f(x)的图象向下平移m个单位得到．
2．对称(翻折)变换
y＝f(|x|)的图象可以将y＝f(x)的图象位于y轴右侧和y轴上的部分不变，原y轴左侧部分去掉，画出y轴右侧部分关于y轴对称的图形而得到．y＝|f(x)|的图象可将y＝f(x)的图象位于y轴上方的部分不变，而将位于y轴下方的部分翻折到y轴上方得到．y＝－f(x)的图象可将y＝f(x)的图象关于x轴对称而得到．y＝f(－x)的图象可由y＝f(x)的图象关于y轴对称得到．
考点02：图象的识别
【典例4】（2022·四川高三三模（理））函数及，则及的图象可能为（ ）
A．B．
C．D．
【答案】B
【解析】
讨论、确定的单调性和定义域、在y轴上的截距，再讨论、，结合的单调性，即可确定函数的可能图象.
【详解】
当时，单调递减，单调递减，所以单调递增且定义域为，此时与y轴的截距在上，排除C.
当时，单调递减，单调递增，所以单调递减且定义域为，此时与y轴的截距在上.
∴当时，单调递增；当时，单调递减，故只有B符合要求.
故选：B.
【典例5】（2019·全国高考真题（理））函数在的图像大致为
A．B．
C．D．
【答案】B
【解析】
设，则，所以是奇函数，图象关于原点成中心对称，排除选项C．又排除选项D；，排除选项A，故选B．
【典例6】（2022·云南高三三模（理））函数的大致图象为（ ）
A．B．
C．D．
【答案】B
【解析】
判断图像类问题，首先求定义域，其次判断函数的奇偶性；再次通过图像或函数表达式找特殊值代入求值，时，即，此时只能是；也可通过单调性来判断图像.主要是通过排除法得解.
【详解】
函数的定义域为，
因为，
并且，
所以函数为奇函数，其图象关于原点对称，可排除；
当时，即，此时只能是，
而的根是，可排除.
故选:
【总结提升】
识图的三种常用方法
1．抓住函数的性质，定性分析：
（1）由函数的定义域，判断图象的左、右位置，由函数的值域，判断图象的上、下位置；
（2）由函数的单调性，判断图象的变化趋势；
（3）由函数的奇偶性，判断图象的对称性；
（4）由函数的周期性，判断图象的循环往复．
2．抓住函数的特征，定量计算：
从函数的特征点，利用特征点、特殊值的计算分析解决问题．
3．根据实际背景、图形判断函数图象的方法：
(1)根据题目所给条件确定函数解析式，从而判断函数图象(定量分析)；
(2)根据自变量取不同值时函数值的变化、增减速度等判断函数图象(定性分析)．
考点03：从图象到解析式
【典例7】（2022·河南高三月考（理））已知函数，，则下列图象对应的函数可能为（ ）
A．B．
C．D．
【答案】D
【解析】
A.当时，，不符合题意；
B.其图象不关于轴对称，不符合题意；
C.其图象不关于轴对称，不符合题意；
D.其图象关于轴对称，当时，，符合题意.
【详解】
A.，当时，，不符合题意；
B.，其图象不关于轴对称，不符合题意；
C.，其图象不关于轴对称，不符合题意；
D.，其图象关于轴对称，当时，，符合题意.
故选：D.
【典例8】（2022·四川达州市·高三二模（理））已知函数与的部分图象如图1，则图2可能是下列哪个函数的部分图象（ ）
A．B．C．D．
【答案】B
【解析】
根据奇函数、偶函数的图象特征，结合奇偶函数的性质逐一判断即可.
【详解】
由图1可知：函数关于纵轴对称，因此该函数是偶函数，即.
函数的图象关于原点对称，因此该函数是奇函数，即.
由图2可知：该函数关于原点对称，因此该函数是奇函数.
A：设，因为，
所以是偶函数，不符合题意；
B：设，因为，
所以是奇函数，符合题意；
C：设，因为，
所以是偶函数，不符合题意；
D：由图1可知：，因为函数在时没有意义，故不符合题意，
故选：B
【规律方法】
根据图象找解析式，一般先找差异，再验证.
考点04：用图
【典例9】（山东省春季真题））奇函数的局部图像如图所示，则（ ）
A. B.
C. D.
【答案】A
【解析】因为奇函数，所以,
因为>0>，所以,即，
选A.
【典例10】（2022·吉林白山市·高三三模（理））如图，函数的图象由一条射线和抛物线的一部分构成，的零点为，若不等式对恒成立，则a的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】
由条件可知，的图象是由向左平移个单位长度得到，再利用数形结合，分析图象的临界条件，得到的取值范围.
【详解】
当时，，图象过点和，即，
解得：，，即，
当时，设抛物线，代入点得，，即，
所以 ，
的图象是由向左平移个单位长度得到，因为，对恒成立，所以的图象恒在的上方，当两图象如图所示，相切时，
抛物线，，
与直线相切，即，解得：，，
切点代入得，
得，所以，解得：或.
故选：A
【典例11】（2022·北京高考模拟（理））已知函数f（x）=2x（x＜0）与g（x）=ln（x+a）的图象上存在关于y轴对称的点，则a的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】
在同一直角坐标系中作出函数f（x）=2x（x＜0）与g（x）=ln（x+a）的图象，
当y=lnx向左平移a（a＞0）个单位长度，恰好过（0，1）时，函数f（x）与g（x）就不存在关于y轴对称的点，所以0＜a＜e，
当y=lnx向右平移（a＜0）个单位长度，函数f（x）与g（x）总存在关于y轴对称的点，
当a=0时，显然满足题意，综上：a＜e，
故选：B．
【典例12】（2021·全国高三其他（文））已知函数在区间的值域为，则（ ）
A．2B．4C．6D．8
【答案】C
【解析】
在上为奇函数，图象关于原点对称，是将上述函数图象向右平移2个单位，并向上平移3个单位得到，所以图象关于对称，则，故选.
【考点易错】
易错01：图象变换
1、由函数的图象，通过怎样的图象变换，可以作出的图象？
【解析】
∵，
∴要得到的图象，需要把的图象经过以下的变换才能得到：
即.
【总结】作函数图象的基本方法有两种：
(1)描点法 ；
(2)图象变换法：利用基本初等函数变换作图，其中掌握好(1)平移变换，(2) 对称变换， (3) 伸缩变换。
【变式1-1】写出下列函数作图过程，然后画出下列函数图像的草图.
（1） （2） （3） （4）
【解析】（1）
先作出函数的图像，
再把函数的图像向右平移一个单位得到函数的图像，
最后把函数的图像向上平移2个单位，
得到函数的图像。
（2） 然后作出函数的图像。
（3）首先作出函数的图像，
再把函数的图像轴上方保持不变，
把轴下方的图像对称地翻折到轴上方，
即得函数的图像。
（4）首先作出函数的图像，
然后把的图像轴右边的保持不变，去掉轴左边的图像，
再把轴右边的图像对称地翻折到轴左边，即得函数的图像，
最后把函数的图像向左平移一个单位，
得到函数的图像。
【总结】
作函数图像的基本方法有两种：
(1)描点法 ；
(2)图像变换法：利用基本初等函数变换作图，其中掌握好(1)平移变换；(2) 对称变换；(3) 伸缩变换。
易错02：一元二次方程的根的分布
2．已知函数的一个零点比1大，一个零点比l小。求实数的取值范围．
【解析】
方法一：设方程的两根分别为、（）
则 即
由韦达定理得：
即，解得：
方法二：函数的大致图象如图：
则 即
解得：
【总结】
1. 这类题为方程的实根分布问题，解决此类问题一定要注意结合图象，从判别式、韦达定理、对称轴、端点函数值的大小、开口方向等方面去考虑使结论成立的所有条件。函数与方程联系密切，可把函数问题转化为方程问题解决，也可用数形结合法。
2. 函数y=ax2+bx+c, 当a≠0时，才是二次函数，具体问题时，切忌忽略讨论a=0的情况。
3．三个”二”次的关系是高考考查的重中之重，把二次方程和二次不等式的问题从二次函数的观点出发运用数形结合思想分析处理是高考应考必须落实的基本思路。
【变式2-1】已知方程至少有一正根，求实数的取值范围.
【答案】从二次函数的观点出发，结合函数图像与x轴交点的位置解决问题并对进行分类讨论。
令，
则函数的图像与轴的交点至少有一个在原点的右侧，
（1）若，则与x轴交点，符合题意。
（2）若，∵，即函数的图像一定过点，有
①当时，的图像开口向上，只有下图所示情形符合题意，
∴即,解得.
②当时，的图像开口向下，必然有一个交点在原点右侧，符合题意.
综上可得
易错03：零点的判定
3. 求方程的解的个数．
【解析】作出函数和的图象，
且时，，，有（如图）
由图象可以知道：函数和的图象的交点的个数为3，
即方程的解的个数为3.
【总结】
1.本题在求解的过程中，只需作出反映函数性状的“大致”图象，结合函数的单调区间便可解决本问题，只要得出极大值为正，极小值为负，便可立即得到原方程有3个根．
2.把方程问题转化为函数问题，将方程和函数紧密联系起来，利用数形结合思想解决问题比较方便。通过计算作方程所对应函数的函数值表格或作出函数的图象，用函数值的变化情况分析零点所在的区间，然后再利用单调性确定个数。
3. 对于超越方程的根，无法用代数的方法求得它的具体的解，只能把方程问题转化为函问题确定它的解的个数.例如：，，等
易错04：综合应用
4. 已知点在函数的图象上运动 ，其对应点在函数的图象上运动，
（1）求的解析式；
（2）问：是否存在实数,()，使得函数在区间上的值域为.
【解析】
（1）设的图象上的点,据题意有：即，
∵点在函数的图象上
∴， ∴.
（2）由（1）知：， ∴的图象的对称轴：，
又, 则有：
①当时，在区间上单调递增，有，
即，解得，∴ , .
②当时，易知，所以,显然不合题意.
③当时，，根据计算易知不合题意.
∴ 综上，, .
另解：∵,
∴ ，即, ∴,
∵对称轴：， ∴在区间上单调递增，则有，
即，解得，
∴ , .
【总结】这是一个求轨迹方程与二次函数的综合问题。求轨迹实质是相关点法解决的，而二次函数问题是属于给定二次函数，而取值的区间是一个动区间的问题，其值域与二次函数图象变化趋势相关，即要抓住二次函数单调性改变的分界线即对称轴与的相对位置展开讨论，并且不重不漏。而另解中应用了二次函数的最值，从而确定了与对称轴之间的位置，使问题的解法一下子就简化了。
【变式4-1】已知函数(,,)是奇函数，当时，有最小值2，其中且.
(1)试求函数的解析式；
(2)问函数的图象上是否存在关于点对称的两点，若存在，求出点的坐标；若不存在，说明理由
【答案】
(1)∵是奇函数，∴,即，∴,
∵, ,∴当时，，
当且仅当，即时等号成立，
∴于是,∴,
由得，即，∴,解得，
又,∴,, ∴.
(2)设存在一点在的图象上，
并且关于点的对称点也在的图象上，
则，消去得,解得：.
代入方程解得：或，
∴的图象上存在两点,关于点对称.
【巩固提升】
1．（2021·湖南株洲市·高三二模）若函数的大致图象如图所示，则（ ）
A．B．
C．D．
【答案】B
【解析】
令得到，再根据函数图象与x轴的交点和函数的单调性判断.
【详解】
令得，即，
解得，
由图象知，
当时，，当时，，故排除AD，
当时，易知是减函数，
当时，，，故排除C
故选：B
2．（2022·浙江高三专题练习）函数的图象是（ ）
A．B．
C．D．
【答案】C
【解析】
将函数的图象进行变换可得出函数的图象，由此可得出合适的选项.
【详解】
将函数的图象先向右平移个单位长度，可得到函数的图象，
再将所得函数图象位于轴下方的图象关于轴翻折，位于轴上方图象不变，可得到函数的图象.
故合乎条件的图象为选项C中的图象.
故选：C.
3．（2021·吉林长春市·东北师大附中高三其他模拟（理））函数的图象大致为（ ）
A．B．
C．D．
【答案】C
【解析】
求出函数的定义域，利用导数分析函数的单调性，结合排除法可得出合适的选项.
【详解】
对于函数，则有，解得且，
所以，函数的定义域为，排除AB选项；
对函数求导得.
当或时，；当时，.
所以，函数的单调递减区间为、，单调递增区间为，
当时，，当时，，排除D选项.
故选：C.
4．（2022·全国高三专题练习（文））函数的图象大致是（ ）．
A．B．
C．D．
【答案】B
【解析】
由和可排除ACD，从而得到选项.
【详解】
由，可排除AD；
由，可排除C；
故选：B.
5．（2021·天津高三三模）意大利画家列奥纳多·达·芬奇的画作《抱银鼠的女子》（如图所示）中，女士颈部的黑色珍珠项链与她怀中的白貂形成对比.光线和阴影衬托出人物的优雅和柔美.达·芬奇提出：固定项链的两端，使其在重力的作用下自然下垂，形成的曲线是什么？这就是著名的“悬链线问题”.后人研究得出，悬链线并不是抛物线，而是与解析式为的“双曲余弦函数”相关.下列选项为“双曲余弦函数”图象的是（ ）
A．B．
C．D．
【答案】C
【解析】
分析函数的奇偶性与最小值，由此可得出合适的选项.
【详解】
令，则该函数的定义域为，，
所以，函数为偶函数，排除B选项.
由基本不等式可得，当且仅当时，等号成立，
所以，函数的最小值为，排除AD选项.
故选：C.
6．（2022·宁夏吴忠市·高三其他模拟（文））已知函数，则（ ）．
A．的图象关于直线对称B．的图象关于点对称
C．在上单调递增D．在上单调递减
【答案】A
【解析】
先求出函数的定义域.
A：根据函数图象关于直线对称的性质进行判断即可；
B：根据函数图象关于点对称的性质进行判断即可；
C：根据对数的运算性质，结合对数型函数的单调性进行判断即可；
D：结合C的分析进行判断即可.
【详解】
的定义域为，
A：因为，
所以函数的图象关于对称，因此本选项正确；
B：由A知，所以的图象不关于点对称，因此本选项不正确；
C：
函数在时，单调递增，
在时，单调递减，因此函数在时单调递增，在时单调递减，故本选项不正确；
D：由C的分析可知本选项不正确，
故选：A
7.（2019·北京高三高考模拟（文））当x∈[0，1]时，下列关于函数y=的图象与的图象交点个数说法正确的是（ ）
A．当时，有两个交点B．当时，没有交点
C．当时，有且只有一个交点D．当时，有两个交点
【答案】B
【解析】
设f（x）=，g（x）= ，其中x∈[0，1]
A．若m=0，则与在[0，1]上只有一个交点，故A错误．
B．当m∈（1，2）时，
即当m∈（1，2]时，函数y=的图象与的图象在x∈[0，1]无交点，故B正确，
C．当m∈（2，3]时，，
当时，此时无交点，即C不一定正确．
D．当m∈（3，+∞）时，g（0）=＞1，此时f（1）＞g（1），此时两个函数图象只有一个交点，故D错误，
故选：B．
8．（2022·浙江高三专题练习）已知函数f(x)＝则函数y＝f(1－x)的大致图象是（ ）
A．B．
C．D．
【答案】D
【解析】
由得到的解析式，根据函数的特殊点和正负判断即可.
【详解】
因为函数，
所以函数，
当x＝0时，y＝f(1)＝3，即y＝f(1－x)的图象过点(0，3)，排除A；
当x＝－2时，y＝f(3)＝－1，即y＝f(1－x)的图象过点(－2，－1)，排除B；
当时，，排除C，
故选：D．
9.（2019年高考全国Ⅲ卷理）函数在的图像大致为（ ）
A．B．
C．D．
【答案】B
【解析】设，则，所以是奇函数，图象关于原点成中心对称，排除选项C．
又排除选项D；
，排除选项A，
故选B．
10.（2019年高考全国Ⅱ卷理）设函数的定义域为R，满足，且当时，．若对任意，都有，则m的取值范围是
A．B．
C． D．
【答案】B
【解析】∵，．
∵时，；
∴时，，；
∴时，，，
如图：
当时，由解得，，
若对任意，都有，则.
则m的取值范围是.
故选B.
11.（2018·全国高考真题（文））设函数，则满足的x的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】
分析：首先根据题中所给的函数解析式，将函数图像画出来，从图中可以发现若有成立，一定会有，从而求得结果.
详解：将函数的图像画出来，观察图像可知会有，解得，所以满足的x的取值范围是，故选D.
12.对、，记，函数．
（1）求，．
（2）写出函数的解析式，并作出图像．
（3）若关于的方程有且仅有个不等的解，求实数的取值范围．（只需写出结论）
【答案】见解析．
【解析】解：（1）∵，函数，
∴，．
（2）
（3）或．
13．（2021·全国高一课时练习）函数和的图象，如图所示．设两函数的图象交于点，，且．
（1）请指出示意图中曲线，分别对应哪一个函数；
（2）结合函数图象，比较，，，的大小．
【答案】（1）对应的函数为，对应的函数为；（2）．
【解析】
（1）根据图象可得结果；
（2）通过计算可知，再结合题中的图象和在上的单调性，可比较，，，的大小.
【详解】
（1）由图可知，的图象过原点，所以对应的函数为，对应的函数为
（2）因为，，，，，，，，所以，，，
所以，所以
从题中图象上知，当时，；当时，，且在上是增函数，所以．
14．（2021·全国高一单元测试）函数和的图象如图所示，设两函数的图象交于点，，且．
（1）请指出图中曲线，分别对应的函数；
（2）结合函数图象，比较，，，的大小．
【答案】（1）对应的函数为，对应的函数为；（2）．
【解析】
（1）根据指数函数和一次函数的函数性质解题；（2）结合函数的单调性及增长快慢进行比较.
【详解】
（1）对应的函数为，对应的函数为．
（2），，
，
又，，
，；
，，
，
又，，
，．
当时，，
．
．