



所属成套资源:新高考数学一轮复习考点精讲练+易错题型 (2份打包,原卷版+解析版)
- 新高考数学一轮复习考点精讲练+易错题型第25讲 三角函数的图像与性质(2份打包,原卷版+解析版) 试卷 0 次下载
- 新高考数学一轮复习考点精讲练+易错题型第26讲 Y=sin(wx+b)的图像与性质(2份打包,原卷版+解析版) 试卷 0 次下载
- 新高考数学一轮复习考点精讲练+易错题型第28讲 平面向量的概念与线性运算(2份打包,原卷版+解析版) 试卷 0 次下载
- 新高考数学一轮复习考点精讲练+易错题型第29讲 平面向量的基本定理与坐标运算(2份打包,原卷版+解析版) 试卷 0 次下载
- 新高考数学一轮复习考点精讲练+易错题型第30讲 平面向量的数量积(2份打包,原卷版+解析版) 试卷 0 次下载
新高考数学一轮复习考点精讲练+易错题型第27讲 正弦定理、余弦定理及应用(2份打包,原卷版+解析版)
展开
这是一份新高考数学一轮复习考点精讲练+易错题型第27讲 正弦定理、余弦定理及应用(2份打包,原卷版+解析版),文件包含新高考数学一轮复习考点精讲练+易错题型第27讲正弦定理余弦定理及应用原卷版doc、新高考数学一轮复习考点精讲练+易错题型第27讲正弦定理余弦定理及应用解析版doc等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
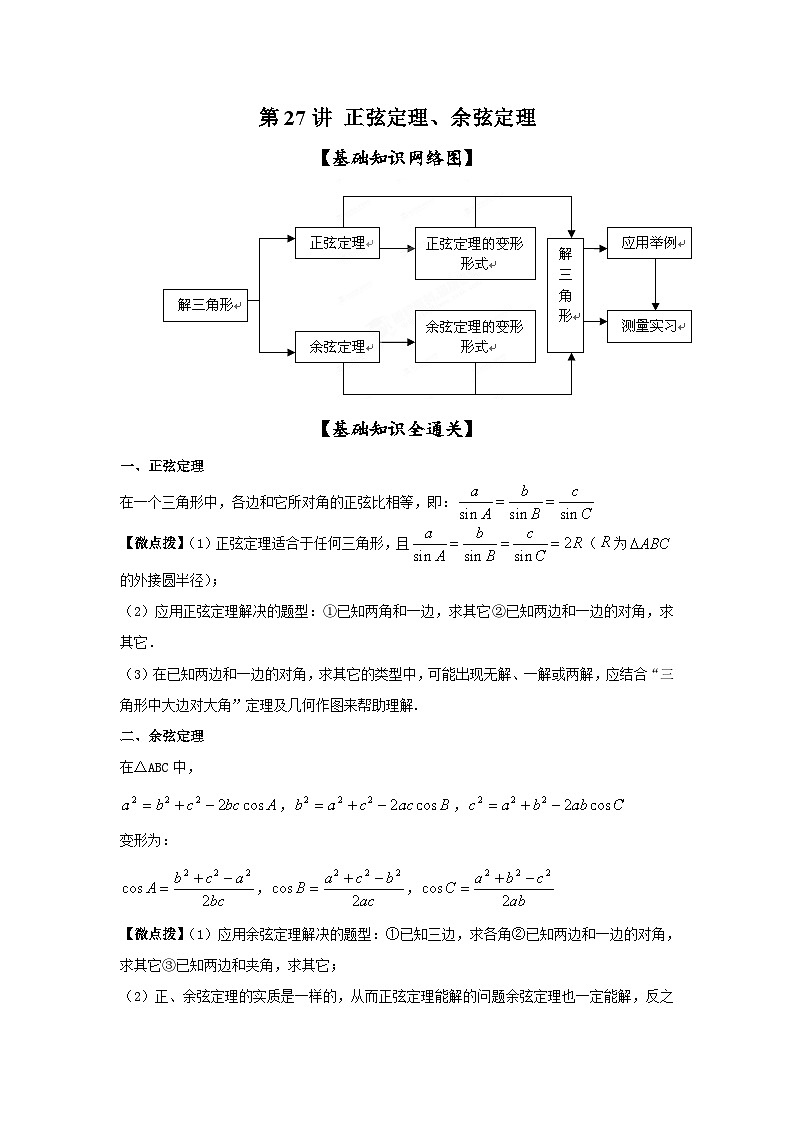
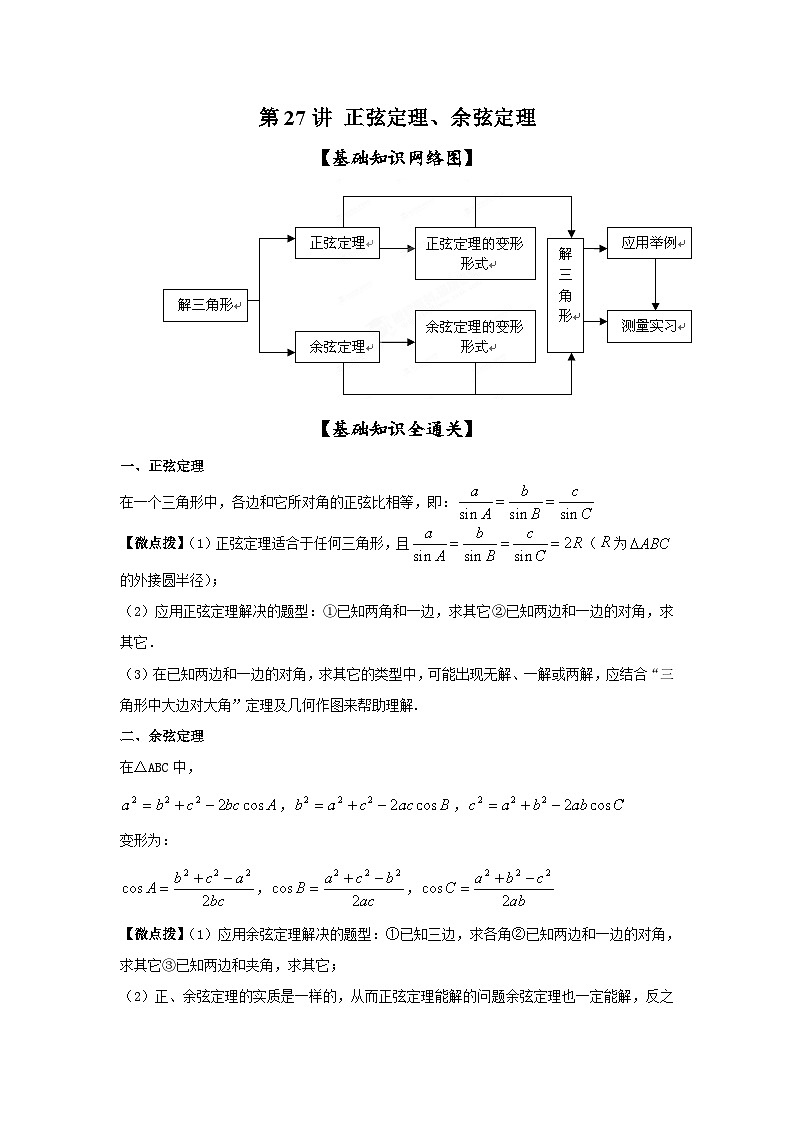
【基础知识全通关】
一、正弦定理
在一个三角形中,各边和它所对角的正弦比相等,即: SKIPIF 1 < 0
【微点拨】(1)正弦定理适合于任何三角形,且 SKIPIF 1 < 0 ( SKIPIF 1 < 0 为 SKIPIF 1 < 0 的外接圆半径);
(2)应用正弦定理解决的题型:①已知两角和一边,求其它②已知两边和一边的对角,求其它.
(3)在已知两边和一边的对角,求其它的类型中,可能出现无解、一解或两解,应结合“三角形中大边对大角”定理及几何作图来帮助理解.
二、余弦定理
在△ABC中,
SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0
变形为:
SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0
【微点拨】(1)应用余弦定理解决的题型:①已知三边,求各角②已知两边和一边的对角,求其它 = 3 \* GB3 ③已知两边和夹角,求其它;
(2)正、余弦定理的实质是一样的,从而正弦定理能解的问题余弦定理也一定能解,反之亦然;只是方便程度有别;
(3)正、余弦定理可以结合使用.
三、三角形的面积公式
(1) SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0 为 SKIPIF 1 < 0 边上的高
(2) SKIPIF 1 < 0
(3) SKIPIF 1 < 0 ,其中 SKIPIF 1 < 0
四、三角形形状的判定方法
设△ABC的三边为a、b、c,对应的三个角为A、B、C,
解斜三角形的主要依据是:
(1)角与角关系:由于A+B+C = π,所以sin(A+B)=sinC;cs(A+B)=-csC;tan(A+B)=-tanC; SKIPIF 1 < 0 ;
(2)边与边关系:a + b > c,b + c > a,c + a > b,a-b < c,b-c < a,c-a > b;
(3)边与角关系:正弦定理、余弦定理
常用两种途径:
(1)由正余弦定理将边转化为角;
(2)由正余弦定理将角转化为边.
【微点拨】 = 1 \* GB3 ①化简中将三角形内角和、三角同角基本关系式、诱导公式、两角和与差的三角公式等综合结合起来. = 2 \* GB3 ②在△ABC中,熟记并会证明:∠A,∠B,∠C成等差数列的充分必要条件是∠B=60°;△ABC是正三角形的充分必要条件是∠A,∠B,∠C成等差数列且a,b,c成等比数列.
五、解三角形应用的分类
(1)距离问题:一点可到达另一点不可到达;两点都不可到达;
(2)高度问题(最后都转化为解直角三角形);
(3)角度问题;
(4)面积问题.
【考点研习一点通】
考点01运用正余弦定理解三角形
例1、在 SKIPIF 1 < 0 中,内角 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 所对的边分别为 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 .已知 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 .
(1)求 SKIPIF 1 < 0 , SKIPIF 1 < 0 的值:
(2)求 SKIPIF 1 < 0 的值.
【答案】(1) SKIPIF 1 < 0 , SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 .
【解析】
(1)由 SKIPIF 1 < 0 ,得 SKIPIF 1 < 0 ,
因为在 SKIPIF 1 < 0 中, SKIPIF 1 < 0 ,得 SKIPIF 1 < 0 ,
由余弦定理 SKIPIF 1 < 0 ,得 SKIPIF 1 < 0 ,
因为 SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 ,
解得 SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 .
(2)由 SKIPIF 1 < 0 ,得 SKIPIF 1 < 0
由正弦定理得 SKIPIF 1 < 0 .
方法总结:本题考查正弦定理、余弦定理的公式.在解三角形时,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.考查基本运算能力和转化与化归思想.
【变式1-1】在△ABC中,内角A,B,C的对边分别为 SKIPIF 1 < 0 ,若 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ______.
【答案】4
【解析】
∵ SKIPIF 1 < 0 ,
∴由正弦定理得 SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
又 SKIPIF 1 < 0 ,
∴由余弦定理得 SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 ,
∵ SKIPIF 1 < 0 为 SKIPIF 1 < 0 的内角,∴ SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 ,
∴ SKIPIF 1 < 0 ,
故答案为:4.
【变式1-2】在 SKIPIF 1 < 0 中,若 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 =( )
A.1B.2 C.3D.4
【答案】A
【解析】
余弦定理 SKIPIF 1 < 0 将各值代入
得 SKIPIF 1 < 0
解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 (舍去)选A.
考点02利用正余弦定理判定三角形形状
例2、△ABC中,内角A,B,C所对的边分别为a,b,c,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)若sinB+sinC=1,试判断△ABC的形状.
【解析】 (1)由已知,根据正弦定理得:2a2=(2b+c)b+(2c+b)c,即a2=b2+c2+bc,由余弦定理得:a2=b2+c2-2bccsA,故csA=-eq \f(1,2),A=120°.
(2)由(1)得:sin2A=sin2B+sin2C+sinBsinC,∵A=120°,∴eq \f(3,4)=sin2B+sin2C+sinBsinC,与sinB+sinC=1联立方程组解得:sinB=sinC=eq \f(1,2),∵0°<B<60°,0°<C<60°,故B=C=30°,∴△ABC是等腰钝角三角形.
【变式】(1)设△ABC的内角A,B,C所对的边分别为a,b,c,若bcs C+ccs B=asin A,则△ABC的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若eq \f(sin A,sin B)=eq \f(a,c),(b+c+a)(b+c-a)=3bc,则△ABC的形状为( )
A.直角三角形 B.等腰非等边三角形
C.等边三角形 D.钝角三角形
【答案】 (1)B (2)C
【解析】
(1)法一:因为bcs C+ccs B=asin A,
由正弦定理知sin Bcs C+sin Ccs B=sin Asin A,
得sin(B+C)=sin Asin A.
又sin(B+C)=sin A,得sin A=1,
即A=eq \f(π,2),因此△ABC是直角三角形.
法二:因为bcs C+ccs B=b·eq \f(a2+b2-c2,2ab)+c·eq \f(a2+c2-b2,2ac)=eq \f(2a2,2a)=a,所以asin A=a,即sin A=1,故A=eq \f(π,2),因此△ABC是直角三角形.
(2)因为eq \f(sin A,sin B)=eq \f(a,c),所以eq \f(a,b)=eq \f(a,c),所以b=c.
又(b+c+a)(b+c-a)=3bc,
所以b2+c2-a2=bc,
所以cs A=eq \f(b2+c2-a2,2bc)=eq \f(bc,2bc)=eq \f(1,2).
因为A∈(0,π),所以A=eq \f(π,3),
所以△ABC是等边三角形.
方法总结: 判定三角形形状的途径:①化边为角,通过三角变换找出角之间的关系;②化角为边,通过代数变形找出边之间的关系.正(余)弦定理是转化的桥梁.考查转化与化归思想.
考点三 运用正余弦定理研究三角形的面积
考点03 运用正余弦定理解决三角形的面积
例3、在△ABC中,角A,B,C的对边分别为a,b,c.已知bcsC+ccsB=2acsA.
(1) 求角A的大小;
(2) 若eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))=eq \r(3),求△ABC的面积.
【解析】
:(1) (解法1)在△ABC中,由正弦定理,及bcsC+ccsB=2acsA,
得sinBcsC+sinCcsB=2sinAcsA,
即sinA=2sinAcsA.
因为A∈(0,π),所以sinA≠0,
所以csA=eq \f(1,2),所以A=eq \f(π,3).
(解法2)在△ABC中,由余弦定理,及bcsC+ccsB=2acsA,
得beq \f(a2+b2-c2,2ab)+ceq \f(a2+c2-b2,2ac)=2aeq \f(b2+c2-a2,2bc),
所以a2=b2+c2-bc,所以csA=eq \f(b2+c2-a2,2bc)=eq \f(1,2).
因为A∈(0,π),所以A=eq \f(π,3).
(2) 由eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))=cbcsA=eq \r(3),得bc=2eq \r(3),
所以△ABC的面积为S=eq \f(1,2)bcsinA=eq \f(1,2)×2eq \r(3)×sin60°= SKIPIF 1 < 0
【变式】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a≠b,c=eq \r(3),cs2A-cs2B=eq \r(3)sin Acs A-eq \r(3)sin Bcs B.
(1) 求角C的大小;
(2) 若sin A=eq \f(4,5),求△ABC的面积.
【解析】
:(1) 由题意得 eq \f(1+cs2A,2)-eq \f(1+cs2B,2)=eq \f(\r(3),2)sin 2A-eq \f(\r(3),2)sin 2B,
即eq \f(\r(3),2)sin 2A-eq \f(1,2)cs 2A=eq \f(\r(3),2)sin 2B-eq \f(1,2)cs 2B,sineq \b\lc\(\rc\)(\a\vs4\al\c1(2A-\f(π,6)))=sineq \b\lc\(\rc\)(\a\vs4\al\c1(2B-\f(π,6))).
由a≠b,得A≠B.又A+B∈(0,π),得2A-eq \f(π,6)+2B-eq \f(π,6)=π,即A+B=eq \f(2π,3),所以C=eq \f(π,3).
(2) 由c=eq \r(3),sin A=eq \f(4,5),eq \f(a,sinA)=eq \f(c,sinC),得a=eq \f(8,5).
由a
相关试卷
这是一份新高考数学一轮复习考点精讲练+易错题型第36讲 数列的综合运用(2份打包,原卷版+解析版),文件包含新高考数学一轮复习考点精讲练+易错题型第36讲数列的综合运用原卷版doc、新高考数学一轮复习考点精讲练+易错题型第36讲数列的综合运用解析版doc等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
这是一份新高考数学一轮复习考点精讲练+易错题型第35讲 数列的求和(2份打包,原卷版+解析版),文件包含新高考数学一轮复习考点精讲练+易错题型第35讲数列的求和原卷版doc、新高考数学一轮复习考点精讲练+易错题型第35讲数列的求和解析版doc等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
这是一份新高考数学一轮复习考点精讲练+易错题型第32讲 复数(2份打包,原卷版+解析版),文件包含新高考数学一轮复习考点精讲练+易错题型第32讲复数原卷版doc、新高考数学一轮复习考点精讲练+易错题型第32讲复数解析版doc等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。









