专题05 特殊三角形（知识串讲+13大考点）-2024年中考数学总复习重难考点强化训练（全国通用）

这是一份专题05 特殊三角形（知识串讲+13大考点）-2024年中考数学总复习重难考点强化训练（全国通用），文件包含专题05特殊三角形知识串讲+13大考点全国通用原卷版docx、专题05特殊三角形知识串讲+13大考点全国通用解析版docx等2份试卷配套教学资源，其中试卷共88页， 欢迎下载使用。

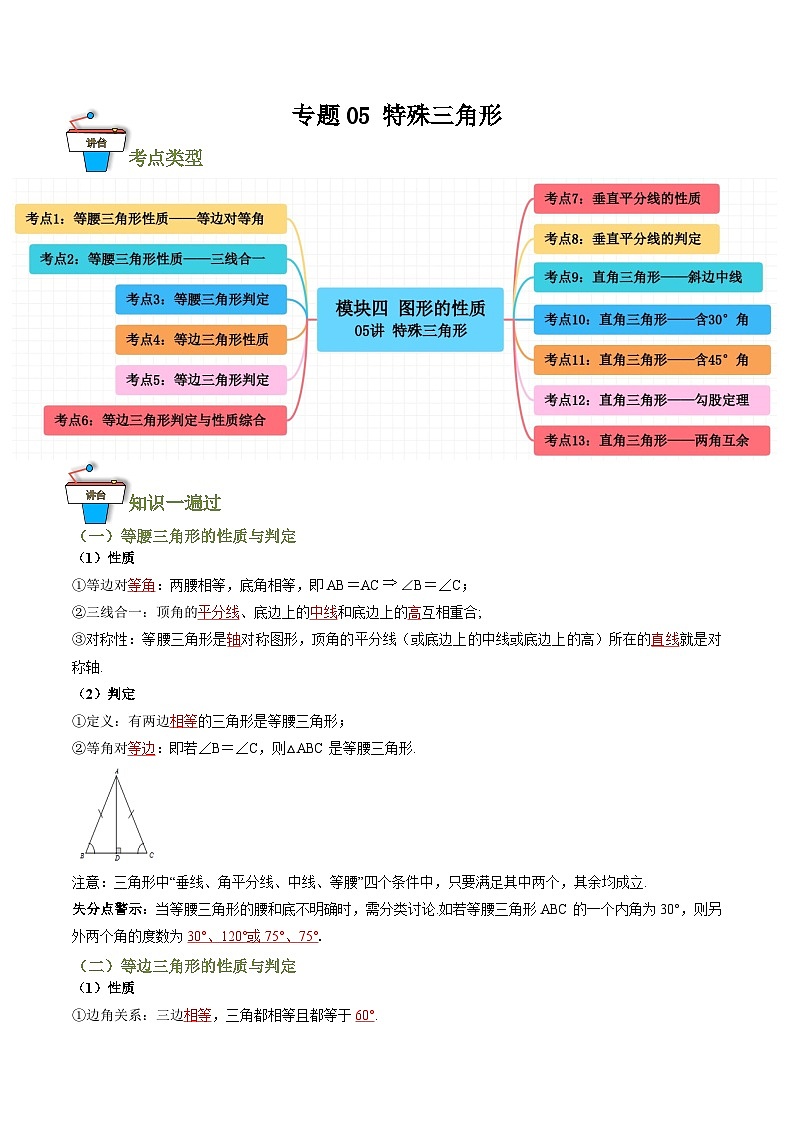
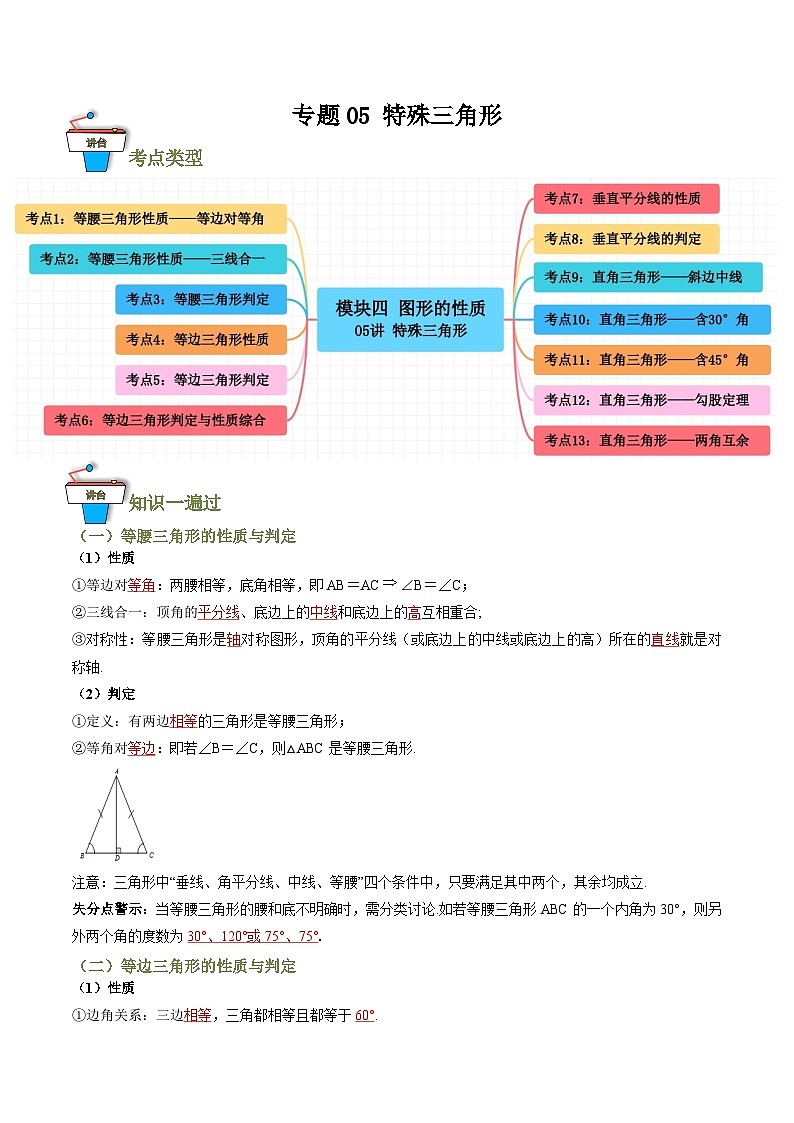
知识一遍过
（一）等腰三角形的性质与判定
（1）性质
①等边对等角：两腰相等，底角相等，即AB＝AC∠B＝∠C；
②三线合一：顶角的平分线、底边上的中线和底边上的高互相重合;
③对称性：等腰三角形是轴对称图形，顶角的平分线（或底边上的中线或底边上的高）所在的直线就是对称轴.
（2）判定
①定义：有两边相等的三角形是等腰三角形；
②等角对等边：即若∠B＝∠C，则△ABC是等腰三角形.
注意：三角形中“垂线、角平分线、中线、等腰”四个条件中，只要满足其中两个，其余均成立.
失分点警示：当等腰三角形的腰和底不明确时，需分类讨论.如若等腰三角形ABC的一个内角为30°，则另外两个角的度数为30°、120°或75°、75°.
（二）等边三角形的性质与判定
（1）性质
①边角关系：三边相等，三角都相等且都等于60°.
②对称性：等边三角形是轴对称图形，三条高线（或角平分线或中线）所在的直线是对称轴.
（2）判定
①定义：三边都相等的三角形是等边三角形；
②三个角都相等（均为60°）的三角形是等边三角形；
③任一内角为60°的等腰三角形是等边三角形.
即若AB＝AC，且∠B＝60°，则△ABC是等边三角形.
注意：（1）等边三角形是特殊的等腰三角形，所以等边三角形也满足“三线合一”的性质.
（2）等边三角形有一个特殊的角60°，所以当等边三角形出现高时，会结合直角三角形30°角的性质，即BD=12AB.
（三）角平分线与垂直平分线的性质
（1）角平分线
①性质：角平分线上的点到角的两边的距离相等．即若
∠1 ＝∠2，PA⊥OA，PB⊥OB，则PA＝PB.
②判定：角的内部到角的两边的距离相等的点在角的角平分线上，即PA=PB。
（2）垂直平分线
①性质：线段的垂直平分线上的点到这条线段的两端点距离相等．即若OP垂直且平分AB，则PA＝PB.
②判定：到一条线段两端点距离相等的点在这条线段的垂直平分线上．

（四）直角三角形的性质
（1）两锐角互余．即∠A＋∠B＝90°；
（2）30°角所对的直角边等于斜边的一半．即若∠B＝30°，则AC＝12AB；
（3）斜边上的中线长等于斜边长的一半．即若CD是中线，则CD＝12AB．
（4）勾股定理：两直角边a、b的平方和等于斜边c的平方．即a2＋b2＝c2．
（五）直角三角形的判定
（1）有一个角是直角的三角形是直角三角形．即若∠C＝90°，则△ABC是直角三角形；
（2）如果三角形一条边的中线等于这条边的一半，那么这个三角形是直角三角形．
即若AD＝BD＝CD，则△ABC是直角三角形
（3）勾股定理的逆定理：若a2＋b2＝c2，则△ABC是直角三角形．
考点一遍过
考点1：等腰三角形的性质——等边对等角
典例1：（2024上·安徽马鞍山·八年级安徽省马鞍山市第七中学校考期末）如图， △ABC≌△ADE，点D在BC上，若∠EAC=30°，则∠ADE的度数为（ ）
A．60°B．65°C．70°D．75°
【变式1】（2013上·江苏苏州·八年级统考期中）如图，△ABC中，以B为圆心，BC长为半径画弧，分别交AC、AB于D、E两点，并连接BD、DE．若∠A=30°，AB=AC，则∠BDE的度数为（ ）
A．67.5°B．52.5°C．45°D．75°
【变式2】（2024上·四川内江·八年级统考期末）如图，△ABC和△ECD都是等腰直角三角形，△ABC的顶点A在△ECD的斜边DE上．下列结论：其中正确的有（ ）
①△ACE≌△BCD ②BD+AD=DE
③∠DAB=∠BCD ④AE2+AD2=2BC2
A．1个B．2个C．3个D．4个
【变式3】（2018·天津河东·八年级统考期末）如图△AOB≌△ADC，∠O=∠D=90°，记∠OAD=α，∠ABO=β，当AO∥BC时，α与β之间的数量关系为（ ）．
A．α+β=90°B．α+2β=180°C．α=βD．α=2β
考点2：等腰三角形的性质——三线合一
典例2：（2024上·河北沧州·八年级统考期末）如图，等腰△ABC的底边BC长为3，面积是6，腰AB的垂直平分线EF分别交AB，AC于点E，F，若点D为底边BC的中点，点M为线段EF上一动点，则△BDM的周长最小值为（ ）
A．4.5B．5C．5.5D．6
【变式1】（2023上·新疆喀什·八年级校联考期中）如图，AC=AB=BD，∠ABD=90°，BC=6，则△BCD的面积为（ ）
A．9B．6C．10 D．12
【变式2】（2023上·山东聊城·八年级校考阶段练习）如图，已知等边△ABC中，点D是AC的中点，点E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M，求证：点M是BE的中点．
【变式3】（2023上·江西南昌·八年级校考阶段练习）如图，在△ABC中，AB=AC，CD垂直AB于D，P为BC上的任意一点，过P点分别作PE⊥AB，PF⊥CA，垂足分别为E，F．
(1)若P为BC边中点，则PE，PF，CD三条线段有何数量关系（写出推理过程）？
(2)若P为线段BC上任意一点，则（1）中关系还成立吗？
【变式4】（2023上·全国·八年级课堂例题）如图①所示，点D，E在△ABC的边BC上，AB=AC．
(1)若AD=AE，求证：BD=CE．
(2)如图②所示，若BD=CE，F为DE的中点，∠BAF=70°，求∠C的度数．
【变式5】（2024上·江苏·八年级姜堰区实验初中校考周测）如图，ΔABC中，AD是边BC上的高，E、F分别是CF、AB的中点，且DC=BF．
(1)判断并说明DE与CF的位置关系；
(2)若AB=10，CF=8，求DE．
考点3：等腰三角形判定
典例3：（2024上·湖南常德·八年级校联考期末）如图所示，在△ABC中，BE平分∠ABC，DE∥BC．
(1)求证：△BDE是等腰三角形；
(2)若∠A=30°，∠C=70°，求∠BDE的度数．
【变式1】（2024上·甘肃武威·八年级校联考期末）如图，在△ABC中，∠ACB=90°，CE是斜边AB上的高，角平分线BD交CE于点M．
(1)求证：△CDM是等腰三角形．
(2)若AB=10,AC=8，求CM的长度．
【变式2】（2024上·湖南长沙·八年级统考期末）如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，过点O作BC的平行线与AB，AC分别相交于点M，N．若AB=5，AC=6，求△AMN的周长．
【变式3】（2023上·江苏苏州·八年级校考阶段练习）如图，将矩形ABCD（AB