




所属成套资源:新高考数学二轮复习课件 专题 (含解析)
新高考数学二轮复习课件 专题九 9.1 直线与圆(含解析)
展开
这是一份新高考数学二轮复习课件 专题九 9.1 直线与圆(含解析),共28页。
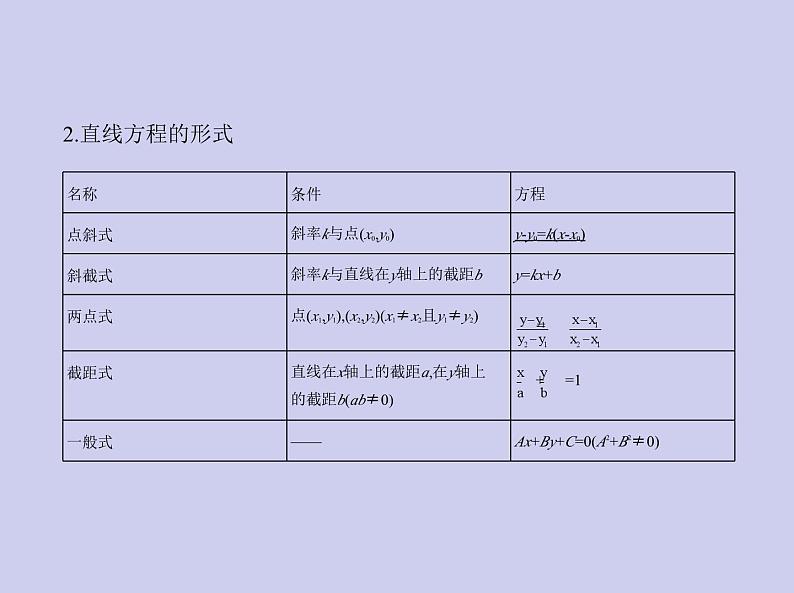
考点一 直线的方程1.直线的倾斜角、斜率1)倾斜角:当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l向上的
方向之间所成的角α叫做直线l的倾斜角.
【注意】 当直线l与x轴平行或重合时,规定l的倾斜角为0°.2)斜率:(角度定义)直线l的倾斜角α≠90°时,斜率k=tan α;(坐标定义)直线l
上两点(x1,y1),(x2,y2)(x1≠x2),则斜率k= .
考点二 圆的方程1.标准方程圆心为(a,b),半径为r的圆的标准方程为(x-a)2+(y-b)2=r2.2.一般方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)表示圆心为 ,半径为 的圆.
1)圆的一般方程的形式特点:①x2和y2的系数相等且大于0;②没有含xy的二次项;③A=C≠0且B=0是二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的必要
不充分条件.2)已知P(x1,y1),Q(x2,y2),则以PQ为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)
=0.
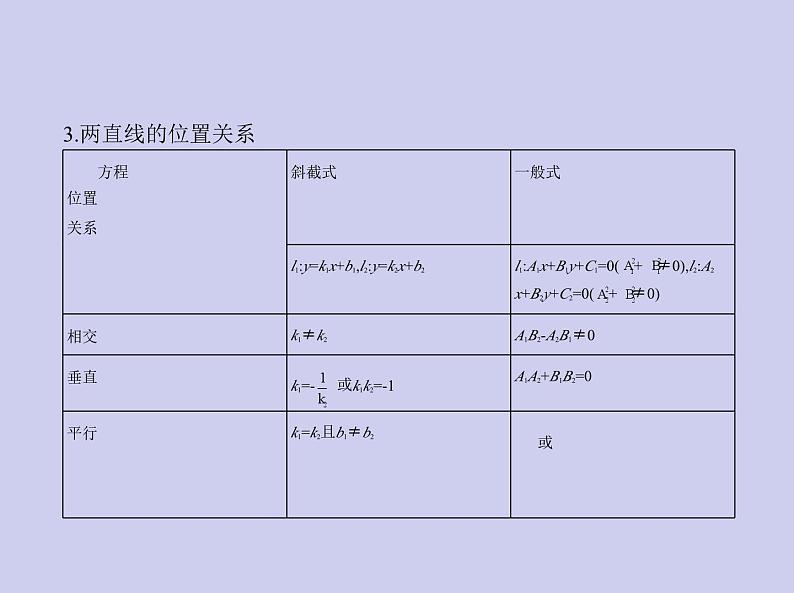
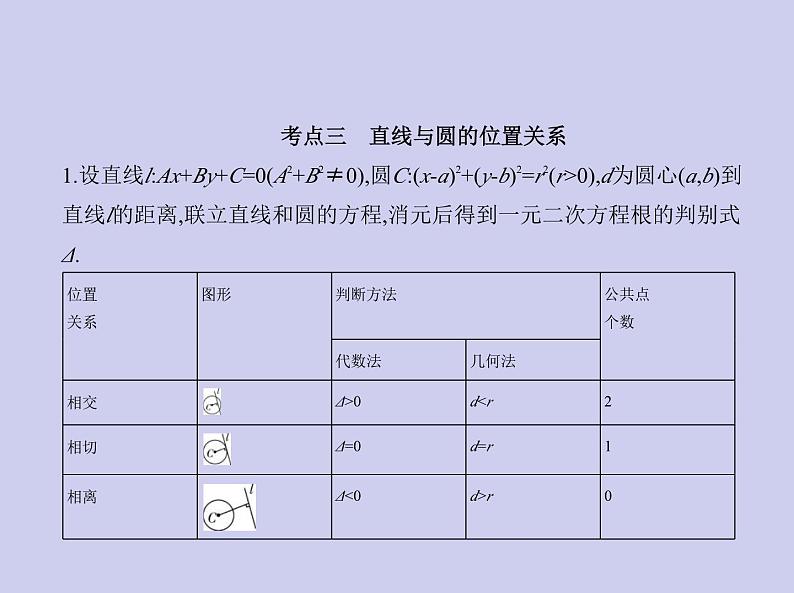
考点三 直线与圆的位置关系1.设直线l:Ax+By+C=0(A2+B2≠0),圆C:(x-a)2+(y-b)2=r2(r>0),d为圆心(a,b)到
直线l的距离,联立直线和圆的方程,消元后得到一元二次方程根的判别式
Δ.
考点四 圆与圆的位置关系1.设两圆的圆心距为d,两圆的半径分别为R,r(R>r),则
【知识拓展】 圆系方程1)同心圆系方程为(x-a)2+(y-b)2=r2(r>0),其中a,b是定值,r是参数;2)过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+
Ey+F+λ(Ax+By+C)=0(λ∈R);3)过圆C1:x2+y2+D1x+E1y+F1=0和圆C2:x2+y2+D2x+E2y+F2=0交点的圆系方程
为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1)(该圆系不含圆C2,解题
时,注意检验圆C2是否满足题意,以防漏解).2.两圆相交时,公共弦所在直线的方程设圆C1:x2+y2+D1x+E1y+F1=0①,圆C2:x2+y2+D2x+E2y+F2=0②,若两圆相交,则
有一条公共弦,由①-②,得(D1-D2)x+(E1-E2)y+F1-F2=0③.方程③表示圆C1与
C2的公共弦所在直线的方程.
考法一 对称问题的处理方法1.中心对称1)若点M(x1,y1)与N(x,y)关于P(a,b)对称,则由中点坐标公式得 2)直线关于点的对称问题可以转化为点关于点的对称问题来解决.2.轴对称1)点关于直线对称求P1(x1,y1)关于直线l:Ax+By+C=0(B≠0)对称的点P2(x2,y2),由线段P1P2的中
点在对称轴l上,而且过点P1,P2的直线垂直于对称轴l,得方程组
可得到点P2的坐标(x2,y2)(其中A≠0,x1≠x2).
2)直线关于直线的对称问题可以转化为点关于直线的对称问题来解决.特别地,①点P(x0,y0)关于直线x=a的对称点为P1(2a-x0,y0).②点P(x0,y0)关于直线y=b的对称点为P2(x0,2b-y0).③点P(x0,y0)关于直线y=x+c的对称点为P3(y0-c,x0+c).④点P(x0,y0)关于直线y=-x+c的对称点为P4(c-y0,c-x0).
例1 已知△ABC的一个顶点A(2,-4),且∠B,∠C的平分线所在直线的方程
分别为x+y-2=0,x-3y-6=0,则BC边所在直线的方程为 .
答案 x+7y-6=0
考法二 圆的切线问题1.求过圆上一点(x0,y0)的切线若切线斜率存在且不为零,则先求切点和圆心连线的斜率k,由垂直关系知
切线斜率为- ,由点斜式可求切线方程;若切线斜率不存在或为零,则可直
接写出切线的方程为x=x0或y=y0.2.求过圆外一点(x0,y0)的切线1)几何法:当切线斜率存在时,设斜率为k,则切线方程为y-y0=k(x-x0),即kx-y
+y0-kx0=0,由圆心到切线的距离等于半径长列出关于k的方程,解方程即可
得到k的值,从而可得切线方程;当切线斜率不存在时,可直接写出切线的
方程为x=x0,检验该直线是不是切线.
2)代数法:当切线斜率存在时,设斜率为k,则切线方程为y-y0=k(x-x0),即y=kx
-kx0+y0,代入圆的方程,得到一个关于x的一元二次方程,由Δ=0求得k值,从
而得到切线方程;当切线斜率不存在时,可直接写出切线的方程为x=x0,检
验该直线是不是切线.
解析 易知圆M的圆心为M(1,2),半径r=3.(1)∵(3-1)2+( +2-2)2=9,∴点P在圆M上,又kPM= = ,∴切线的斜率k=- =- .∴过点P的圆M的切线方程为y-( +2)=- (x-3),即2x+ y-11-2 =0.(2)∵(4-1)2+(3-2)2=9+1=10>9,∴点Q在圆M的外部.①当过点Q的直线的斜率不存在时,直线的方程为x=4,又知点M(1,2)到该
直线的距离d=4-1=3=r,∴直线x=4符合题意.
考法三 圆的弦长问题求圆的弦长通常有两种方法.方法一(几何法):设圆的半径为r,弦心距为d,
弦长为l,则l=2 ;方法二(代数法):设弦所在直线y=kx+b与圆交于A(x
1,y1)、B(x2,y2)两点,联立直线方程与圆的方程,运用根与系数的关系以及弦
长公式得|AB|= · 或|AB|= · (k≠0).
应用一 构建直线、圆模型解决运动实践问题以运动变化为背景考查直线、圆的有关知识,考查数形结合的思想方法,
考查数学建模、直观想象、数学运算的核心素养.这类问题的解决步骤
如下:
相关课件
这是一份新高考数学二轮复习课件 专题九9.2 椭圆及其性质(含解析),共17页。
这是一份新高考数学二轮复习课件专题九9.2 椭圆及其性质(含解析),共17页。
这是一份新高考数学二轮复习课件专题九 9.5 圆锥曲线的综合问题(含解析),共27页。









