新高考数学一轮复习讲义第2章 §2.2　函数的单调性与最值（含解析）

这是一份新高考数学一轮复习讲义第2章 §2.2　函数的单调性与最值（含解析），共15页。

2.掌握函数单调性的简单应用．
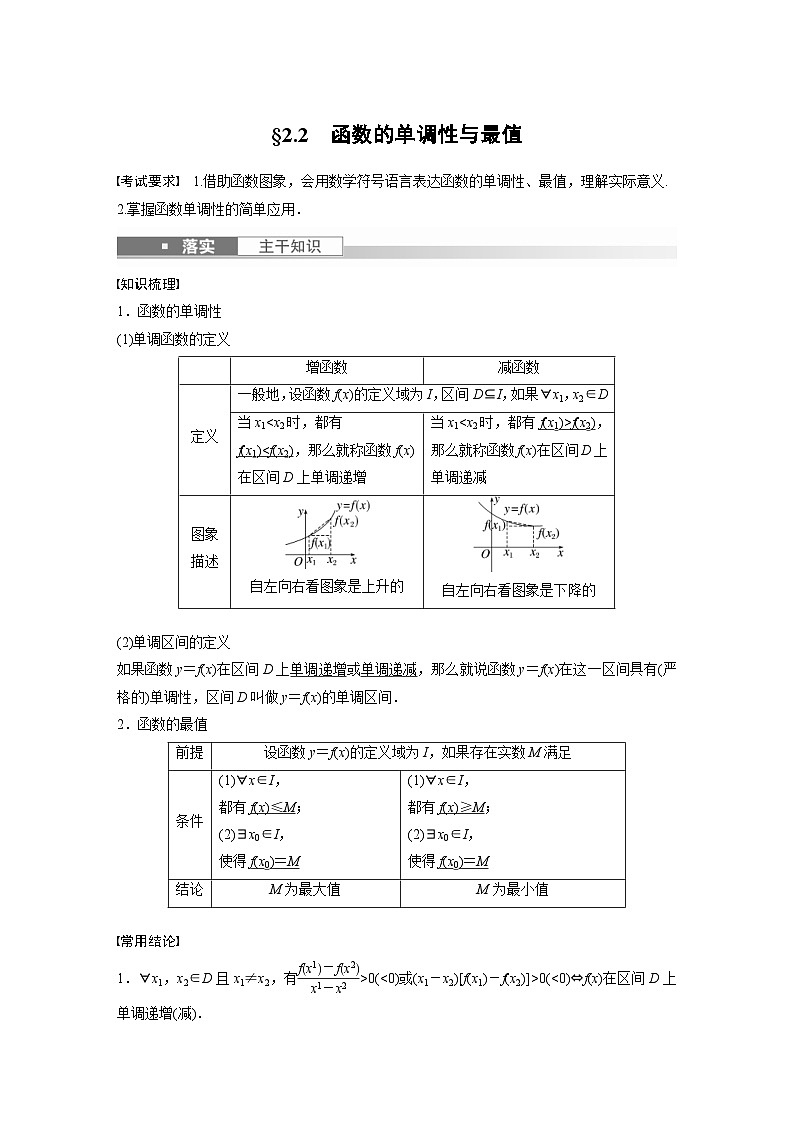
知识梳理
1．函数的单调性
(1)单调函数的定义
(2)单调区间的定义
如果函数y＝f(x)在区间D上单调递增或单调递减，那么就说函数y＝f(x)在这一区间具有(严格的)单调性，区间D叫做y＝f(x)的单调区间．
2．函数的最值
常用结论
1．∀x1，x2∈D且x1≠x2，有eq \f(fx1－fx2,x1－x2)>0(<0)或(x1－x2)[f(x1)－f(x2)]>0(<0)⇔f(x)在区间D上单调递增(减)．
2．在公共定义域内，增函数＋增函数＝增函数，减函数＋减函数＝减函数．
3．函数y＝f(x)(f(x)>0或f(x)<0)在公共定义域内与y＝－f(x)，y＝eq \f(1,fx)的单调性相反．
4．复合函数的单调性：函数y＝f(u)，u＝φ(x)在函数y＝f(φ(x))的定义域上，如果y＝f(u)与u＝φ(x)的单调性相同，那么y＝f(φ(x))单调递增；如果y＝f(u)与u＝φ(x)的单调性相反，那么y＝f(φ(x))单调递减．
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)若f(x)的定义域为R，且f(－3)(2)函数f(x)在(－2,3)上单调递增，则函数的单调递增区间为(－2,3)．( × )
(3)因为y＝x与y＝ex都是增函数，所以y＝xex在定义域内为增函数．( × )
(4)函数y＝eq \f(1,x)的单调递减区间是(－∞，0)∪(0，＋∞)．( × )
教材改编题
1．下列函数中，在区间(0,1)上单调递增的是( )
A．y＝|x＋1| B．y＝2－x
C．y＝eq \f(1,x) D．y＝x2－x＋1
答案 A
2．函数y＝eq \f(x,x－1)在区间[2,3]上的最大值是________．
答案 2
解析 函数y＝eq \f(x,x－1)＝1＋eq \f(1,x－1)在[2,3]上单调递减，当x＝2时，y＝eq \f(x,x－1)取得最大值eq \f(2,2－1)＝2.
3．函数y＝eq \f(a,x－1)在(－∞，1)上为增函数，则实数a的取值范围是________．
答案 (－∞，0)
题型一 确定函数的单调性
命题点1 求具体函数的单调区间
例1 (多选)下列函数在(0，＋∞)上单调递增的是( )
A．y＝ex－e－x B．y＝|x2－2x|
C．y＝x＋cs x D．y＝eq \r(x2＋x－2)
答案 AC
解析 ∵y＝ex与y＝－e－x为R上的增函数，
∴y＝ex－e－x为R上的增函数，故A正确；
由y＝|x2－2x|的图象知，故B不正确；
对于选项C，y′＝1－sin x≥0，
∴y＝x＋cs x在R上为增函数，故C正确；
y＝eq \r(x2＋x－2)的定义域为(－∞，－2]∪[1，＋∞)，故D不正确．
命题点2 判断或证明函数的单调性
例2 试讨论函数f(x)＝eq \f(ax,x－1)(a≠0)在(－1,1)上的单调性．
解 方法一 设－1f(x)＝aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x－1＋1,x－1)))＝aeq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(1,x－1)))，
f(x1)－f(x2)＝aeq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(1,x1－1)))－aeq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(1,x2－1)))
＝eq \f(ax2－x1,x1－1x2－1)，
由于－1所以x2－x1>0，x1－1<0，x2－1<0，
故当a>0时，f(x1)－f(x2)>0，即f(x1)>f(x2)，函数f(x)在(－1,1)上单调递减；
当a<0时，f(x1)－f(x2)<0，
即f(x1)方法二 f′(x)＝eq \f(ax′x－1－axx－1′,x－12)
＝eq \f(ax－1－ax,x－12)＝－eq \f(a,x－12).
当a>0时，f′(x)<0，函数f(x)在(－1,1)上单调递减；
当a<0时，f′(x)>0，函数f(x)在(－1,1)上单调递增．
教师备选
1．设函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(1，x>0，,0，x＝0，,－1，x<0，))g(x)＝x2f(x－1)，则函数g(x)的单调递减区间是__________．
答案 [0,1)
解析 由题意知g(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2，x>1，,0，x＝1，,－x2，x<1，))该函数的图象如图所示，其单调递减区间是[0,1)．
2．已知a>0，函数f(x)＝x＋eq \f(a,x)(x>0)，证明：函数f(x)在(0，eq \r(a)]上单调递减，在[eq \r(a)，＋∞)上单调递增．
证明 方法一 (定义法)设x1>x2>0，
f(x1)－f(x2)＝x1＋eq \f(a,x1)－x2－eq \f(a,x2)
＝(x1－x2)＋eq \f(ax2－x1,x1x2)
＝eq \f(x1－x2x1x2－a,x1x2)，
∵x1>x2>0，∴x1－x2>0，x1x2>0，
当x1，x2∈(0，eq \r(a)]时，0∴x1x2－a<0，
∴f(x1)－f(x2)<0，f(x1)∴f(x)在(0，eq \r(a)]上单调递减，
当x1，x2∈[eq \r(a)，＋∞)时，x1x2>a，
∴x1x2－a>0，∴f(x1)－f(x2)>0，
∴f(x1)>f(x2)，
∴f(x)在[eq \r(a)，＋∞)上单调递增．
方法二 (导数法)
f′(x)＝1－eq \f(a,x2)＝eq \f(x2－a,x2)(x>0)，
令f′(x)>0⇒x2－a>0⇒x>eq \r(a)，
令f′(x)<0⇒x2－a<0⇒0∴f(x)在(0，eq \r(a)]上单调递减，在[eq \r(a)，＋∞)上单调递增．
思维升华 确定函数单调性的四种方法
(1)定义法；(2)导数法；(3)图象法；(4)性质法．
跟踪训练1 (1)函数f(x)＝ln(4＋3x－x2)的单调递减区间是( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(3,2))) B.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3,2)，＋∞))
C.eq \b\lc\(\rc\](\a\vs4\al\c1(－1，\f(3,2))) D.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3,2)，4))
答案 D
解析 f(x)＝ln(4＋3x－x2)的定义域为(－1,4)．
令t＝4＋3x－x2，对称轴为x＝eq \f(3,2)，
故单调递增区间为eq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(3,2)))，
单调递减区间为eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3,2)，4))，
因为y＝ln t为增函数，所以f(x)＝ln(4＋3x－x2)的单调递减区间为eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3,2)，4)).
(2)函数f(x)＝|x－2|x的单调递减区间是________．
答案 [1,2]
解析 f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2－2x，x≥2，,－x2＋2x，x<2.))
画出f(x)的大致图象(如图所示)，
由图知f(x)的单调递减区间是[1,2]．
题型二 函数单调性的应用
命题点1 比较函数值的大小
例3 (2022·成都模拟)已知函数f(x)为R上的偶函数，对任意x1，x2∈(－∞，0)，均有(x1－x2)[f(x1)－f(x2)]<0成立，若a＝f(ln eq \r(2))，b＝f( SKIPIF 1 < 0 )，c＝f( SKIPIF 1 < 0 )，则a，b，c的大小关系是( )
A．cC．a答案 B
解析 ∵对任意x1，x2∈(－∞，0)，
均有(x1－x2)[f(x1)－f(x2)]<0成立，
∴此时函数在区间(－∞，0)上单调递减，
∵f(x)是偶函数，
∴当x∈(0，＋∞)时，f(x)单调递增，
又f(x)＝ SKIPIF 1 < 0 在x∈(0，＋∞)上单调递增，
∴1< SKIPIF 1 < 0 < SKIPIF 1 < 0 ，
又0∴ln eq \r(2)< SKIPIF 1 < 0 < SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 > SKIPIF 1 < 0 >f(ln eq \r(2))，
即a命题点2 求函数的最值
例4 (2022·深圳模拟)函数y＝eq \f(\r(x2＋4),x2＋5)的最大值为________．
答案 eq \f(2,5)
解析 令eq \r(x2＋4)＝t，则t≥2，
∴x2＝t2－4，∴y＝eq \f(t,t2＋1)＝eq \f(1,t＋\f(1,t))，
设h(t)＝t＋eq \f(1,t)，
则h(t)在[2，＋∞)上为增函数，
∴h(t)min＝h(2)＝eq \f(5,2)，
∴y≤eq \f(1,\f(5,2))＝eq \f(2,5)(x＝0时取等号)．
即y的最大值为eq \f(2,5).
命题点3 解不等式
例5 已知函数f(x)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x－lg2(x＋2)，若f(a－2)>3，则a的取值范围是________．
答案 (0,1)
解析 由f(x)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x－lg2(x＋2)知，
f(x)在定义域(－2，＋∞)上是减函数，
且f(－1)＝3，
由f(a－2)>3，得f(a－2)>f(－1)，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(a－2<－1，,a－2>－2，))
解得0命题点4 求参数的取值范围
例6 函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(ax，x≥1，,\b\lc\(\rc\)(\a\vs4\al\c1(4－\f(a,2)))x＋2，x<1，))且满足对任意的实数x1≠x2都有eq \f(fx1－fx2,x1－x2)>0成立，则实数a的取值范围是( )
A．[4,8) B．(4,8)
C．(1,8] D．(1,8)
答案 A
解析 函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(ax，x≥1，,\b\lc\(\rc\)(\a\vs4\al\c1(4－\f(a,2)))x＋2，x<1))满足对任意的实数x1≠x2都有eq \f(fx1－fx2,x1－x2)>0，
所以函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(ax，x≥1，,\b\lc\(\rc\)(\a\vs4\al\c1(4－\f(a,2)))x＋2，x<1))是R上的增函数，
则由指数函数与一次函数的单调性可知应满足eq \b\lc\{\rc\ (\a\vs4\al\c1(a>1，,4－\f(a,2)>0，,a≥4－\f(a,2)＋2，))
解得4≤a<8，
所以实数a的取值范围为[4,8)．
教师备选
1．(2022·嘉峪关模拟)函数f(x)＝ln(x2－ax－3)在(1，＋∞)上单调递增，则a的取值范围是( )
A．(－∞，－2] B．(－∞，－2)
C．(－∞，2] D．(－∞，2)
答案 A
解析 函数f(x)＝ln(x2－ax－3)为复合函数，令u(x)＝x2－ax－3，
y＝ln u为增函数，
故只要u(x)＝x2－ax－3在(1，＋∞)上单调递增即可，只要eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(a,2)≤1，,u1≥0，))
解得a≤－2.
2．对于任意实数a，b，定义min{a，b}＝eq \b\lc\{\rc\ (\a\vs4\al\c1(a，a≤b，,b，a>b.))设函数f(x)＝－x＋3，g(x)＝lg2x，则函数h(x)＝min{f(x)，g(x)}的最大值是______．
答案 1
解析 方法一 在同一坐标系中，作函数f(x)，g(x)的图象，
依题意，h(x)的图象为如图所示的实线部分．
易知点A(2,1)为图象的最高点，
因此h(x)的最大值为h(2)＝1.
方法二 依题意，h(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(lg2x，02.))
当0当x>2时，h(x)＝3－x单调递减，
因此h(x)在x＝2时取得最大值h(2)＝1.
思维升华 (1)比较函数值的大小时，转化到同一个单调区间内，然后利用函数的单调性解决．
(2)求解函数不等式，由条件脱去“f”，转化为自变量间的大小关系，应注意函数的定义域．
(3)利用单调性求参数的取值(范围)．根据其单调性直接构建参数满足的方程(组)(不等式(组))或先得到其图象的升降，再结合图象求解．对于分段函数，要注意衔接点的取值．
跟踪训练2 (1)(2022·天津静海区模拟)已知函数f(x)＝e|x|，记a＝f(lg23)，b＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(lg3\f(1,2)))，c＝f(2.11.2)，则a，b，c的大小关系为( )
A．aC．b答案 C
解析 函数f(x)＝e|x|，其定义域为R，
且f(－x)＝e|－x|＝e|x|＝f(x)，
∴f(x)为偶函数，当x>0时，f(x)＝ex，即函数f(x)在(0，＋∞)上单调递增，
∵2＝lg24>lg23>lg22＝1，
02.11＝2.1>2，
∴2.11.2>lg23>lg32>0，
∴f(2.11.2)>f(lg23)>f(lg32)，
即f(2.11.2)>f(lg23)>f eq \b\lc\(\rc\)(\a\vs4\al\c1(lg3\f(1,2)))，
则b(2)设函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－x2＋4x，x≤4，,lg2x，x>4，))若函数y＝f(x)在区间(a，a＋1)上单调递增，则实数a的取值范围是( )
A．(－∞，1] B．[1,4]
C．[4，＋∞) D．(－∞，1]∪[4，＋∞)
答案 D
解析 画出函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－x2＋4x，x≤4，,lg2x，x>4))的图象，如图，
由图可知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－x2＋4x，x≤4，,lg2x，x>4))的单调递增区间为(－∞，2)，(4，＋∞)，
∵函数在(a，a＋1)上单调递增，
∴a＋1≤2或a≥4，
∴a≤1或a≥4.
(3)已知f(x)是定义在R上的偶函数，且在区间[0，＋∞)上单调递减，则不等式f(2x－1)>f(x＋1)的解集为________．
答案 (0,2)
解析 依题意f(x)是定义在R上的偶函数，且在区间[0，＋∞)上单调递减，所以
f(2x－1)>f(x＋1)⇔(2x－1)2<(x＋1)2，
即4x2－4x＋1即x2－2x＝x(x－2)<0⇒x∈(0,2)．
课时精练
1．下列函数中，在区间(0，＋∞)内单调递减的是( )
A．y＝eq \f(1,x)－x B．y＝x2－x
C．y＝ln x－x D．y＝ex
答案 A
解析 当x∈(0，＋∞)时，y＝eq \f(1,x)与y＝－x单调递减，∴y＝eq \f(1,x)－x在(0，＋∞)上单调递减．
2．若函数f(x)＝eq \f(2x2＋3,1＋x2)，则f(x)的值域为( )
A．(－∞，3] B．(2,3)
C．(2,3] D．[3，＋∞)
答案 C
解析 f(x)＝eq \f(2x2＋3,1＋x2)＝2＋eq \f(1,x2＋1)，
∵x2≥0，∴x2＋1≥1，
∴0∴f(x)∈(2,3]．
3．(2022·贵阳模拟)已知函数f(x)在(－∞，＋∞)上单调递减，且为奇函数，若f(1)＝－2，则满足－2≤f(x－2)≤2的x的取值范围是( )
A．[－2,2] B．[－1,1]
C．[1,3] D．[0,4]
答案 C
解析 因为f(x)为奇函数，
若f(1)＝－2，则f(－1)＝2，
所以不等式－2≤f(x－2)≤2可化为
f(1)≤f(x－2)≤f(－1)，
又f(x)在(－∞，＋∞)上单调递减，
所以－1≤x－2≤1，解得1≤x≤3.
4．(2022·南通模拟)已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(ex－e－x，x>0，,－x2，x≤0，))若a＝50.01，b＝lg32，c＝lg20.9，则有( )
A．f(a)>f(b)>f(c)
B．f(b)>f(a)>f(c)
C．f(a)>f(c)>f(b)
D．f(c)>f(a)>f(b)
答案 A
解析 y＝ex是增函数，y＝e－x是减函数，
因此在(0，＋∞)上y＝ex－e－x单调递增，且此时f(x)>0.
f(x)＝－x2在x≤0时单调递增，
所以f(x)在R上单调递增．
c＝lg20.9<0，b＝lg32，
所以01，
即a>b>c，所以f(a)>f(b)>f(c)．
5．(多选)已知函数f(x)＝x－eq \f(a,x)(a≠0)，下列说法正确的是( )
A．当a>0时，f(x)在定义域上单调递增
B．当a＝－4时，f(x)的单调递增区间为(－∞，－2)，(2，＋∞)
C．当a＝－4时，f(x)的值域为(－∞，－4]∪[4，＋∞)
D．当a>0时，f(x)的值域为R
答案 BCD
解析 当a>0时，f(x)＝x－eq \f(a,x)，
定义域为(－∞，0)∪(0，＋∞)．
∵f(x)在(－∞，0)，(0，＋∞)上单调递增，
故A错误；
又x→－∞时，f(x)→－∞，
x→0－时，f(x)→＋∞，
∴f(x)的值域为R，故D正确；
当a＝－4时，f(x)＝x＋eq \f(4,x)，
由其图象(图略)可知，B，C正确．
6．(多选)已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(ln x＋2x，x>0，,\f(2,1－x)，x≤0，))则下列结论正确的是( )
A．f(x)在R上为增函数
B．f(e)>f(2)
C．若f(x)在(a，a＋1)上单调递增，则a≤－1或a≥0
D．当x∈[－1,1]时，f(x)的值域为[1,2]
答案 BC
解析 易知f(x)在(－∞，0]，(0，＋∞)上单调递增，A错误，B正确；
若f(x)在(a，a＋1)上单调递增，
则a≥0或a＋1≤0，
即a≤－1或a≥0，故C正确；
当x∈[－1,0]时，f(x)∈[1,2]，
当x∈(0,1]时，f(x)∈(－∞，2]，
故x∈[－1,1]时，f(x)∈(－∞，2]，
故D不正确．
7．函数y＝－x2＋2|x|＋1的单调递增区间为__________，单调递减区间为________．
答案 (－∞，－1]和[0,1]
(－1,0)和(1，＋∞)
解析 由于y＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－x2＋2x＋1，x≥0，,－x2－2x＋1，x<0，))
即y＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－x－12＋2，x≥0，,－x＋12＋2，x<0.))
画出函数的图象如图所示，
单调递增区间为(－∞，－1]和[0,1]，单调递减区间为(－1,0)和(1，＋∞)．
8．(2022·山东师大附中质检)已知函数f(x)＝e|x－a|(a为常数)，若f(x)在区间[1，＋∞)上单调递增，则实数a的取值范围是________．
答案 (－∞，1]
解析 f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(ex－a，x≥a，,ea－x，x当x≥a时，f(x)单调递增，当x又f(x)在[1，＋∞)上单调递增，所以a≤1.
9．已知函数f(x)＝ax－eq \f(1,ax)＋eq \f(2,a)(a>0)，且f(x)在(0,1]上的最大值为g(a)，求g(a)的最小值．
解 f(x)＝ax－eq \f(1,ax)＋eq \f(2,a)(a>0)，
∴f(x)在(0,1]上单调递增，
∴f(x)max＝f(1)＝a＋eq \f(1,a)，
∴g(a)＝a＋eq \f(1,a)≥2，当且仅当a＝eq \f(1,a)即a＝1时取等号，
∴g(a)的最小值为2.
10．已知函数f(x)＝a－eq \f(2,2x＋1).
(1)求f(0)；
(2)探究f(x)的单调性，并证明你的结论；
(3)若f(x)为奇函数，求满足f(ax)解 (1)f(0)＝a－eq \f(2,20＋1)＝a－1.
(2)f(x)在R上单调递增．证明如下：
∵f(x)的定义域为R，
∴任取x1，x2∈R且x1则f(x1)－f(x2)＝a－ SKIPIF 1 < 0 －a＋ SKIPIF 1 < 0
＝ SKIPIF 1 < 0 ，
∵y＝2x在R上单调递增且x1∴0< SKIPIF 1 < 0 < SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 － SKIPIF 1 < 0 <0, SKIPIF 1 < 0 ＋1>0, SKIPIF 1 < 0 ＋1>0.
∴f(x1)－f(x2)<0，即f(x1)∴f(x)在R上单调递增．
(3)∵f(x)是奇函数，∴f(－x)＝－f(x)，
即a－eq \f(2,2－x＋1)＝－a＋eq \f(2,2x＋1)，解得a＝1.
∴f(ax)又∵f(x)在R上单调递增，∴x<2.
∴x的取值范围是(－∞，2)．
11．定义max{a，b，c}为a，b，c中的最大值，设M＝max{2x,2x－3,6－x}，则M的最小值是( )
A．2 B．3 C．4 D．6
答案 C
解析 画出函数M＝max{2x,2x－3,6－x}的图象(如图)，由图可知，
函数M在A(2,4)处取得最小值22＝6－2＝4，
故M的最小值为4.
12．如果几个函数的定义域相同、值域也相同，但解析式不同，称这几个函数为“同域函数”. 函数y＝eq \r(x－1)－eq \r(2－x)的值域为________，则与y是“同域函数”的一个解析式为________．
答案 [－1,1] y＝2x－3，x∈[1,2] 或y＝sin(2πx)，x∈[1,2]或y＝3x－1－2，x∈[1,2](答案不唯一)
解析 因为y＝eq \r(x－1)－eq \r(2－x)，
所以x≥1且x≤2，
所以函数的定义域为[1,2]．
显然，函数y＝f(x)＝eq \r(x－1)－eq \r(2－x)在[1,2]上单调递增，
所以f(x)∈[－1,1]，
所以函数的值域为[－1,1]．
只要满足定义域为[1,2]，且值域为[－1,1]的函数均符合题意，
例如y＝sin(2πx)，x∈[1,2]或y＝2x－3，x∈[1,2]或y＝3x－1－2，x∈[1,2]．
13．设函数f(x)＝eq \f(ax＋1,x＋2a)在区间(－2，＋∞)上单调递增，那么a的取值范围是________．
答案 [1，＋∞)
解析 f(x)＝eq \f(ax＋2a2－2a2＋1,x＋2a)＝a－eq \f(2a2－1,x＋2a)，
定义域为{x|x≠－2a}，
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(2a2－1>0，,－2a≤－2，))
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(2a2－1>0，,a≥1，))所以a≥1.
14．(2022·沧州模拟)设函数f(x)＝x3－sin x＋x，则满足f(x)＋f(1－2x)<0的x的取值范围是________．
答案 (1，＋∞)
解析 f(x)＝x3－sin x＋x，
∵f(－x)＝(－x)3－sin(－x)＋(－x)
＝－(x3－sin x＋x)＝－f(x)，
∴f(x)为奇函数，
又f′(x)＝3x2－cs x＋1≥0，
∴f(x)为R上的增函数，
∴f(x)＋f(1－2x)<0可化为
f(x)<－f(1－2x)＝f(2x－1)，
∴x<2x－1，即x>1，
∴满足f(x)＋f(1－2x)<0的x的取值范围是(1，＋∞)．
15．(2022·厦门模拟)函数g(x)＝ax＋2(a>0)，f(x)＝x2－2x，对∀x1∈[－1,2]，∃x0∈[－1,2]，使g(x1)＝f(x0)成立，则a的取值范围是( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,3))) B．[1,2)
C.eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,2))) D.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(1,3)，＋∞))
答案 C
解析 若对∀x1∈[－1,2]，∃x0∈[－1,2]，
使g(x1)＝f(x0)成立，
只需函数y＝g(x)的值域为函数y＝f(x)的值域的子集即可．
函数f(x)＝x2－2x＝(x－1)2－1，x∈[－1,2]的值域为[－1,3]．
当a>0时，g(x)＝ax＋2单调递增，
可得其值域为[2－a,2＋2a]，
要使[2－a,2＋2a]⊆[－1,3]，
需eq \b\lc\{\rc\ (\a\vs4\al\c1(2－a≥－1，,2＋2a≤3，,a>0，))
解得0综上，a的取值范围为eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,2))).
16．已知定义在R上的函数f(x)满足f(x＋y)＝f(x)＋f(y)＋1，且当x>0时，f(x)>－1.
(1)求f(0)的值，并证明f(x)在R上是增函数；
(2)若f(1)＝1，解关于x的不等式f(x2＋2x)＋f(1－x)>4.
解 (1)令x＝y＝0，得f(0)＝－1.
在R上任取x1>x2，则x1－x2>0，
所以f(x1－x2)>－1.
又f(x1)＝f[(x1－x2)＋x2]＝f(x1－x2)＋f(x2)＋1>f(x2)，
所以函数f(x)在R上是增函数．
(2)由f(1)＝1，得f(2)＝3，f(3)＝5.
由f(x2＋2x)＋f(1－x)>4得f(x2＋x＋1)>f(3)，
因为函数f(x)在R上是增函数，
所以x2＋x＋1>3，
解得x<－2或x>1，
故原不等式的解集为{x|x<－2或x>1}．增函数
减函数
定义
一般地，设函数f(x)的定义域为I，区间D⊆I，如果∀x1，x2∈D
当x1f(x1)当x1f(x2)，那么就称函数f(x)在区间D上单调递减
图象描述
自左向右看图象是上升的
自左向右看图象是下降的
前提
设函数y＝f(x)的定义域为I，如果存在实数M满足
条件
(1)∀x∈I，
都有f(x)≤M；
(2)∃x0∈I，
使得f(x0)＝M
(1)∀x∈I，
都有f(x)≥M；
(2)∃x0∈I，
使得f(x0)＝M
结论
M为最大值
M为最小值