海南省东方市2024届九年级下学期中考二模数学试卷(含答案)

这是一份海南省东方市2024届九年级下学期中考二模数学试卷(含答案)，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

数学试卷
温馨提示：本卷满分120分，考试时间100分钟，请将答案写在答题卡上
一、选择题（本大题36分，每小题3分，在下列各题的四个备选答案中，有且只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑）
1. 实数的相反数是（ ）
A. 5B. C. D.
2. 如图是一个由5个相同的正方体组成的立体图形，它的主视图是（ ）
A. B. C. D.
3. 根据《海南省2024年第一季度直排海污染浓度上报表》数据显示，东方市污水处理厂污水排放口第一季度污水排放量约2679800吨，数据2679800用科学记数法表示（ ）
A. B. C. D.
4. 下列计算正确的是（ ）
A. B. C. D.
5. 九年级(1)班7名同学在某次“1分钟仰卧起坐”的测试中，成绩如下（单位：次）：38，39，39，40，41，42，45，这组数据的众数、中位数分别是（ ）
A. 39，40B. 39，38C. 40，38D. 40，39
6. 分式方程的解是（ ）
A. B. C. D.
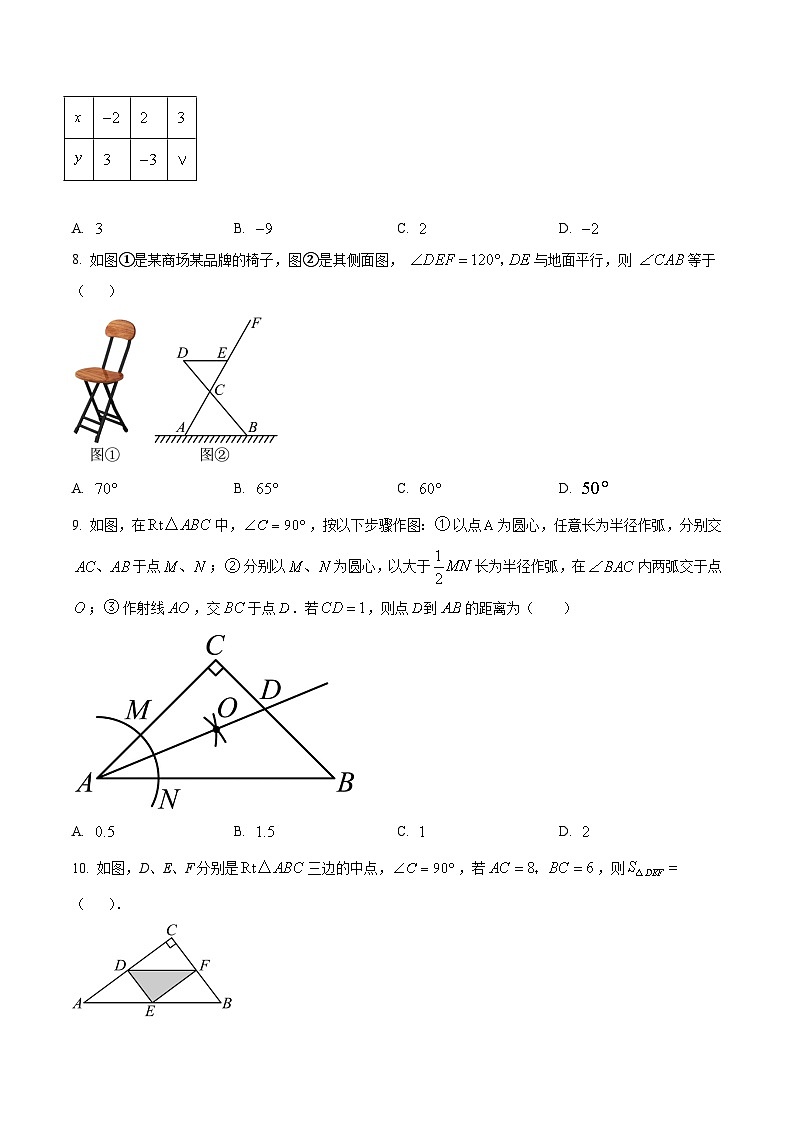
7. 已知是的反比例函数，如表给出了与的一些值，表中处的数为（ ）
A. B. C. D.
8. 如图①是某商场某品牌的椅子，图②是其侧面图， 与地面平行，则 等于（ ）
A. B. C. D.
9. 如图，在中，，按以下步骤作图：以点为圆心，任意长为半径作弧，分别交于点；分别以为圆心，以大于长为半径作弧，在内两弧交于点；作射线，交于点．若，则点到的距离为（ ）
A. B. C. D.
10. 如图，D、E、F分别是三边的中点，，若，则（ ）．
A. 7B. 6C. 5D. 4
11. 如图，是的直径，，则（ ）

A. B. C. D.
12. 如图是于我国汉代数学家赵爽的弦图，它是由四个全等直角三角形与一个小正方形拼成的一个大正方形．若小正方形的面积为，大正方形的面积为，直角三角形中较小的锐角为，则的值为（ ）
A. B. C. D.
二、填空题（本大题满分12分，每小题3分）
13. 因式分解：ax﹣ay=_____．
14. 某蓄电池电压为，使用此蓄电池时，电流I（单位：A）与电阻R（单位：Ω）的函数表达式为，当时，I的值为____A．
15. 如图，在平行四边形中，，将线段水平向右平移个单位长度得到线段EF，若四边形为菱形时，则a的值为_____．
16. 如图，在平面直角坐标系中，的顶点B在x轴的正半轴上，点A的坐标为，将绕点O逆时针旋转，使点B的对应点落在边上，连接A、，则____，线段的长度是_____．
三、解答题（本大题满分72分）
17. 计算：
（1）计算：；
（2）解不等式组：.
18. 为创建文明校园，某中学计划在学校公共场所安装垃圾箱和温馨提示牌，已知，安装3个垃圾箱和2个温馨提示牌需340元，安装1个垃圾箱比1个温馨提示牌多30元．求安装1个垃圾箱和1个温馨提示牌各需多少元？
19. 年龙年“春节”期间，海南景区人头攒动，热闹非凡．东方市旅游和文化广电体育局随机抽取若干名选择来我市的游客进行了问卷调查．调查问卷（节选）如下：
调查问卷
根据统计得到的数据，绘制成下面两幅不完整的统计图：
请根据统计图中提供信息，解答下面的问题：
（1）本次参加抽样调查的游客有 人，喜欢海南花梨谷文化旅游区的游客有 人；
（2）在扇形统计图中，喜欢俄贤岭生态文化旅游区的游客人数所占圆心角为 度；
（3）从参加抽样调查的游客中任选一名，恰好最喜欢的旅游景点是鱼鳞洲的概率是 ；
（4）据不完全统计，龙年春节期间，省内外游客约万人次畅游东方，请估算来鱼鳞洲风景区的游客约 万人次．
20. 如图，在东西方向的海岸线l上有一长为的码头，在码头西端M的正西方向有一观察站A，，某时刻测得A处的北偏西且与A相距的B处，有一艘匀速直线航行的轮船，轮船沿南偏东45°的方向航行，经过2小时，又测得该轮船位于A处的北偏东方向的C处．（参考数据：）
（1）填空： = ； ；
（2）求轮船航行的速度（结果保留根号）；
（3）如果该轮船不改变航向继续航行，那么轮船能否正好航行至码头靠岸？请说明理由．
21. 已知，在正方形中，，点分别在边上，连接．
（1）如图，若于点，求证：；
（2）在（）的条件下，若为的中点，
为中点，求出的长；
如图，连接，求证：；
（3）如图，若，求出最小值．
22. 如图1，抛物线过点．
（1）求抛物线的解析式；
（2）设点P是第一象限内抛物线上的一个动点，
①当P为抛物线的顶点时，求证：是直角三角形；
②求出的最大面积及此时P点的坐标；
③如图2，过点P作轴，垂足为N，与交于点E．当的值最大时，求点P的坐标．
参考答案
一、选择题
1. A
2. B
3. C
4. D
5. A
6. D
7. D
8. C
9. C
10. B
11. B
12. A
二、填空题
13. a（x-y）.
14. 5
15. 2
16. ①. 1 ②. 2
三、解答题
17. （1）解：
．
（2）解：，
解不等式①可得：，
解不等式②可得：．
所以该不等式的解集为．
18. 解：设安装1个垃圾箱需要x元，1个温馨提示牌需要y元，
根据题意得：，解得：．
答：安装1个垃圾箱和1个温馨提示牌分别是80、50元．
19. （1）解：本次参加抽样调查的游客人数为人，
∴喜欢海南花梨谷文化旅游区的游客人数为人，
故答案为：，；
（2）解：喜欢俄贤岭生态文化旅游区的游客人数所占圆心角为，
故答案为：；
（3）解：从参加抽样调查游客中任选一名，恰好最喜欢的旅游景点是鱼鳞洲的概率是，
故答案为：；
（4）解：，
∴估算来鱼鳞洲风景区的游客约万人次，
故答案为：．
20. （1）解：由题意可得：
,，
∴，
∴；
∵，
∴,
∵，
∴．
故答案为：．
（2）解：∵，，
∴，
∴为直角三角形．
∵，
∴，
∴，
∴轮船航行的速度（千米/小时）．
（3）解：能．理由如下：
如图：延长航线角直线l与点T．
∵，，
∴,
∵,
∴,
∵,
∴，
∴轮船能够正好行至码头靠岸．
21. (1)证明：∵四边形是正方形，
∴，，
∴，
∵，
∴，
∴，
即，
∴，
(2)解：∵为的中点，
∴，
∵，
∴，
∴，
∴，
∵，
∴，
∵为的中点，
∴；
如图，过点作于，则，
∴，
∵，
∴，
∵为的中点，
∴，
∴，
∴，
设，，则，，
在中，，
∴，
解得，
∴，
在中，，
∴，
∴，
∴，，
∴，
∴，
∴；
(3)解：连接，
∵，
∴，
∴，
∴，
作点关于的对称点，连接，则，
∴，
∵
∴当点三点共线时，的值最小，即为的长度，
∴最小值．
22. （1）解：把两点坐标代入可得：
，解得：，
∴抛物线的解析式为．
（2）解：①配方得，
∴点P的坐标为，
当时，，即，
作轴于点H，则，
∴，
∵，，
∴，
又∵，
∴，
∴，
∴是直角三角形．
②设直线的解析式为，将点B、C代入得：
，解得：，
∴直线的解析式为，
设点，
如图：过点P作轴于点D，交于点E，
∴，
∴，
∴，
当时，的最大面积为，，
∴．
③设点，
如图：过点P作轴于点N，交于点E，
∴，
∴，
∵，，
∴，，
∴，
∴，
∴，
∴，
∴，
∴当时，有最大值，此时．