3.2.2 利用公式列关系式并求值 （课件）--2024-2025学年人教版数学七年级上册

这是一份3.2.2 利用公式列关系式并求值 （课件）--2024-2025学年人教版数学七年级上册，共26页。

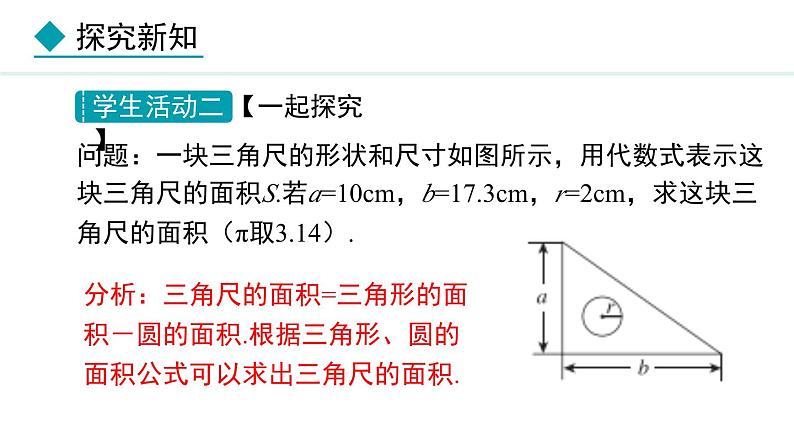
第三章 代数式 3.2 代数式的值 第2课时 利用公式列关系式并求值 1.通过经历列代数式解决问题的过程，进一步理解列代数式和求代数式的值的的实际意义，感受其中的抽象思维和符号意识；2.通过结合已有知识的认知和实际问题求解的经历，体会实际问题中同类事物中的数量关系可以以公式的形式进行描述，感受用数字、字母、符号等表示的代数式的简洁性、一般性，进一步培养学生的应用意识；3.通过分析和利用实际问题中的数量关系解决问题的过程，发展学生的阅读理解、总结归纳的能力，进一步提高学生分析问题、解决问题的能力。学习重点：会利用实际问题中的数量关系求出代数式的值．学习难点：能够准确地把握实际问题中同类事物中固有的数量关系，并利用其解决实际问题.问题：李明同学到文具商店为学校美术组的20名同学购买铅笔和橡皮，已知铅笔每支m元，橡皮每块n元，若给每名同学买3支铅笔和2块橡皮，（1）用代数式表示李明同学一共需付款______元；（2）若m=3元，n=1.5元时，求这次李明购买铅笔和橡皮共需付款多少元？分析：本题中涉及到三个量：总价、单价和数量，它们之间的数量关系是：总价=单价×数量.解：（1）20（3m+2n）.（2）当m=3，n=1.5时，20（3m+2n）=20×（3×3+2×1.5）=240.问题：如图，某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成，其中直道的长为a，半圆形弯道的直径为b.（1）用代数式表示这条跑道的周长；（2）当a=67.3m，b=52.6m时，求这条跑道的周长（π取3.14，结果取整数）.分析：跑道的周长是两段直道和两段弯道的长度和.由圆的周长公式可以求出弯道的长度.解：(1)两段直道的长为2a；两段弯道组成一个圆，它的直径为b，周长为πb，因此，这条跑道的周长为2a+πb.(2)当a=67.3 m，b=52.6m时，2a+πb=2×67.3+3.14×52.6≈300(m).因此，这条跑道的周长约为300 m.本题中用到了圆的周长公式2πr或πd，圆的面积公式你知道吗？其他图形的呢？问题：一块三角尺的形状和尺寸如图所示，用代数式表示这块三角尺的面积S.若a=10cm，b=17.3cm，r=2cm，求这块三角尺的面积（π取3.14）.分析：三角尺的面积=三角形的面积－圆的面积.根据三角形、圆的面积公式可以求出三角尺的面积. 1.一些相近的或同类的事物中所蕴含的数量关系往往是一致的，因此可以用一些通用的公式来描述，比如销售问题中的数量关系：总价=单价×数量、圆面积=πr2、工作总量=工作效率×工作时间等等，都是这些问题情境中所固有的数量关系；2.在解决实际问题的时候，要善于分析实际问题中量与量之间的关系，抓住这些问题中的数量关系，列代数式进行求解；3.用代数式可以更简洁、更一般地表示实际问题中的数量关系；4.列代数式并求代数式的值可以解决很多实际问题.问题：甲、乙两地间的公路全长100千米，某人从甲地到乙地每小时走m千米，用代数式表示：(1)此人从甲地到乙地需要走______小时；(2)如果每小时多走5千米，此人从甲地到乙地需要走______小时；则此人从甲地到乙地少用______小时．（3）若m=20千米，则此人加速后，从甲地到乙地少用几小时？     1.某企业生产一批电视机，每天生产m台，计划生产a天．为适应市场需求，需要提前3天完成，用代数式表示出实际每天要多生产多少台电视机？并求出当m＝100，a＝28时，每天多生产的电视机的台数．  2.我国是一个严重缺水的国家，大家都应该加倍珍惜水资源，节约用水．据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约0.05毫升．小康同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小康离开x分钟后，水龙头滴出y毫升的水．（1）用含x的代数式表示y．（2）当小康离开10分钟后，水龙头滴水多少毫升？解：（1）y＝5x．（2）50毫升．3.某种铂金饰品在甲、乙两个商店销售．甲店标价477元/克，按标价出售，不优惠．乙店标价530元/克，但若买的铂金饰品重量超过3克，则超出部分可打八折出售．（1）分别写出到甲、乙商店购买该种铂金饰品所需费用y（元）和重量x（克）（x大于3）之间的关系式；（2）李阿姨要买一条重量为5克的此种铂金饰品，到哪个商店购买更合算？（1）分别写出到甲、乙商店购买该种铂金饰品所需费用y（元）和重量x（克）（x大于3）之间的关系式；（2）李阿姨要买一条重量为5克的此种铂金饰品，到哪个商店购买更合算？解：（1）y甲＝477x，y乙＝530×3＋530（x－3）·80%．（2）当x＝5时，y甲＝2385，y乙＝2438．所以买5克时，到甲商店购买更合算．1.时代中学八年级有x名同学参加植树，平均每人植树3棵；七年级有y名同学参加参加植树，平均每人植树2棵。①该校七、八年级同学共植树多少棵？②如果x=98,y=102,那么这个学校七、八年共植树木多少棵？解：①八年级同学共植树____棵七年级同学共植树____棵， 该校七年级八年级共植树_______ 棵。②当x=98，y=102时，3x+2y=3×98+2×102=498(棵） 3x2y3x+2y2.天泉村去年的小麦产量为a吨，今年比去年增加了10%，今年的小麦总产量是多少吨？如果去年的小麦总产量是480吨，今年的小麦总产量是多少吨？解：今年小麦总产量：a（1+10％）=1.1a,当a=480时，1.1a=1.1×480=528（吨）.答：今年的小麦总产量是528吨.3.请根据图示的对话解答下列问题．（1）求：a，b，c的值．（2）计算7－a＋3b－c值．解：（1）∵a的相反数是－3，b的绝对值是6，∴a＝3，b＝±6．∵a＞b，∴b＝－6．∵b与c的和是－9，∴c＝－9－（－6）＝－9＋6＝－3．（2）当a＝3，b＝－6，c＝－3时， 7－a＋3b－c ＝7－3＋3×（－6）－（－3） ＝7－3＋（－18）＋3 ＝－11． 完成课后练习题.