人教版（2024）九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数教案

这是一份人教版（2024）九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数教案，共3页。教案主要包含了师生互动，点导评析，监测反馈等内容，欢迎下载使用。
22.3 二次函数与特殊四边形问题
上课教师
上课时间
教学
目标
1. 能建立二次函数图像解决与几何图形相关的实际问题。
2. 会用函数图像的性质和图像解决问题。
3. 能综合运用分类方法解决与二次函数图像相关的特殊四边形。
教学
重点
能建立二次函数图像解决与几何图形相关的问题。
教学
难点
能综合运用分类方法解决与二次函数图像相关的特殊四边形。
教 学 过 程
环节
教师活动
学生活动
设计意图
课前预习
布置学生的课前预习任务；
进行预习方法指导；
3、对学生预习任务进行检查与评定。
1、认真阅读教材51页内容，用铅笔勾画重点概念；
2、完成《练习册》44-45页例1、例2。
培养学生课前预习习惯，提升学生自主学习能力。
自主学习
理解新知
一、师生互动、引问激思（运用教材，梳理知识）
1、平行四边形的问题
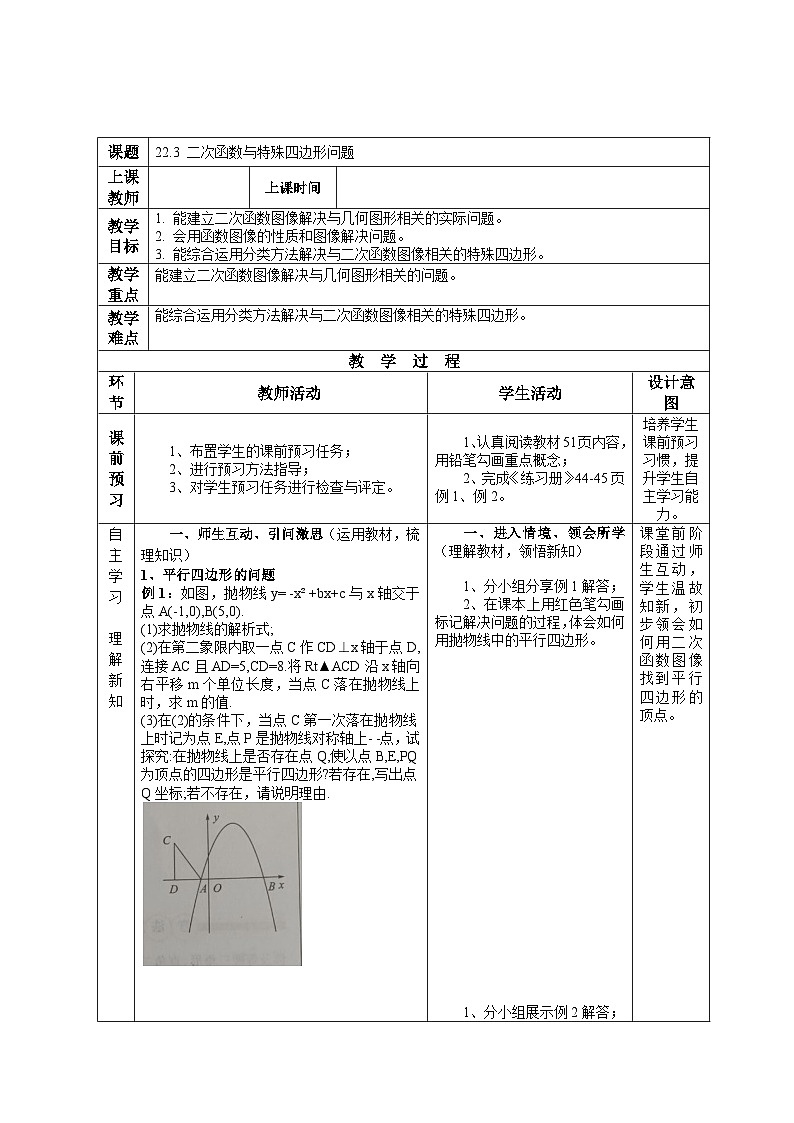
例1：如图，抛物线y= -x² +bx+c与x轴交于点A(-1,0),B(5,0).
(1)求抛物线的解析式;
(2)在第二象限内取一点C作 CD⊥x轴于点D,连接AC且AD=5,CD=8.将Rt▲ACD沿x轴向右平移m个单位长度，当点C落在抛物线上时，求m的值.
(3)在(2)的条件下，当点C第一次落在抛物线 上时记为点E,点P是抛物线对称轴上- -点，试探究:在抛物线上是否存在点Q,使以点B,E,P,Q为顶点的四边形是平行四边形?若存在,写出点Q坐标;若不存在，请说明理由.
例2：如图,抛物线与y轴交于点A，过点A的直线与抛物线交于另一点B，过点B做BC⊥X轴于点C（3，0）.
求直线AB的函数解析式；
动点P在OC上从原点O出发以每秒一个单位长度的速度向点C移动，过点P作PN⊥x轴交直线AB于M,交抛物线于N.设点P运动时间为t秒,MN长为s个单位长度,求s与t的两数关系式并求t的取值范围:
(3)在(2)的条件下(不考虑点P与点0,C重合 情况) ,连接CM,BN,当t为何值时四边形BCMN为平行四边形?对于所求的t值，平行四边形BCMN可否为菱形?说明理由.
一、进入情境、领会所学（理解教材，领悟新知）
1、分小组分享例1解答；
2、在课本上用红色笔勾画标记解决问题的过程，体会如何用抛物线中的平行四边形。
1、分小组展示例2解答；
2、说出菱形的特点
3、勾画课本上相应的重点语句；
4、范书写例题解答格式。

课堂前阶段通过师生互动，学生温故知新，初步领会如何用二次函数图像找到平行四边形的顶点。
类比例1，修订不规范解答，为后续变式练习作铺垫。
通过例1、2理解如何建立二次函数图像找到特殊四边形的顶点。
互动交流
巩固所学
二、点导评析、归类拓展（运用教辅，解疑释惑）
例1变式：如图，在平面直角坐标系中的，直线y=0.5x²+2与x轴交于点A，与y轴交于点B，抛物线y=-0.5x²+bx+c经过点A、B，且与x轴的负半轴交于点C.
求该抛物线的解析式；
已知E、F分别是直线AB和抛物线上的动点，当以B,O,E,F,为顶点的四边形是以OB为一条边的平行四边形时，求出所有符合条件的点E的坐标。
例2变式：已知点A( -1,0),B(3,0),是否存在过A,B两点的抛物线，其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出抛物线的解析式。
课堂小结：《练习册》第45页“方法归纳”。
二、课堂展示、体系建构(例题展示，变式操练)
1、会规范快速求解
2、准确说清解题依据；
1、进一步应用二次函数解决特殊四边形；
2、开动脑筋，快速求解
1、将课堂小结的两个知识点在课本上做好简要笔记。
课堂中阶段通过变式训练，进一步巩固所学，拓展知识，为当堂测评高过关率作好充分的铺垫。进一步规范解题格式，探索解题思想方法，归纳所学，建构认知体系。
当堂测评
分享收获
三、监测反馈、辅导调整（精选试题，实施检测）
1、当堂测评：《白册子》第59页：1、2、3、4、5（每题20分，共100分），附加题：12（50分）
2、课堂巡视，了解检测情况，个别面辅，收集共性问题在练习课上重点解决。
3、选择性点评共性问题。
兴趣信心、互助提升（满意高分，组间争雄）
1、独立作答，仔细检查，余下的考试时间完成当天课后作业题。
2、组间交换批阅或收交教师批阅，试题返还后，组长统分，统计好小组评比加分表，交科代表汇总上报老师。
3、先独立安静纠错，无法解决的问题可轻声请教组内同学“一帮一”。
课堂后阶段通过当堂测评反馈教学效果，及时解决存在问题。多数学生能考出高分数，分享学习数学的愉悦。
课后作业
课后作业：《白册子》59-60页6、7、8、9、10、11题。余下各题学有余力学生选做（难题教师要课后个别指导）。
教学反思