新高考数学一轮复习学案 第4章 §4.5 函数y＝Asin(ωx＋φ)的图象及应用（含解析）

这是一份新高考数学一轮复习学案 第4章 §4.5 函数y＝Asin(ωx＋φ)的图象及应用（含解析），共19页。

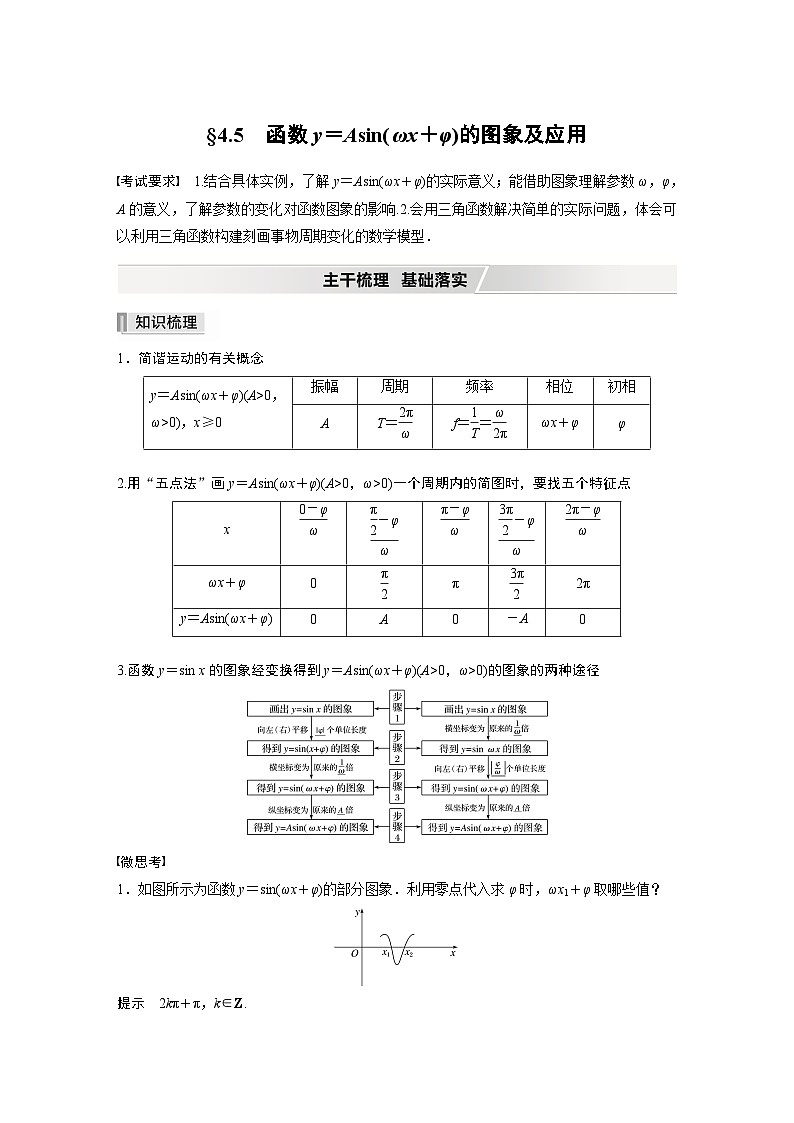
1．简谐运动的有关概念
2.用“五点法”画y＝Asin(ωx＋φ)(A>0，ω>0)一个周期内的简图时，要找五个特征点
3.函数y＝sin x的图象经变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种途径
微思考
1．如图所示为函数y＝sin(ωx＋φ)的部分图象．利用零点代入求φ时，ωx1＋φ取哪些值？
提示 2kπ＋π，k∈Z.
2．函数y＝sin(ωx＋φ)图象的对称轴是什么？对称中心是什么？
提示 对称轴是直线x＝eq \f(kπ,ω)＋eq \f(π,2ω)－eq \f(φ,ω)(k∈Z)，
对称中心是点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,ω)－\f(φ,ω)，0))(k∈Z)．
题组一 思考辨析
1．判断下列结论是否正确(请在括号中打“√”或“×”)
(1)把y＝sin x的图象上各点的横坐标缩短为原来的eq \f(1,2)，纵坐标不变，所得图象对应的函数解析式为y＝sin eq \f(1,2)x.( × )
(2)将y＝sin 2x的图象向右平移eq \f(π,6)个单位长度，得到y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))的图象．( √ )
(3)函数f(x)＝Asin(ωx＋φ)(A≠0)的最大值为A，最小值为－A.( × )
(4)如果y＝Acs(ωx＋φ)的最小正周期为T，那么函数图象的相邻两个对称中心之间的距离为eq \f(T,2).( √ )
题组二 教材改编
2．函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x－\f(π,3)))的振幅、频率和初相分别为( )
A．2,4π，eq \f(π,3) B．2，eq \f(1,4π)，eq \f(π,3)
C．2，eq \f(1,4π)，－eq \f(π,3) D．2,4π，－eq \f(π,3)
答案 C
解析 由题意知A＝2，f＝eq \f(1,T)＝eq \f(ω,2π)＝eq \f(1,4π)，初相为－eq \f(π,3).
3．函数y＝sin x的图象上所有点的纵坐标不变，横坐标伸长为原来的2倍得到的图象对应的函数解析式是________．
答案 y＝sin eq \f(1,2)x
解析 根据函数图象变换法则可得．
4．如图，某地一天从6～14时的温度变化曲线近似满足函数y＝Asin(ωx＋φ)＋b,0