

新高考数学一轮复习学案 第8章 §8.7 抛物线(含解析)
展开1.抛物线的概念
(1)定义:平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹.
(2)焦点:点F叫做抛物线的焦点.
(3)准线:直线l叫做抛物线的准线.
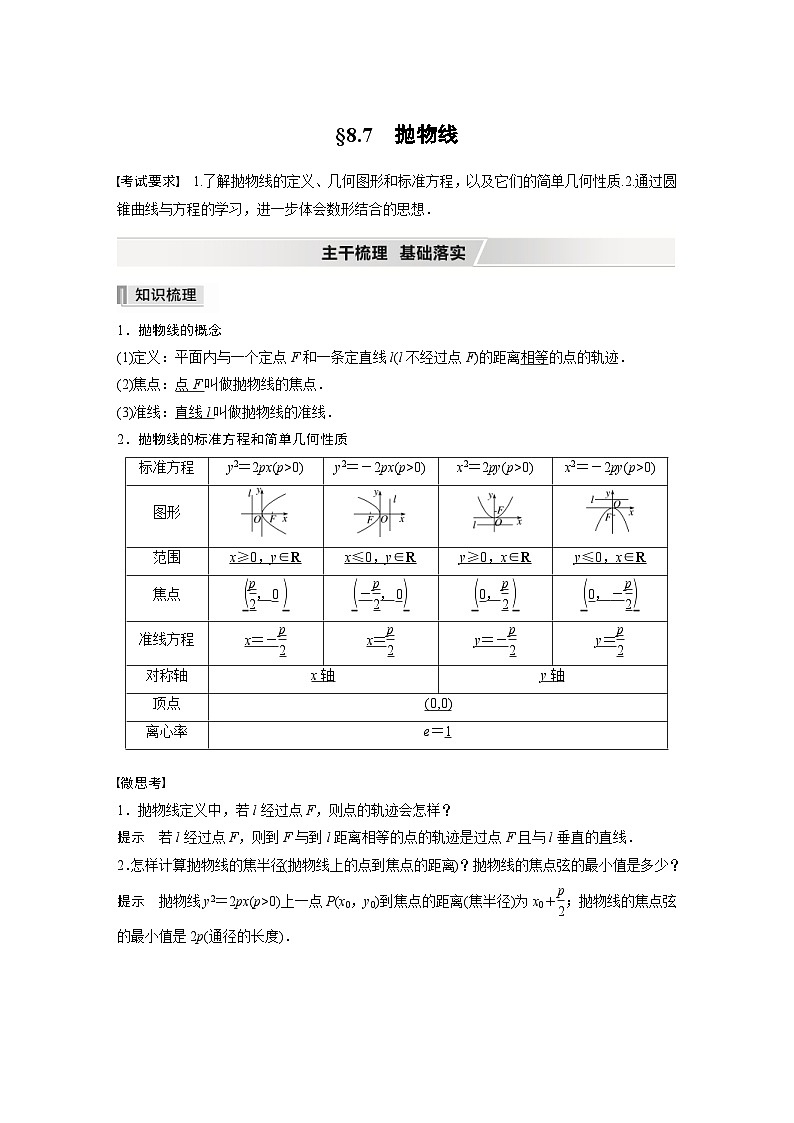
2.抛物线的标准方程和简单几何性质
微思考
1.抛物线定义中,若l经过点F,则点的轨迹会怎样?
提示 若l经过点F,则到F与到l距离相等的点的轨迹是过点F且与l垂直的直线.
2.怎样计算抛物线的焦半径(抛物线上的点到焦点的距离)?抛物线的焦点弦的最小值是多少?
提示 抛物线y2=2px(p>0)上一点P(x0,y0)到焦点的距离(焦半径)为x0+eq \f(p,2);抛物线的焦点弦的最小值是2p(通径的长度).
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线.( × )
(2)方程y=ax2(a≠0)表示的曲线是焦点在x轴上的抛物线,且其焦点坐标是eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a,4),0)),准线方程是x=-eq \f(a,4).( × )
(3)抛物线既是中心对称图形,又是轴对称图形.( × )
(4)若直线与抛物线只有一个交点,则直线与抛物线一定相切.( × )
题组二 教材改编
2.过抛物线y2=4x的焦点的直线l交抛物线于P(x1,y1),Q(x2,y2)两点,如果x1+x2=6,则|PQ|等于( )
A.9 B.8 C.7 D.6
答案 B
解析 抛物线y2=4x的焦点为F(1,0),准线方程为x=-1.根据题意可得,|PQ|=|PF|+|QF|=x1+1+x2+1=x1+x2+2=8.
3.抛物线y2=8x上到其焦点F距离为5的点的个数为______.
答案 2
解析 设P(x1,y1),则|PF|=x1+2=5,得x1=3,y1=±2eq \r(6).故满足条件的点的个数为2.
4.已知A(2,0),B为抛物线y2=x上一点,则|AB|的最小值为________.
答案 eq \f(\r(7),2)
解析 设点B(x,y),则x=y2≥0,
所以|AB|=eq \r(x-22+y2)=eq \r(x-22+x)=eq \r(x2-3x+4)=eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(x-\f(3,2)))2+\f(7,4)).
所以当x=eq \f(3,2)时,|AB|取得最小值,且|AB|min=eq \f(\r(7),2).
题组三 易错自纠
5.(多选)顶点在原点,对称轴为坐标轴且过点P(-2,3)的抛物线的标准方程是( )
A.y2=eq \f(9,2)x B.x2=eq \f(4,3)y
C.y2=-eq \f(9,2)x D.x2=-eq \f(4,3)y
答案 BC
解析 设抛物线的标准方程是y2=kx或x2=my,代入点P(-2,3),解得k=-eq \f(9,2),m=eq \f(4,3),
所以y2=-eq \f(9,2)x或x2=eq \f(4,3)y.
6.设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是______.
答案 [-1,1]
解析 Q(-2,0),当直线l的斜率不存在时,不满足题意,故设直线l的方程为y=k(x+2),代入抛物线方程,消去y整理得k2x2+(4k2-8)x+4k2=0,
由Δ=(4k2-8)2-4k2·4k2=64(1-k2)≥0,
解得-1≤k≤1.
题型一 抛物线的定义和标准方程
1.(2020·全国Ⅰ)已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p等于( )
A.2 B.3 C.6 D.9
答案 C
解析 设A(x,y),由抛物线的定义知,点A到准线的距离为12,即x+eq \f(p,2)=12.
又因为点A到y轴的距离为9,即x=9,
所以9+eq \f(p,2)=12,
解得p=6.
2.设抛物线y2=2px的焦点在直线2x+3y-8=0上,则该抛物线的准线方程为( )
A.x=-4 B.x=-3
C.x=-2 D.x=-1
答案 A
解析 直线2x+3y-8=0与x轴的交点为(4,0),∴抛物线y2=2px的焦点为(4,0),∴准线方程为x=-4.
3.动圆过点(1,0),且与直线x=-1相切,则动圆的圆心的轨迹方程为__________.
答案 y2=4x
解析 设动圆的圆心坐标为(x,y),则圆心到点(1,0)的距离与到直线x=-1的距离相等,根据抛物线的定义易知动圆的圆心的轨迹方程为y2=4x.
4.(2020·佛山模拟)已知抛物线x2=2py(p>0)的焦点为F,准线为l,点P(4,y0)在抛物线上,K为l与y轴的交点,且|PK|=eq \r(2)|PF|,则y0=________,p=________.
答案 2 4
解析 作PM⊥l,垂足为M,由抛物线定义知|PM|=|PF|,又知|PK|=eq \r(2)|PF|,
∴在Rt△PKM中,sin∠PKM=eq \f(|PM|,|PK|)=eq \f(|PF|,|PK|)=eq \f(\r(2),2),
∴∠PKM=45°,∴△PMK为等腰直角三角形,∴|PM|=|MK|=4,又知点P在抛物线x2=2py(p>0)上,
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(py0=8,,y0+\f(p,2)=4,))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(p=4,,y0=2.))
思维升华 (1)应用抛物线定义的两个关键点
①由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.②抛物线焦点到准线的距离为p.
(2)求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置、开口方向,在方程的类型已经确定的前提下,由于标准方程只有一个参数p,只需一个条件就可以确定抛物线的标准方程.
题型二 抛物线的几何性质及应用
命题点1 焦半径和焦点弦
例1 (1)已知抛物线y2=2px(p>0)上横坐标为4的点到此抛物线焦点的距离为9,则该抛物线的焦点到准线的距离为( )
A.4 B.9
C.10 D.18
答案 C
解析 抛物线y2=2px的焦点为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2),0)),准线方程为x=-eq \f(p,2).
由题意可得4+eq \f(p,2)=9,解得p=10,
所以该抛物线的焦点到准线的距离为10.
(2)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为( )
A.eq \f(3\r(3),4) B.eq \f(9\r(3),8) C.eq \f(63,32) D.eq \f(9,4)
答案 D
解析 由已知得焦点坐标为Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,4),0)),
因此直线AB的方程为y=eq \f(\r(3),3)eq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(3,4))),即4x-4eq \r(3)y-3=0.
方法一 联立直线方程与抛物线方程化简得4y2-12eq \r(3)y-9=0,Δ>0显然成立,
则yA+yB=3eq \r(3),yAyB=-eq \f(9,4),
故|yA-yB|=eq \r(yA+yB2-4yAyB)=6.
因此S△OAB=eq \f(1,2)|OF||yA-yB|=eq \f(1,2)×eq \f(3,4)×6=eq \f(9,4).
方法二 联立直线方程与抛物线方程得x2-eq \f(21,2)x+eq \f(9,16)=0,
Δ>0显然成立,故xA+xB=eq \f(21,2).
根据抛物线的定义有|AB|=xA+xB+p=eq \f(21,2)+eq \f(3,2)=12,
同时原点到直线AB的距离为d=eq \f(|-3|,\r(42+-4\r(3)2))=eq \f(3,8),
因此S△OAB=eq \f(1,2)|AB|·d=eq \f(9,4).
命题点2 与抛物线有关的最值问题
例2 (1)已知抛物线y2=4x,过焦点F的直线与抛物线交于A,B两点,过A,B分别作y轴的垂线,垂足分别为C,D,则|AC|+|BD|的最小值为________.
答案 2
解析 由题意知F(1,0),|AC|+|BD|=|AF|+|FB|-2=|AB|-2,即|AC|+|BD|取得最小值时当且仅当|AB|取得最小值.依据抛物线定义知,当|AB|为通径,即|AB|=2p=4时为最小值,所以|AC|+|BD|的最小值为2.
(2)设P是抛物线y2=4x上的一个动点,则点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值为________.
答案 eq \r(5)
解析 如图,易知抛物线的焦点为F(1,0),准线是x=-1,
由抛物线的定义知点P到直线x=-1的距离等于点P到F的距离.
于是,问题转化为在抛物线上求一点P,使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小,
显然,连接AF与抛物线相交的点即为满足题意的点,
此时最小值为eq \r([1--1]2+0-12)=eq \r(5).
思维升华 (1)由抛物线的方程可以确定抛物线的开口方向、焦点位置、焦点到准线的距离,从而进一步确定抛物线的焦点坐标及准线方程.
(2)与抛物线有关的最值问题的两个转化策略
转化策略一:将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”“三角形两边之和大于第三边”,使问题得以解决.
转化策略二:将抛物线上的点到焦点的距离转化为到准线的距离,利用“与直线上所有点的连线中垂线段最短”原理解决.
跟踪训练1 (1)已知抛物线x2=4y上有一条长为6的动弦AB,则AB的中点到x轴的最短距离为( )
A.eq \f(3,4) B.eq \f(3,2) C.1 D.2
答案 D
解析 由题意知,抛物线的准线l:y=-1,过点A作AA1⊥l交l于点A1,过点B作BB1⊥l交l于点B1,设弦AB的中点为M,过点M作MM1⊥l交l于点M1,则|MM1|=eq \f(|AA1|+|BB1|,2).因为|AB|≤|AF|+|BF|(F为抛物线的焦点),即|AF|+|BF|≥6,所以|AA1|+|BB1|≥6,2|MM1|≥6,|MM1|≥3,故点M到x轴的距离d≥2,故选D.
(2)若抛物线y2=4x的准线为l,P是抛物线上任意一点,则P到准线l的距离与P到直线3x+4y+7=0的距离之和的最小值是( )
A.2 B.eq \f(13,5) C.eq \f(14,5) D.3
答案 A
解析 由抛物线定义可知点P到准线l的距离等于点P到焦点F的距离,由抛物线y2=4x及直线方程3x+4y+7=0可得直线与抛物线相离.∴点P到准线l的距离与点P到直线3x+4y+7=0的距离之和的最小值为点F(1,0)到直线3x+4y+7=0的距离,即eq \f(|3+7|,\r(32+42))=2.故选A.
题型三 直线与抛物线
例3 (2021·湖州模拟)如图,已知抛物线x2=y,点Aeq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2),\f(1,4))),Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2),\f(9,4))),抛物线上的点P(x,y)eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2)
(2)求|PA|·|PQ|的最大值.
解 (1)设直线AP的斜率为k,
k=eq \f(x2-\f(1,4),x+\f(1,2))=x-eq \f(1,2),
因为-eq \f(1,2)
(2)联立直线AP与BQ的方程
eq \b\lc\{\rc\ (\a\vs4\al\c1(kx-y+\f(1,2)k+\f(1,4)=0,,x+ky-\f(9,4)k-\f(3,2)=0,))
解得点Q的横坐标是xQ=eq \f(-k2+4k+3,2k2+1).
因为|PA|=eq \r(1+k2)eq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(1,2)))=eq \r(1+k2)(k+1),
|PQ|=eq \r(1+k2)(xQ-x)=-eq \f(k-1k+12,\r(k2+1)),
所以|PA|·|PQ|=-(k-1)(k+1)3.
令f(k)=-(k-1)(k+1)3,因为f′(k)=-(4k-2)(k+1)2,
所以f(k)在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(-1,\f(1,2)))上单调递增,eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),1))上单调递减,
因此当k=eq \f(1,2)时,|PA|·|PQ|取得最大值eq \f(27,16).
思维升华 (1)求解直线与抛物线问题,一般利用方程法,但涉及抛物线的弦长、中点、距离等问题时,要注意“设而不求”“整体代入”“点差法”以及定义的灵活应用.
(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点(设焦点在x轴的正半轴上),可直接使用公式|AB|=x1+x2+p,若不过焦点,则可用弦长公式.
跟踪训练2 (1)(2020·济南期末)直线y=x+b交抛物线y=eq \f(1,2)x2于A,B两点,O为抛物线顶点,OA⊥OB,则b的值为( )
A.-1 B.0 C.1 D.2
答案 D
解析 设A(x1,y1),B(x2,y2),将y=x+b代入y=eq \f(1,2)x2,化简可得x2-2x-2b=0,故x1+x2=2,x1x2=-2b,所以y1y2=x1x2+b(x1+x2)+b2=b2.又OA⊥OB,所以x1x2+y1y2=0,即-2b+b2=0,则b=2或b=0,经检验b=0时,不符合题意,故b=2.
(2)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( )
A.16 B.14 C.12 D.10
答案 A
解析 抛物线C:y2=4x的焦点为F(1,0),由题意可知l1,l2的斜率存在且不为0.不妨设直线l1的斜率为k,则直线l2的斜率为-eq \f(1,k),故l1:y=k(x-1),
l2:y=-eq \f(1,k)(x-1).
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y2=4x,,y=kx-1,))消去y得k2x2-(2k2+4)x+k2=0.
设A(x1,y1),B(x2,y2),∴x1+x2=eq \f(2k2+4,k2)=2+eq \f(4,k2),
由抛物线定义可知,|AB|=x1+x2+2=4+eq \f(4,k2).
同理得|DE|=4+4k2,
∴|AB|+|DE|=8+4k2+eq \f(4,k2)≥8+2eq \r(16)=16.
当且仅当eq \f(1,k2)=k2,即k=±1时取等号.
故|AB|+|DE|的最小值为16.
课时精练
1.(2019·全国Ⅱ)若抛物线y2=2px(p>0)的焦点是椭圆eq \f(x2,3p)+eq \f(y2,p)=1的一个焦点,则p等于( )
A.2 B.3 C.4 D.8
答案 D
解析 由题意知,抛物线的焦点坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2),0)),椭圆的焦点坐标为(±eq \r(2p),0),所以eq \f(p,2)=eq \r(2p),解得p=8,故选D.
2.(2020·全国Ⅲ)设O为坐标原点,直线x=2与抛物线C:y2=2px(p>0)交于D,E两点,若OD⊥OE,则C的焦点坐标为( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4),0)) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),0)) C.(1,0) D.(2,0)
答案 B
解析 方法一 ∵抛物线C关于x轴对称,
∴D,E两点关于x轴对称.
可得出直线x=2与抛物线的两交点的坐标分别为(2,2eq \r(p)),(2,-2eq \r(p)).
不妨设D(2,2eq \r(p)),E(2,-2eq \r(p)),
则eq \(OD,\s\up6(→))=(2,2eq \r(p)),eq \(OE,\s\up6(→))=(2,-2eq \r(p)).
又∵OD⊥OE,
∴eq \(OD,\s\up6(→))·eq \(OE,\s\up6(→))=4-4p=0,解得p=1,
∴C的焦点坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),0)).
方法二 ∵抛物线C关于x轴对称,
∴D,E两点关于x轴对称.
∵OD⊥OE,∴D,E两点横、纵坐标的绝对值均相等.
不妨设点D(2,2),将点D的坐标代入C:y2=2px,
得4=4p,解得p=1,故C的焦点坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),0)).
3.中国古代桥梁的建筑艺术,有不少是世界桥梁史上的创举,充分显示了中国劳动人民的非凡智慧.一个抛物线型拱桥,当水面离拱顶2 m时,水面宽8 m.若水面下降1 m,则水面宽度为( )
A.2eq \r(6) m B.4eq \r(6) m C.4eq \r(2) m D.12 m
答案 B
解析 由题意,以拱桥顶点为原点,建立平面直角坐标系,
设抛物线方程为x2=-2py(p>0),
由题意知,抛物线经过点A(-4,-2)和点B(4,-2),
代入抛物线方程解得p=4,
所以抛物线方程为x2=-8y,
水面下降1米,即y=-3,解得x1=2eq \r(6),x2=-2eq \r(6),
所以此时水面宽度d=2x1=4eq \r(6).
4.(2020·北京)设抛物线的顶点为O,焦点为F,准线为l.P是抛物线上异于O的一点,过P作PQ⊥l于Q,则线段FQ的垂直平分线( )
A.经过点O B.经过点P
C.平行于直线OP D.垂直于直线OP
答案 B
解析 如图所示,P为抛物线上异于O的一点,
则|PF|=|PQ|,
∴QF的垂直平分线经过点P.
5.(多选)设抛物线y=ax2(a>0)的准线与对称轴交于点P,过点P作抛物线的两条切线,切点分别为A和B,则( )
A.点P的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(0,-\f(1,4a)))
B.直线AB的方程为y=eq \f(1,4a)
C.PA⊥PB
D.|AB|=eq \f(1,2a)
答案 ABC
解析 由y=ax2得,x2=eq \f(1,a)y,则焦点Feq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(1,4a))).
∵a>0,∴2p=eq \f(1,a),∴p=eq \f(1,2a),
其准线方程为y=-eq \f(1,4a),∴Peq \b\lc\(\rc\)(\a\vs4\al\c1(0,-\f(1,4a))),A正确;
设切线方程为y=kx-eq \f(1,4a)(k≠0),由eq \b\lc\{\rc\ (\a\vs4\al\c1(y=ax2,,y=kx-\f(1,4a),))
得ax2-kx+eq \f(1,4a)=0,
令Δ=k2-4×a×eq \f(1,4a)=0,解得k=±1.
∴设切点Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2a),\f(1,4a))),Beq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2a),\f(1,4a))),
因此直线AB的方程为y=eq \f(1,4a),B正确;
又eq \(PA,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2a),\f(1,2a))),eq \(PB,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2a),\f(1,2a))),
∴eq \(PA,\s\up6(→))·eq \(PB,\s\up6(→))=-eq \f(1,4a2)+eq \f(1,4a2)=0.
从而eq \(PA,\s\up6(→))⊥eq \(PB,\s\up6(→)),即PA⊥PB,C正确;
|AB|=eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(1,2a)-\b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2a)))))=eq \f(1,a),D错误.
6.(多选)已知抛物线C:y2=2px(p>0)的焦点为F,斜率为eq \r(3)且经过点F的直线l与抛物线C交于A,B两点(点A在第一象限),与抛物线的准线交于点D,若|AF|=4,则以下结论正确的是( )
A.p=2 B.F为AD的中点
C.|BD|=2|BF| D.|BF|=2
答案 ABC
解析 如图.
Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2),0)),直线l的斜率为eq \r(3),
则直线l的方程为y=eq \r(3)eq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(p,2))),
联立eq \b\lc\{\rc\ (\a\vs4\al\c1(y2=2px,,y=\r(3)\b\lc\(\rc\)(\a\vs4\al\c1(x-\f(p,2))),))
得12x2-20px+3p2=0.
解得xA=eq \f(3,2)p,xB=eq \f(1,6)p,
由|AF|=eq \f(3,2)p+eq \f(p,2)=2p=4,得p=2.
∴抛物线方程为y2=4x.
xB=eq \f(1,6)p=eq \f(1,3),
则|BF|=eq \f(1,3)+1=eq \f(4,3);
|BD|=eq \f(|BF|,cs 60°)=eq \f(\f(4,3),\f(1,2))=eq \f(8,3),
∴|BD|=2|BF|,
|BD|+|BF|=eq \f(8,3)+eq \f(4,3)=4,则F为AD的中点.
故选ABC.
7.(2020·新高考全国Ⅰ)斜率为eq \r(3)的直线过抛物线C:y2=4x的焦点,且与C交于A,B两点,则|AB|=________.
答案 eq \f(16,3)
解析 如图,由题意得,抛物线焦点为F(1,0),
设直线AB的方程为y=eq \r(3)(x-1).
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y=\r(3)x-1,,y2=4x,))
得3x2-10x+3=0.
设A(x1,y1),B(x2,y2),
则x1+x2=eq \f(10,3),所以|AB|=x1+x2+2=eq \f(16,3).
8.已知直线l是抛物线y2=2px(p>0)的准线,半径为3的圆过抛物线顶点O和焦点F与l相切,则抛物线的方程为________.
答案 y2=8x
解析 ∵半径为3的圆与抛物线的准线l相切,
∴圆心到准线的距离等于3,
又∵圆心在OF的垂直平分线上,|OF|=eq \f(p,2),
∴eq \f(p,2)+eq \f(p,4)=3,∴p=4,故抛物线的方程为y2=8x.
9.直线l过抛物线C:y2=2px (p > 0)的焦点F(1,0),且与C交于A,B两点,则p=____,eq \f(1,|AF|)+eq \f(1,|BF|)=________.
答案 2 1
解析 由题意知eq \f(p,2)=1,从而p=2,
所以抛物线方程为y2=4x.
当直线AB的斜率不存在时,将x=1代入抛物线方程,解得|AF|=|BF|=2,
从而eq \f(1,|AF|)+eq \f(1,|BF|)=1.
当直线AB的斜率存在时,设AB的方程为y=k(x-1),
联立eq \b\lc\{\rc\ (\a\vs4\al\c1(y=kx-1,,y2=4x,))
整理,得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(x1+x2=\f(2k2+4,k2),,x1x2=1,))
从而eq \f(1,|AF|)+eq \f(1,|BF|)=eq \f(1,x1+1)+eq \f(1,x2+1)=eq \f(x1+x2+2,x1+x2+x1x2+1)=eq \f(x1+x2+2,x1+x2+2)=1.
综上,eq \f(1,|AF|)+eq \f(1,|BF|)=1.
10.点P为抛物线y2=4x上的动点,点A(2,1)为平面内定点,F为抛物线焦点,则:
(1)|PA|+|PF|的最小值为________;
(2)|PA|-|PF|的最小值为________,最大值为________.
答案 (1)3 (2)-eq \r(2) eq \r(2)
解析 (1)如图1,由抛物线定义可知,|PF|=|PH|,|PA|+|PF|=|PA|+|PH|,从而最小值为A到准线的距离为3.
(2)如图2,当P,A,F三点共线,且P在FA延长线上时,|PA|-|PF|有最小值为-|AF|=-eq \r(2).当P,A,F三点共线,且P在AF延长线上时,|PA|-|PF|有最大值为|AF|=eq \r(2).故|PA|-|PF|的最小值为-eq \r(2),最大值为eq \r(2).
11.定长为3的线段AB的端点A,B在抛物线y2=x上移动,求AB的中点到y轴距离的最小值,并求出此时AB中点的坐标.
解 如图所示,F是抛物线y2=x的焦点,
过A,B两点作准线的垂线,垂足分别为C,D,
过AB的中点M作准线的垂线MN,垂足为N,
则|MN|=eq \f(1,2)(|AC|+|BD|).
连接AF,BF,由抛物线的定义知|AC|=|AF|,|BD|=|BF|,
所以|MN|=eq \f(1,2)(|AF|+|BF|)≥eq \f(1,2)|AB|=eq \f(3,2).
设点M的横坐标为x,则|MN|=x+eq \f(1,4),
所以x≥eq \f(3,2)-eq \f(1,4)=eq \f(5,4).
当弦AB过点F时等号成立,
此时,点M到y轴的距离最短,最短距离为eq \f(5,4).
设A(x1,y1),B(x2,y2),则x1+x2=2x.
当x=eq \f(5,4)时,易知y1y2=-p2=-eq \f(1,4),
所以(y1+y2)2=yeq \\al(2,1)+yeq \\al(2,2)+2y1y2=2x-eq \f(1,2)=2.
所以y1+y2=±eq \r(2),得y=±eq \f(\r(2),2),即Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,4),±\f(\r(2),2))).
12.(2021·沈阳模拟)已知抛物线C:x2=2py(p>0),其焦点到准线的距离为2,直线l与抛物线C交于A,B两点,过A,B分别作抛物线C的切线l1,l2,且l1与l2交于点M.
(1)求p的值;
(2)若l1⊥l2,求△MAB面积的最小值.
解 (1)由题意知,抛物线焦点为eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(p,2))),
准线方程为y=-eq \f(p,2),
焦点到准线的距离为2,即p=2.
(2)由(1)知抛物线的方程为x2=4y,
即y=eq \f(1,4)x2,所以y′=eq \f(1,2)x,
设A(x1,y1),B(x2,y2),
l1:y-eq \f(x\\al(2,1),4)=eq \f(x1,2)(x-x1),
l2:y-eq \f(x\\al(2,2),4)=eq \f(x2,2)(x-x2),
由于l1⊥l2,所以eq \f(x1,2)·eq \f(x2,2)=-1,
即x1x2=-4.
设直线l的方程为y=kx+m,与抛物线方程联立,
得eq \b\lc\{\rc\ (\a\vs4\al\c1(y=kx+m,,x2=4y,))
所以x2-4kx-4m=0,Δ=16k2+16m>0,
x1+x2=4k,x1x2=-4m=-4,所以m=1,即l:y=kx+1.
联立方程eq \b\lc\{\rc\ (\a\vs4\al\c1(y=\f(x1,2)x-\f(x\\al(2,1),4),,y=\f(x2,2)x-\f(x\\al(2,2),4),))得eq \b\lc\{\rc\ (\a\vs4\al\c1(x=2k,,y=-1,))即M(2k,-1).
M点到直线l的距离d=eq \f(|k·2k+1+1|,\r(1+k2))=eq \f(2|k2+1|,\r(1+k2)),
|AB|=eq \r(1+k2[x1+x22-4x1x2])=4(1+k2),
所以S=eq \f(1,2)×4(1+k2)×eq \f(2|k2+1|,\r(1+k2))= SKIPIF 1 < 0 ≥4,
当k=0时,△MAB的面积取得最小值4.
13.抛物线x2=4y的焦点为F,过点F作斜率为eq \f(\r(3),3)的直线l与抛物线在y轴右侧的部分相交于点A,过点A作抛物线准线的垂线,垂足为H,则△AHF的面积是( )
A.4 B.3eq \r(3) C.4eq \r(3) D.8
答案 C
解析 由抛物线的定义可得|AF|=|AH|,
∵AF的斜率为eq \f(\r(3),3),∴直线AF的倾斜角为30°,
∵AH垂直于准线,∴∠FAH=60°,
故△AHF为等边三角形.
设Aeq \b\lc\(\rc\)(\a\vs4\al\c1(m,\f(m2,4))),m>0,
过F作FM⊥AH于M,则在Rt△FAM中,
|AM|=eq \f(1,2)|AF|,∴eq \f(m2,4)-1=eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(m2,4)+1)),
解得m=2eq \r(3),故等边三角形AHF的边长|AH|=4,
∴△AHF的面积是eq \f(1,2)×4×4sin 60°=4eq \r(3).故选C.
14.过抛物线C:x2=4y的焦点F作直线l交C于A,B两点,设D(0,3).若(eq \(DA,\s\up6(→))+eq \(DB,\s\up6(→)))·eq \(AB,\s\up6(→))=0,则弦AB的长为________.
答案 4
解析 若(eq \(DA,\s\up6(→))+eq \(DB,\s\up6(→)))·eq \(AB,\s\up6(→))=0,
则线段AB的垂直平分线过点D.
设A(x1,y1),B(x2,y2),
则xeq \\al(2,1)=4y1,xeq \\al(2,2)=4y2,
两式相减得x1+x2=eq \f(4y1-y2,x1-x2)=4kAB,
即kAB=eq \f(x1+x2,4),
则弦AB的中点与点D(0,3)的连线的斜率k=eq \f(\f(y1+y2,2)-3,\f(x1+x2,2))=-eq \f(4,x1+x2),
所以y1+y2=2,
所以|AB|=y1+y2+2=4.
15.(2020·湖南名校大联考)已知P为抛物线C:y=x2上一动点,直线l:y=2x-4与x轴、 y轴交于M,N两点,点A(2,-4)且eq \(AP,\s\up6(→))=λeq \(AM,\s\up6(→))+μeq \(AN,\s\up6(→)),则λ+μ的最小值为________.
答案 eq \f(7,4)
解析 由题意得M(2,0),N(0,-4),
设P(x,y),由eq \(AP,\s\up6(→))=λeq \(AM,\s\up6(→))+μeq \(AN,\s\up6(→))得(x-2,y+4)=λ(0,4)+μ(-2,0),
∴x-2=-2μ,y+4=4λ.
因此λ+μ=eq \f(y+4,4)-eq \f(x-2,2)=eq \f(x2,4)-eq \f(x,2)+2=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,2)-\f(1,2)))2+eq \f(7,4)≥eq \f(7,4),故λ+μ的最小值为eq \f(7,4).
16.过抛物线y2=2px(p>0)的焦点F作一条倾斜角为eq \f(π,4)的直线与抛物线相交于A,B两点.
(1)用p表示A,B之间的距离;
(2)证明:∠AOB的大小是与p无关的定值,并求出这个值.
解 (1)焦点Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2),0)),过点F且倾斜角为eq \f(π,4)的直线方程是y=x-eq \f(p,2).
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y2=2px,,y=x-\f(p,2),))得x2-3px+eq \f(p2,4)=0.
设A(xA,yA),B(xB,yB),则xA+xB=3p,xAxB=eq \f(p2,4),
故|AB|=xA+xB+p=4peq \b\lc\(\rc\)(\a\vs4\al\c1(或|AB|=\f(2p,sin2\f(π,4))=4p)).
(2)在△AOB中,由余弦定理可知,
cs∠AOB=eq \f(|AO|2+|BO|2-|AB|2,2|AO|·|BO|)=eq \f(x\\al(2,A)+y\\al(2,A)+x\\al(2,B)+y\\al(2,B)-xA-xB2-yA-yB2,2\r(x\\al(2,A)+y\\al(2,A)x\\al(2,B)+y\\al(2,B)))
=eq \f(xAxB+yAyB,\r(x\\al(2,A)+y\\al(2,A)x\\al(2,B)+y\\al(2,B)))=eq \f(2xAxB-\f(p,2)xA+xB+\f(p2,4),\r(xAxB[xAxB+2pxA+xB+4p2]))=-eq \f(3\r(41),41).
即∠AOB的大小是与p无关的定值,
且cs∠AOB=-eq \f(3\r(41),41).标准方程
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
图形
范围
x≥0,y∈R
x≤0,y∈R
y≥0,x∈R
y≤0,x∈R
焦点
eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2),0))
eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(p,2),0))
eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(p,2)))
eq \b\lc\(\rc\)(\a\vs4\al\c1(0,-\f(p,2)))
准线方程
x=-eq \f(p,2)
x=eq \f(p,2)
y=-eq \f(p,2)
y=eq \f(p,2)
对称轴
x轴
y轴
顶点
(0,0)
离心率
e=1
2025年高考数学一轮复习-8.7-抛物线【导学案】: 这是一份2025年高考数学一轮复习-8.7-抛物线【导学案】,共34页。
2025年高考数学一轮复习-8.7-抛物线【导学案】: 这是一份2025年高考数学一轮复习-8.7-抛物线【导学案】,共34页。
(新高考)高考数学一轮复习学案9.7《抛物线》(含详解): 这是一份(新高考)高考数学一轮复习学案9.7《抛物线》(含详解),共15页。学案主要包含了知识梳理,教材衍化等内容,欢迎下载使用。












