华师2024版数学七年级上册 第四章 第4章归纳总结 PPT课件

这是一份华师2024版数学七年级上册 第4章 第四章归纳总结 PPT课件，共26页。

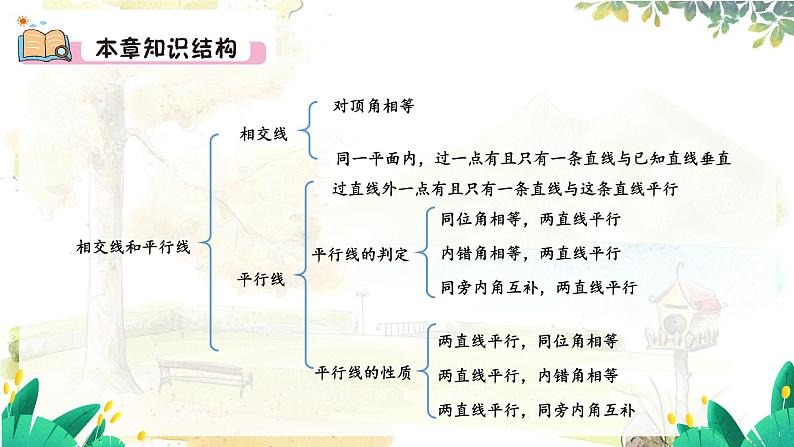
第四章 相交线和平行线 归纳总结华师版 七年级 上册相交线和平行线相交线对顶角相等同一平面内，过一点有且只有一条直线与已知直线垂直平行线过直线外一点有且只有一条直线与这条直线平行平行线的判定同位角相等，两直线平行内错角相等，两直线平行同旁内角互补，两直线平行平行线的性质两直线平行，同位角相等两直线平行，内错角相等两直线平行，同旁内角互补本章回顾1.对顶角：有一个公共顶点，且一个角的两边分别是另一个角的两边的反向 延长线，这样的两个角互为对顶角.（如图中∠1和∠2）对顶角的性质：对顶角相等.注意：（1）对顶角是成对出现的，对顶角是具有特殊位置关系的两个角；（2）如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角.2.邻补角：两条直线相交所形成的4个角中，有公共点且有一条公共边的两个角是邻补角（如图中∠1和∠2）邻补角的性质：同角的补角相等.∠1和∠2互补， ∠1和∠4互补所以∠2= ∠4（同角的补角相等）3.垂线性质：①过一点有且只有一条直线与已知直线垂直；②垂线段最短.（1）垂线与垂线段区别：垂线是一条直线，不可度量长度；垂线段是一条线段，可以度量长度.联系：具有垂直于已知直线的共同特征 (垂直的性质).（2）两点间距离与点到直线的距离区别：两点间的距离是点与点之间，点到直线的距离是点与直线之间.联系：都是线段的长度；点到直线的距离是特殊的两点(即已知点与垂足)间距离.4.平行线的概念在同一平面内，不相交的两条直线叫做平行线，直线 a 与直线 b 互相平行，记作 a∥ b.在同一平面内，不重合的两条直线的位置关系有两种： ①相交；②平行.（2）判断同一平面内两直线的位置关系时，可以根据它们的公共点的个数来确定：①有且只有一个公共点，两直线相交；②无公共点，则两直线平行；③两个或两个以上公共点，则两直线重合（因为两点确定一条直线）.5.平行公理的推论如果两条直线都与第三条直线平行，那么这两条直线也互相平行.注意：（1）平行公理中的“有且只有”包含两层意思：一是存在性；二是唯一性.（2）平行具有传递性，即如果 a∥ b，b∥ c，则 a∥ c.6.如何判别同位角、内错角、同旁内角方法：判别同位角、内错角或同旁内角的关键是找到构成这两个角的“三线”，有时需要将有关的部分“抽出”或把无关的线略去不看，有时又需要把图形补全.如图，判断下列各对角的位置关系：(1)∠1与∠2；(2)∠1与∠7；(3)∠1与∠BAD；(4)∠2与∠6；(5)∠5与∠8.∠5与∠8对顶角.∠1与∠2是同旁内角；∠1与∠7是同位角；∠1与∠BAD是同旁内角；∠2与∠6是内错角；（1）同位角相等，两直线平行（在同一平面内）；（2）内错角相等，两直线平行（在同一平面内）；（3）同旁内角互补，两直线平行（在同一平面内）；（4）如果两条直线都和第三条直线平行，那么这两条直线也互相平行. 补充：（5）在同一平面内，垂直于同一直线的两直线平行.7.平行线的判定（1）两直线平行，同位角相等（在同一平面内）；（2）两直线平行，内错角相等（在同一平面内）；（3）两直线平行，同旁内角互补（在同一平面内）.8.平行线的性质如图，点A 、B、C在同一条直线上，∠1 = 53°，∠2 = 37°，则 CD 与 CE 垂直吗？CD与CE垂直如图，直线 AB、CD 相交于点 E，∠BEF = 40°，∠CEF = 85°，则 ∠AED =_______°.125如图，直线 AB、CD 相交于点 E，EF 平分 ∠AED，∠DEF = 55°，则 ∠BEC =________°如图，某地为了加快乡村振兴，要从村庄 Р 修一条村道，使村民自村庄 Р 出发到公路的距离最短，试画出这条村道，并说明理由.垂线段最短110如图，经过直线 a 外一点 P 的 4 条直线中，与直线 a 平行的直线是________.PB如图，如果 AB // CD，那么 ∠A 与∠C________.互补如图，如果∠1 =∠3，那么直线 a 与 b 平行吗？当∠2与∠3 满足什么关系时，直线 a 与 b 平行？直线 a 与 b平行满足互补关系时直线 a 与 b 平行8.如图，a、b、c、d均为直线. 如果希望a∥b，那么需要∠1至∠5中哪两个角相等？如果希望c∥d，那么需要∠1至∠5中哪两个角互补？如果a∥ b则∠3=∠4如果c∥ d则∠1与∠4互补9.如图，已知平行直线 a、b 被直线 l 所截. 如果∠1 = 75°，那么∠2=_____°，∠3 =_____°，∠4 =_____°，∠5 =______°，∠6=______°，∠7=____°，∠8=____°.105751057510575105l10.如图，直线 a // b，∠3 = 85°，求 ∠1、∠2 的度数，阅读下面的解答过程，并填空 (理由或数学式). 解 : ∵a // b （ ）， ∴∠1 = ∠4（ ）. ∴∠4 = ∠3（ ）， ∠3 = 85°（ ） ∴ ∠1=（ ）（等量代换）. 又∵∠2 +∠3 = 180°， ∴∠2 =（ ）（等式的性质）.已知两直线平行，同位角相等对顶角相等已知85°95°11.如图，已知 AC⊥AE，BD⊥BF，∠1 = 35°，∠2 = 35°，则 AC 与BD 平行吗？AE 与 BF 平行吗？阅读下面的解答过程，并填空(理由或数学式). 解 ∵∠1 = 35°（ ），∠2 = 35°（ ） ， ∴ ∠1 = ∠2（ ）， ∴（ ）//（ ）（ ）. 又∵ AC⊥ AE（ ）， ∴∠EAC = 90°， ∴∠EAB = ∠EAC+∠1 =（ ）（等式的性质）. 同理可得 ∠FBG = ∠FBD +∠2 =（ ）. ∴∠EAB =（ ）（等量代换）， ∴（ ）//（ ）（ ）.已知等量代换ACBD同位角相等，两直线平行已知125°125°∠FBGAEBF同位角相等，两直线平行已知12.如图，如果 AB // CD，∠B = 37°，∠D = 37°，那么 BC 与 DE 平行吗？阅读下面的解答过程，并填空(理由或数学式). 解: ∵AB // CD（ ） ， ∴∠B = （ ）（ ）. ∵∠B =∠D = 37°（ ）， ∴（ ） = ∠D（ ） ， ∴BC // DE（ ）.已知∠C两直线平行，内错角相等已知∠C等量代换内错角相等，两直线平行13.如图，我们知道，2 条直线相交只有 1 个交点，3 条直线两两相交最多能有 3 个交点，4 条直线两两相交最多能有 6 个交点，5 条直线两两相交最多能有 10 个交点，6 条直线两两相交最多能有 15 个交点……n 条直线两两相交呢？14.潜望镜中，两面镜子互相平行放置. 你知道为什么进入潜望镜的光线和离开潜望镜的光线平行吗？所以两条光线平行（内错角相等，两直线平行）解： ∵∠2=∠3（两直线平行，内错角相等）∵∠1=∠2，∠3=∠4∴∠1=∠2=∠3=∠4∵∠5=180°-∠1-∠2∠6=180°-∠3-∠4∴∠5=∠615.如果一个角的两边与另一个角的两边互相平行，那么这两个角的大小有什么关系呢?此时，小红首先想到如图所示的图形．她发现这两个角应该相等.你知道其中的原因吗?你是否还能发现其他图形呢?画出所有可能的情况，探究归纳你所得到的结论.∴ ∠B=∠E∴ ∠B + ∠PMN=180°（1） ∵ AB∥ DE∴ ∠B = ∠DGC∵ BC∥ EF∴ ∠DGC = ∠E（2） ∵ AB∥ PM∴ ∠B + ∠BOP=180°∵ BC∥ MN∴∠PMN = ∠BOP相等互补（3）相等结论:如果一个角的两边与另一个角的两边互相平行,那么这两个角相等或互补.（4）互补1.从课后习题中选取；2.完成练习册本课时的习题。课后作业