2021-2022学年江苏省盐城市滨海县八年级上学期期中数学试题及答案

这是一份2021-2022学年江苏省盐城市滨海县八年级上学期期中数学试题及答案，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）现实世界中，对称现象无处不在，中国的方块字中有些也具备对称性，下列汉字不是轴对称图形的是（ ）
A．一B．中C．王D．语
2．（3分）下列各组数分别为一个三角形三边的长，其中能构成直角三角形的一组是（ ）
A．2，3，4B．6，8，10C．5，12，14D．1，1，2
3．（3分）如图，△ABC≌△ADE，若∠B＝80°，∠C＝30°，则∠E的度数为（ ）
A．80°B．35°C．70°D．30°
4．（3分）如图，在△ABC中，∠B＝36°，AB＝AC，AD是△ABC的中线，则∠BAD的度数是（ ）
A．36°B．54°C．72°D．108°
5．（3分）如图，在△ABC中，∠C＝90°，AC＝4，BC＝2．以AB为一条边向三角形外部作正方形，则正方形的面积是（ ）
A．8B．12C．18D．20
6．（3分）如图所示，公路AC、BC互相垂直，点M为公路AB的中点，为测量湖泊两侧C、M两点间的距离，若测得AB的长为6km，则M、C两点间的距离为（ ）
A．2.5kmB．4.5kmC．5kmD．3km
7．（3分）下列说法正确的是（ ）
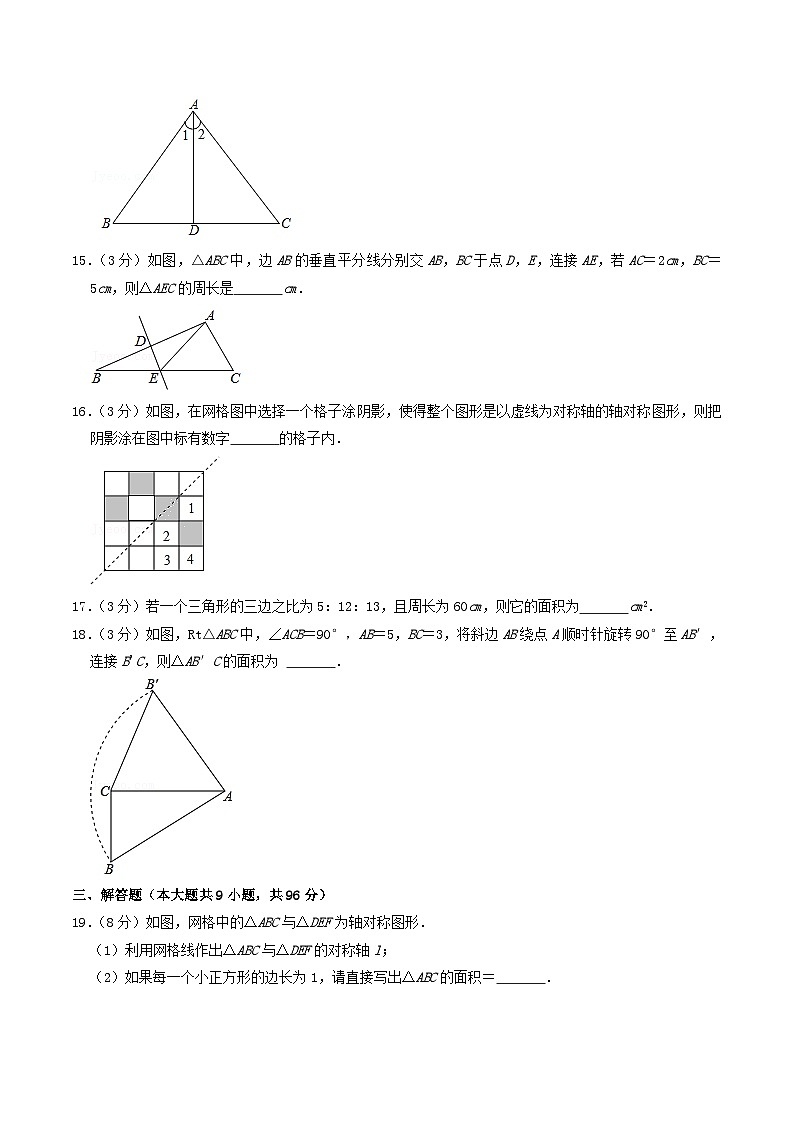
A．两个全等图形面积一定相等
B．两个等边三角形一定是全等图形
C．形状相同的两个图形一定全等
D．两个正方形一定是全等图形
8．（3分）如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3＝（ ）
A．90°B．135°C．150°D．180°
二、填空题（本大题共10小题，每小题3分，共30分.请把答案填写在答题卡相应位置.）
9．（3分）用一根长12cm的铁丝围成一个等边三角形，那么这个等边三角形的边长为 cm．
10．（3分）在△ABC中，AB＝AC，∠A＝40°，则∠B的度数为 °．
11．（3分）木工师傅要做扇长方形纱窗，做好后量得长为6分米，宽为4分米，对角线为7分米，则这扇纱窗 （填“合格”或“不合格”）．
12．（3分）若（a﹣4）2+|b﹣2|＝0，则有两边长为a、b的等腰三角形的周长为 ．
13．（3分）如图，A、F、C、D在同一条直线上，△ABC≌△DEF，AF＝1，FD＝3．则线段FC的长为 ．
14．（3分）如图，△ABC中，AB＝AC，∠1＝∠2，BC＝6cm，那么BD的长 cm．
15．（3分）如图，△ABC中，边AB的垂直平分线分别交AB，BC于点D，E，连接AE，若AC＝2cm，BC＝5cm，则△AEC的周长是 cm．
16．（3分）如图，在网格图中选择一个格子涂阴影，使得整个图形是以虚线为对称轴的轴对称图形，则把阴影涂在图中标有数字 的格子内．
17．（3分）若一个三角形的三边之比为5：12：13，且周长为60cm，则它的面积为 cm2．
18．（3分）如图，Rt△ABC中，∠ACB＝90°，AB＝5，BC＝3，将斜边AB绕点A顺时针旋转90°至AB′，连接B'C，则△AB′C的面积为 ．
三、解答题（本大题共9小题，共96分）
19．（8分）如图，网格中的△ABC与△DEF为轴对称图形．
（1）利用网格线作出△ABC与△DEF的对称轴l；
（2）如果每一个小正方形的边长为1，请直接写出△ABC的面积＝ ．
20．（10分）已知：如图，若AB∥CD，AB＝CD且BE＝CF．求证：AE＝DF．
21．（10分）已知：如图，∠A＝∠D＝90°，点E、F在线段BC上，DE与AF交于点O，且AB＝CD，BE＝CF．求证：△OEF是等腰三角形．
22．（10分）如图，厂房屋顶的人字架是等腰三角形，AB＝AC，AD⊥BC，若跨度BC＝16m，上弦长AB＝10m，求中柱AD的长．
23．（10分）如图，△ABC中，BC的垂直平分线DE分别交AB、BC于点D、E，且BD2﹣DA2＝AC2．
（1）求证：∠A＝90°；
（2）若AB＝8，AD：BD＝3：5，求AC的长．
24．（10分）如图，把一块等腰直角三角形零件（△ABC，其中∠ACB＝90°），放置在一凹槽内，三个顶点A，B，C分别落在凹槽内壁上，已知∠ADE＝∠BED＝90°，测得AD＝5cm，BE＝7cm，求该三角形零件的面积．
25．（12分）如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高．
（1）求证：AD垂直平分EF；
（2）若AB+AC＝10，S△ABC＝15，求DE的长．
26．（12分）如图，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝CD．
（1）证明：△BCE≌△DCF；
（2）若AB＝21，AD＝9，BC＝CD＝10，求AC的长．
27．（14分）如图，在等边△ABC中，AB＝AC＝BC＝6cm，现有两点M、N分别从点A、B同时出发，沿三角形的边运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次回到点B时，点M、N同时停止运动，设运动时间为ts．
（1）当t为何值时，M、N两点重合；
（2）当点M、N分别在AC、BA边上运动，△AMN的形状会不断发生变化．
①当t为何值时，△AMN是等边三角形；
②当t为何值时，△AMN是直角三角形；
（3）若点M、N都在BC边上运动，当存在以MN为底边的等腰△AMN时，求t的值．
2021-2022学年江苏省盐城市滨海县八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共8小题，每小题3分，共24分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上.）
1．（3分）现实世界中，对称现象无处不在，中国的方块字中有些也具备对称性，下列汉字不是轴对称图形的是（ ）
A．一B．中C．王D．语
【分析】直接利用轴对称图形的定义得出答案．
【解答】解：A、“一”是轴对称图形，故本选项不合题意；
B、“中”是轴对称图形，故本选项不合题意；
C、“王”是轴对称图形，故本选项不合题意；
D、“语”不是轴对称图形，故本选项符合题意．
故选：D．
2．（3分）下列各组数分别为一个三角形三边的长，其中能构成直角三角形的一组是（ ）
A．2，3，4B．6，8，10C．5，12，14D．1，1，2
【分析】先求出两小边的平方和，再求出最长边的平方，看看是否相等即可．
【解答】解：A．∵22+32≠42，
∴以2，3，4为边不能组成直角三角形，故本选项不符合题意；
B．∵62+82＝102，
∴以6，8，10为边能组成直角三角形，故本选项符合题意；
C．∵52+122≠142，
∴5，12，14为边不能组成直角三角形，故本选项不符合题意；
D．∵12+12≠22，
∴以1，1，2为边不能组成直角三角形，故本选项不符合题意；
故选：B．
3．（3分）如图，△ABC≌△ADE，若∠B＝80°，∠C＝30°，则∠E的度数为（ ）
A．80°B．35°C．70°D．30°
【分析】根据全等三角形的对应角相等解答即可．
【解答】解：∵△ABC≌△ADE，∠C＝30°，
∴∠E＝∠C＝30°，
故选：D．
4．（3分）如图，在△ABC中，∠B＝36°，AB＝AC，AD是△ABC的中线，则∠BAD的度数是（ ）
A．36°B．54°C．72°D．108°
【分析】根据等腰三角形的性质和垂直的定义即可得到结论．
【解答】解：∵AB＝AC，AD是△ABC的中线，
∴AD⊥BC，
∴∠ADB＝90°，
∵∠B＝36°，
∴∠BAD＝90°﹣36°＝54°，
故选：B．
5．（3分）如图，在△ABC中，∠C＝90°，AC＝4，BC＝2．以AB为一条边向三角形外部作正方形，则正方形的面积是（ ）
A．8B．12C．18D．20
【分析】根据勾股定理和正方形的面积公式即可得到结论．
【解答】解：∵∠C＝90°，AC＝4，BC＝2，
∴AB＝＝＝2，
∴正方形的面积＝AB2＝（2）2＝20，
故选：D．
6．（3分）如图所示，公路AC、BC互相垂直，点M为公路AB的中点，为测量湖泊两侧C、M两点间的距离，若测得AB的长为6km，则M、C两点间的距离为（ ）
A．2.5kmB．4.5kmC．5kmD．3km
【分析】根据直角三角形斜边上的中线性质得出CM＝AB，即可求出CM．
【解答】解：∵公路AC，BC互相垂直，
∴∠ACB＝90°，
∵M为AB的中点，
∴CM＝AB，
∵AB＝6km，
∴CM＝3km，
即M，C两点间的距离为3km，
故选：D．
7．（3分）下列说法正确的是（ ）
A．两个全等图形面积一定相等
B．两个等边三角形一定是全等图形
C．形状相同的两个图形一定全等
D．两个正方形一定是全等图形
【分析】直接利用全等图形的性质以及定义，分别分析得出答案．
【解答】解：A．两个全等图形面积一定相等，故此选项合题意；
B．两个等边三角形不一定是全等图形，故此选项不合题意；
C．形状相同的两个图形不一定全等，故此选项不合题意；
D．两个正方形不一定是全等图形，故此选项不符合题意；
故选：A．
8．（3分）如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3＝（ ）
A．90°B．135°C．150°D．180°
【分析】标注字母，利用“边角边”判断出△ABC和△DEA全等，根据全等三角形对应角相等可得∠1＝∠4，然后求出∠1+∠3＝90°，再判断出∠2＝45°，然后计算即可得解．
【解答】解：如图，在△ABC和△DEA中，
，
∴△ABC≌△DEA（SAS），
∴∠1＝∠4，
∵∠3+∠4＝90°，
∴∠1+∠3＝90°，
又∵∠2＝45°，
∴∠1+∠2+∠3＝90°+45°＝135°．
故选：B．
二、填空题（本大题共10小题，每小题3分，共30分.请把答案填写在答题卡相应位置.）
9．（3分）用一根长12cm的铁丝围成一个等边三角形，那么这个等边三角形的边长为 4 cm．
【分析】等边三角形的三条边相等，用12除以3就得这个三角形的边长，由此可得答案．
【解答】解：12÷3＝4（cm）．
答：这个等边三角形的边长为4cm．
故答案为：4．
10．（3分）在△ABC中，AB＝AC，∠A＝40°，则∠B的度数为 70 °．
【分析】根据等腰三角形的性质可得到∠B＝∠C，已知顶角的度数，根据三角形内角和定理即可求解．
【解答】解：∵AB＝AC，
∴∠B＝∠C，
∵∠A＝40°，
∴∠B＝（180°﹣40°）÷2＝70°．
故答案为：70．
11．（3分）木工师傅要做扇长方形纱窗，做好后量得长为6分米，宽为4分米，对角线为7分米，则这扇纱窗 不合格 （填“合格”或“不合格”）．
【分析】直接利用勾股定理逆定理分析得出答案．
【解答】解：∵42+62＝52≠72＝49，
∴这扇纱窗不是直角，故不合格．
故答案为：不合格．
12．（3分）若（a﹣4）2+|b﹣2|＝0，则有两边长为a、b的等腰三角形的周长为 10 ．
【分析】先根据非负数的性质列式求出a、b，再根据等腰三角形和三角形三边关系分情况讨论求解即可．
【解答】解：根据题意得，a﹣4＝0，b﹣2＝0，
解得a＝4，b＝2，
①若2是腰长，则底边为4，三角形的三边分别是2，2，4，不能组成三角形；
②若4是腰长，则底边为2，三角形的三边分别是4，4，2，能组成三角形，周长＝4+4+2＝10，
故答案为：10．
13．（3分）如图，A、F、C、D在同一条直线上，△ABC≌△DEF，AF＝1，FD＝3．则线段FC的长为 2 ．
【分析】根据全等三角形的性质得出AC＝FD＝3，再求出FC即可．
【解答】解：∵△ABC≌△DEF，FD＝3，
∴AC＝FD＝3，
∵AF＝1，
∴FC＝AC﹣AF＝3﹣1＝2，
故答案为：2．
14．（3分）如图，△ABC中，AB＝AC，∠1＝∠2，BC＝6cm，那么BD的长 3 cm．
【分析】由AB＝AC，得出△ABC是等腰三角形，由∠1＝∠2，得出AD是顶角平分线，再由等腰三角形底边上的中线与顶角平分线重合求解即可．
【解答】解：∵AB＝AC，
∴△ABC是等腰三角形，
∵∠1＝∠2，
∴BD＝CD＝BC，
∵BC＝6cm，
∴BD＝×6＝3（cm）．
故答案为：3．
15．（3分）如图，△ABC中，边AB的垂直平分线分别交AB，BC于点D，E，连接AE，若AC＝2cm，BC＝5cm，则△AEC的周长是 7 cm．
【分析】根据线段的垂直平分线的性质得到EA＝EB，根据三角形的周长公式计算，得到答案．
【解答】解：∵DE是线段AB的垂直平分线，
∴EA＝EB，
∴△AEC的周长＝AC+EC+EA＝AC+EC+EB＝AC+BC＝7（cm），
故答案为：7．
16．（3分）如图，在网格图中选择一个格子涂阴影，使得整个图形是以虚线为对称轴的轴对称图形，则把阴影涂在图中标有数字 3 的格子内．
【分析】从阴影部分图形的各顶点向虚线作垂线并延长相同的距离找对应点，然后顺次连接各点可得答案．
【解答】解：如图所示，
把阴影涂在图中标有数字3的格子内所组成的图形是轴对称图形，
故答案为：3．
17．（3分）若一个三角形的三边之比为5：12：13，且周长为60cm，则它的面积为 120 cm2．
【分析】根据已知可求得三边的长，再根据三角形的面积公式即可求解．
【解答】解：设三边分别为5x，12x，13x，
则5x+12x+13x＝60，
∴x＝2，
∴三边分别为10cm，24cm，26cm，
∵102+242＝262，
∴三角形为直角三角形，
∴S＝10×24÷2＝120cm2．
故答案为：120．
18．（3分）如图，Rt△ABC中，∠ACB＝90°，AB＝5，BC＝3，将斜边AB绕点A顺时针旋转90°至AB′，连接B'C，则△AB′C的面积为 8 ．
【分析】过点B'作B'H⊥AC于H，由（1）可得：△ACB≌△B'HA（AAS），得AC＝B'H＝4，则有S△AB'C＝AC•B′H＝×4×4＝8．
【解答】解：过点B'作B'H⊥AC于H，
∴∠AHB'＝90°，
∴∠HAB'+∠HB'A＝90°，
∠BAC+∠CAB'＝90°，
∴∠HB'A＝∠ACB，
在△ACB和△B'HA中，
，
∴△ACB≌△B'HA（AAS），
∴AC＝B'H，
∵∠ACB＝90°，AB＝5，BC＝3，
∴AC＝＝＝4，
∴AC＝B'H＝4，
∴S△AB'C＝AC•B′H＝×4×4＝8．
故答案为：8．
三、解答题（本大题共9小题，共96分）
19．（8分）如图，网格中的△ABC与△DEF为轴对称图形．
（1）利用网格线作出△ABC与△DEF的对称轴l；
（2）如果每一个小正方形的边长为1，请直接写出△ABC的面积＝ 3 ．
【分析】（1）对应点连线段的垂直平分线即为对称轴；
（2）把三角形的面积看成矩形面积减去周围三个三角形面积即可．
【解答】解：（1）如图，直线l即为所求；
（2）S△ABC＝2×4﹣×1×2﹣×2×2﹣×1×4＝3，
故答案为：3．
20．（10分）已知：如图，若AB∥CD，AB＝CD且BE＝CF．求证：AE＝DF．
【分析】由AB∥CD，得∠B＝∠C，再利用SAS证明△ABE≌△DCF，从而得出AE＝DF．
【解答】证明：∵AB∥CD，
∴∠B＝∠C，
在△ABE与△DCF中，
，
∴△ABE≌△DCF（SAS），
∴AE＝DF．
21．（10分）已知：如图，∠A＝∠D＝90°，点E、F在线段BC上，DE与AF交于点O，且AB＝CD，BE＝CF．求证：△OEF是等腰三角形．
【分析】证明Rt△ABF≌Rt△DCE，根据全等三角形的性质得到∠AFB＝∠DEC，根据等腰三角形的判定定理证明结论．
【解答】证明：∵BE＝CF，
∴BE+EF＝CF+EF，即BF＝CE，
在Rt△ABF和Rt△DCE中，
，
∴Rt△ABF≌Rt△DCE（HL）
∴∠AFB＝∠DEC，
∴OE＝OF，
∴△OEF是等腰三角形．
22．（10分）如图，厂房屋顶的人字架是等腰三角形，AB＝AC，AD⊥BC，若跨度BC＝16m，上弦长AB＝10m，求中柱AD的长．
【分析】由等腰三角形的性质得BC＝CD＝BC＝8（m），再由勾股定理求解即可．
【解答】解：∵AB＝AC，AD⊥BC，BC＝16m，
∴BC＝CD＝BC＝8（m），∠ADB＝90°，
∴AD＝＝＝6（m），
即中柱AD的长为6m．
23．（10分）如图，△ABC中，BC的垂直平分线DE分别交AB、BC于点D、E，且BD2﹣DA2＝AC2．
（1）求证：∠A＝90°；
（2）若AB＝8，AD：BD＝3：5，求AC的长．
【分析】（1）利用线段垂直平分线的性质可得CD＝BD，然后利用勾股定理逆定理可得结论；
（2）首先确定BD的长，进而可得CD的长，再利用勾股定理进行计算即可．
【解答】（1）证明：连接CD，
∵BC的垂直平分线DE分别交AB、BC于点D、E，
∴CD＝DB，
∵BD2﹣DA2＝AC2，
∴CD2﹣DA2＝AC2，
∴CD2＝AD2+AC2，
∴△ACD是直角三角形，且∠A＝90°；
（2）解：∵AB＝8，AD：BD＝3：5，
∴AD＝3，BD＝5，
∴DC＝5，
∴AC＝＝＝4．
24．（10分）如图，把一块等腰直角三角形零件（△ABC，其中∠ACB＝90°），放置在一凹槽内，三个顶点A，B，C分别落在凹槽内壁上，已知∠ADE＝∠BED＝90°，测得AD＝5cm，BE＝7cm，求该三角形零件的面积．
【分析】首先证明△ADC≌△CEB，根据全等三角形的性质可得DC＝BE＝7cm，再利用勾股定理计算出AC长，然后利用三角形的面积公式计算出该零件的面积即可．
【解答】解：∵△ABC是等腰直角三角形，
∴AC＝BC，∠ACB＝90°，
∴∠ACD+∠BCE＝90°，
∵∠ADC＝90°，
∴∠ACD+∠DAC＝90°，
∴∠DAC＝∠BCE，
在△ADC和△CEB中，，
∴△ADC≌△CEB（AAS），
∴DC＝BE＝7cm，
∴AC＝＝＝（cm），
∴BC＝AC＝，
∴该零件的面积为：××＝37（cm2）．
25．（12分）如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高．
（1）求证：AD垂直平分EF；
（2）若AB+AC＝10，S△ABC＝15，求DE的长．
【分析】（1）由角平分线的性质得DE＝DF，再由Rt△AED≌Rt△AFD（HL），得AE＝AF，从而证明结论；
（2）由S+＝15，代入计算即可．
【解答】（1）证明：∵AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，
∴DE＝DF，
在Rt△AED与Rt△AFD中，
，
∴Rt△AED≌Rt△AFD（HL），
∴AE＝AF，
∵DE＝DF，
∴AD垂直平分EF；
（2）解：∵DE＝DF，
∴S+＝15，
∵AB+AC＝10，
∴DE＝3．
26．（12分）如图，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝CD．
（1）证明：△BCE≌△DCF；
（2）若AB＝21，AD＝9，BC＝CD＝10，求AC的长．
【分析】（1）求出CE＝CF，∠F＝∠CEB＝90°，根据HL证出两三角形全等即可．（2）根据全等三角形对应边相等可得BE＝DF，然后求出BE的长度，然后求出AE，再根据勾股定理列式求出CE的长度，再利用勾股定理列式进行计算即可求出AC．
【解答】（1）证明：∵AC平分∠BAD，CE⊥AB，CF⊥AD，
∴CE＝CF，∠F＝∠CEB＝90°，
在Rt△BCE与Rt△DCF中，
，
∴Rt△BCE≌Rt△DCF（HL）；
（2）解：∵Rt△BCE≌Rt△DCF，
∴BE＝DF，
∵Rt△ACE≌Rt△ACF，
∴AE＝AF，
∵AB＝21，AD＝9，
∴AD+DF＝AB﹣BE，
即9+BE＝21﹣BE，
解得BE＝6，
在Rt△BCE中，CE＝＝＝8，
又∵AE＝AB﹣BE＝21﹣6＝15，
∴在Rt△ACE中，AC＝＝＝17．
27．（14分）如图，在等边△ABC中，AB＝AC＝BC＝6cm，现有两点M、N分别从点A、B同时出发，沿三角形的边运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次回到点B时，点M、N同时停止运动，设运动时间为ts．
（1）当t为何值时，M、N两点重合；
（2）当点M、N分别在AC、BA边上运动，△AMN的形状会不断发生变化．
①当t为何值时，△AMN是等边三角形；
②当t为何值时，△AMN是直角三角形；
（3）若点M、N都在BC边上运动，当存在以MN为底边的等腰△AMN时，求t的值．
【分析】（1）首先设点M、N运动x秒后，M、N两点重合，表示出M，N的运动路程，N的运动路程比M的运动路程多6cm，列出方程求解即可；
（2）①根据题意设点M、N运动t秒后，可得到等边三角形△AMN，然后表示出AM，AN的长，由于∠A等于60°，所以只要AM＝AN三角形ANM就是等边三角形；
②分别就∠AMN＝90°和∠ANM＝90°列方程求解可得；
（3）首先假设△AMN是等腰三角形，可证出△ACM≌△ABN，可得CM＝BN，设出运动时间，表示出CM，NB，NM的长，列出方程，可解出未知数的值．
【解答】解：（1）设点M、N运动x秒后，M、N两点重合，
x×1+6＝2x，
解得：x＝6，
即当M、N运动6秒时，点N追上点M；
（2）①设点M、N运动t秒后，可得到等边三角形△AMN，如图1，
AM＝t，AN＝6﹣2t，
∵∠A＝60°，当AM＝AN时，△AMN是等边三角形
∴t＝6﹣2t，
解得t＝2，
∴点M、N运动2秒后，可得到等边三角形△AMN．
②当点N在AB上运动时，如图2，
若∠AMN＝90°，∵BN＝2t，AM＝t，
∴AN＝6﹣2t，
∵∠A＝60°，
∴2AM＝AN，即2t＝6﹣2t，
解得t＝；
如图3，若∠ANM＝90°，
由2AN＝AM得2（6﹣2t）＝t，
解得t＝．
综上所述，当t为或s时，△AMN是直角三角形；
（3）当点M、N在BC边上运动时，可以得到以MN为底边的等腰三角形，
由（1）知6秒时M、N两点重合，恰好在C处，
如图4，假设△AMN是等腰三角形，
∴AN＝AM，
∴∠AMN＝∠ANM，
∴∠AMC＝∠ANB，
∵AB＝BC＝AC，
∴△ACB是等边三角形，
∴∠C＝∠B，
在△ACM和△ABN中，
∵∠AMC＝∠ANB，∠C＝∠B，AC＝AB，
∴△ACM≌△ABN（AAS），
∴CM＝BN，
∴t﹣6＝18﹣2t，
解得t＝8，符合题意．
所以假设成立，当M、N运动8秒时，能得到以MN为底的等腰三角形．