2025高考数学一轮复习-9.1-随机抽样、统计图表-专项训练【含解析】

这是一份2025高考数学一轮复习-9.1-随机抽样、统计图表-专项训练【含解析】，共10页。

C．338石D．1 365石
2．某学院A，B，C三个专业共有1 200名学生，为了调查这些学生勤工俭学的情况，拟采用分层随机抽样的方法抽取一个容量为120的样本，已知该学院的A专业有380名学生，B专业有420名学生，则应在该学院的C专业抽取的学生人数为( )
A．30B．40
C．50D．60
3．某工厂利用随机数表对生产的50个零件进行抽样测试，先将50个零件进行编号，编号分别为01,02，…，50，从中抽取5个样本，下面提供随机数表的第1行到第2行：
66 67 40 37 14 64 05 71 11 05 65 09 95 86 68
57 16 03 11 63 14 90 84 45 21 75 73 88 05 90
若从表中第1行第9列开始向右依次读取数据，则得到的第4个样本编号是( )
A．10B．09
C．71D．20
4．某市气象部门根据2021年各月的每天最高气温平均值与最低气温平均值(单位：℃)数据，绘制如下折线图：
那么，下列叙述不正确的是( )
A．各月最高气温平均值与最低气温平均值总体呈正相关
B．全年中2月份的最高气温平均值与最低气温平均值的差值最大
C．全年中各月最低气温平均值不高于10 ℃的月份有5个
D．从2021年7月至12月该市每天最高气温平均值与最低气温平均值呈下降趋势
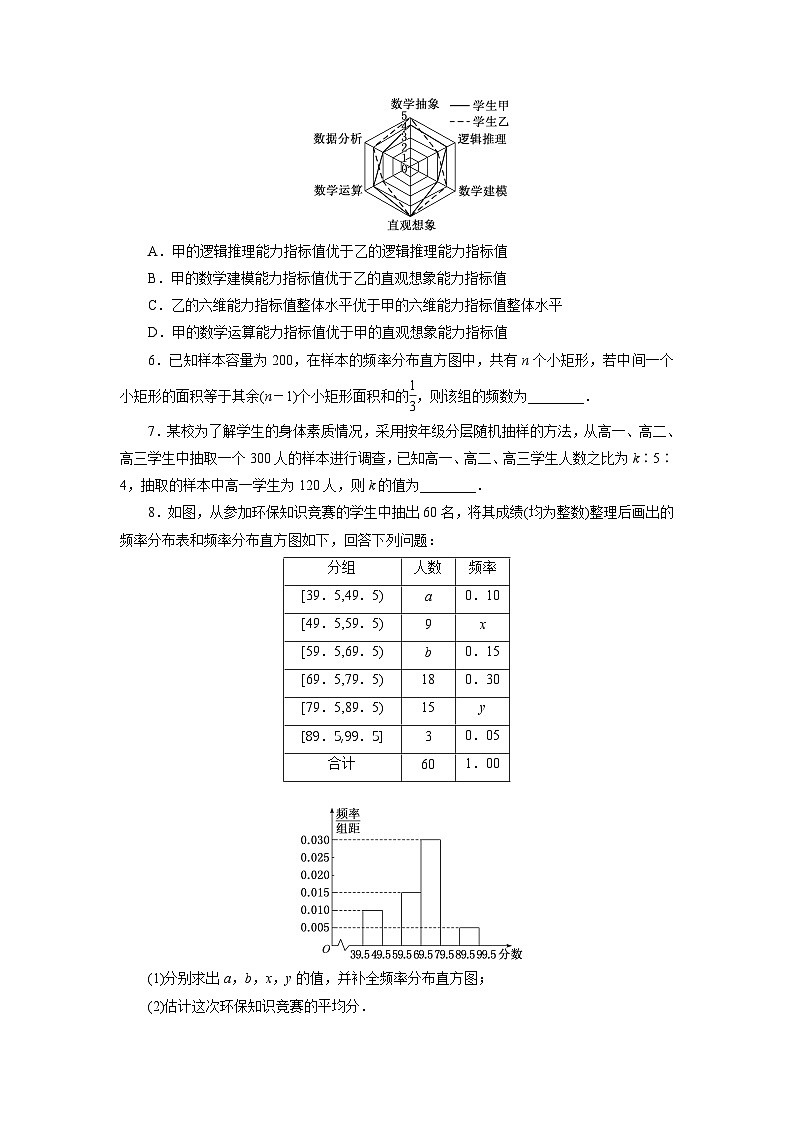
5．(多选)为了比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分，分值高者为优)，绘制了如图所示的六维能力雷达图，例如图中甲的数学抽象指标值为4，乙的数学抽象指标值为5，则下面叙述正确的是( )
A．甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B．甲的数学建模能力指标值优于乙的直观想象能力指标值
C．乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D．甲的数学运算能力指标值优于甲的直观想象能力指标值
6．已知样本容量为200，在样本的频率分布直方图中，共有n个小矩形，若中间一个小矩形的面积等于其余(n－1)个小矩形面积和的eq \f(1,3)，则该组的频数为________．
7．某校为了解学生的身体素质情况，采用按年级分层随机抽样的方法，从高一、高二、高三学生中抽取一个300人的样本进行调查，已知高一、高二、高三学生人数之比为k∶5∶4，抽取的样本中高一学生为120人，则k的值为________．
8．如图，从参加环保知识竞赛的学生中抽出60名，将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下，回答下列问题：
(1)分别求出a，b，x，y的值，并补全频率分布直方图；
(2)估计这次环保知识竞赛的平均分．
9．(多选)某地区公共部门为了调查本地区中学生的吸烟情况，对随机抽出的编号为1～1 000的1 000名学生进行了调查．调查中使用了两个问题，问题1：您的编号是否为奇数？问题2：您是否吸烟？被调查者随机从设计好的随机装置(内有除颜色外完全相同的白球100个，红球100个)中摸出一个小球：若摸出白球则回答问题1，若摸出红球则回答问题2，共有270人回答“是”，则下述正确的是( )
A．估计被调查者中约有520人吸烟
B．估计约有20人对问题2的回答为“是”
C．估计该地区约有4%的中学生吸烟
D．估计该地区约有2%的中学生吸烟
10．某工厂的三个车间在12月份共生产了3 600双皮靴，在出厂前要检查这批产品的质量，决定采用分层随机抽样的方法进行抽取，若从第一、二、三车间抽取的产品数分别为a，b，c，且a，b，c构成等差数列，则第二车间生产的产品数为________．
11．2021年7月1日是中国共产党成立100周年纪念日，某市3 000名市民参加“建党100周年”相关知识比赛，成绩统计如图所示．
(1)求a的值，并估计该市参加考试的3 000名市民中，成绩在[80,90)内的人数；
(2)若在本次比赛中前1 500名参加复赛，则进入复赛的市民的分数应当如何制定(结果用分数表示)．
12．为了解户籍性别对生育三胎选择倾向的影响，某地从育龄人群中随机抽取了容量为100的调查样本，其中城镇户籍与农村户籍各50人；男性60人，女性40人，绘制不同群体中倾向选择生育三胎与选择不生育三胎的人数比例图(如图所示)，其中阴影部分表示倾向选择生育三胎的对应比例，则下列叙述中错误的是( )
A．是否倾向选择生育三胎与户籍有关
B．是否倾向选择生育三胎与性别无关
C．倾向选择生育三胎的人员中，男性人数与女性人数相同
D．倾向选择不生育三胎的人员中，农村户籍人数少于城镇户籍人数
13．阅读下列材料，回答后面问题：
在2014年12月30日CCTV13播出的“新闻直播间”节目中，主持人说：“……假如此次亚航失联航班QZ8501被证实失事的话，2014年航空事故死亡人数将达到1 320人．尽管如此，航空安全专家还是提醒：飞机仍是相对安全的交通工具．①世界卫生组织去年公布的数据显示，每年大约有124万人死于车祸，而即使在航空事故死亡人数最多的一年，也就是1972年，其死亡数字也仅为3_346人；②截至2014年9月，每百万架次中有2．1次(指飞机失事)，乘坐汽车的百万人中其死亡人数在100人左右．”
对上述航空专家给出的①、②两段表述(划线部分)，你认为不能够支持“飞机仍是相对安全的交通工具”的所有表述序号为________．
2025高考数学一轮复习-9.1-随机抽样、统计图表-专项训练【解析版】
1．我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米1 534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为( )
A．134石 B．169石
C．338石D．1 365石
解析：B 由随机抽样的含义，该批米内夹谷约为eq \f(28,254)×1 534≈169(石)．
2．某学院A，B，C三个专业共有1 200名学生，为了调查这些学生勤工俭学的情况，拟采用分层随机抽样的方法抽取一个容量为120的样本，已知该学院的A专业有380名学生，B专业有420名学生，则应在该学院的C专业抽取的学生人数为( )
A．30B．40
C．50D．60
解析：B C专业的学生有1 200－380－420＝400(名)，由分层随机抽样知应抽取120×eq \f(400,1 200)＝40(名)．
3．某工厂利用随机数表对生产的50个零件进行抽样测试，先将50个零件进行编号，编号分别为01,02，…，50，从中抽取5个样本，下面提供随机数表的第1行到第2行：
66 67 40 37 14 64 05 71 11 05 65 09 95 86 68
57 16 03 11 63 14 90 84 45 21 75 73 88 05 90
若从表中第1行第9列开始向右依次读取数据，则得到的第4个样本编号是( )
A．10B．09
C．71D．20
解析：B 从随机数表第1行的第9列数字开始由左向右每次连续读取2个数字，删除超出范围及重复的编号，符合条件的编号有14,05,11,09，所以选出来的第4个个体的编号为09，故选B．
4．某市气象部门根据2021年各月的每天最高气温平均值与最低气温平均值(单位：℃)数据，绘制如下折线图：
那么，下列叙述不正确的是( )
A．各月最高气温平均值与最低气温平均值总体呈正相关
B．全年中2月份的最高气温平均值与最低气温平均值的差值最大
C．全年中各月最低气温平均值不高于10 ℃的月份有5个
D．从2021年7月至12月该市每天最高气温平均值与最低气温平均值呈下降趋势
解析：D 对于A项，根据折线图可以发现除2月份外，各月最低气温平均值越高，最高气温平均值也越高，总体呈正相关，A项正确；对于B项，通过折线图观察，2月份的两个点距离最大，B项正确；对于C项，各月最低气温平均值不高于10 ℃的有1月，2月，3月，11月，12月，共有5个月，C项正确；对于D项，观察折线图可知，7月份到8月份气温在上升，D项错误．
5．(多选)为了比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分，分值高者为优)，绘制了如图所示的六维能力雷达图，例如图中甲的数学抽象指标值为4，乙的数学抽象指标值为5，则下面叙述正确的是( )
A．甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B．甲的数学建模能力指标值优于乙的直观想象能力指标值
C．乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D．甲的数学运算能力指标值优于甲的直观想象能力指标值
解析：AC 对于选项A，甲的逻辑推理能力指标值为4，优于乙的逻辑推理能力指标值为3，故A正确；对于选项B，甲的数学建模能力指标值为3，乙的直观想象能力指标值为5，所以乙的直观想象能力指标值优于甲的数学建模能力指标值，故B错误；对于选项C，甲的六维能力指标值的平均值为eq \f(1,6)×(4＋3＋4＋5＋3＋4)＝eq \f(23,6)，乙的六维能力指标值的平均值为eq \f(1,6)×(5＋4＋3＋5＋4＋3)＝4，eq \f(23,6)＜4，故C正确；对于选项D，甲的数学运算能力指标值为4，甲的直观想象能力指标值为5，所以甲的数学运算能力指标值不优于甲的直观想象能力指标值，故D错误．故选A、C．
6．已知样本容量为200，在样本的频率分布直方图中，共有n个小矩形，若中间一个小矩形的面积等于其余(n－1)个小矩形面积和的eq \f(1,3)，则该组的频数为________．
解析：设除中间一个小矩形外的(n－1)个小矩形面积的和为p，则中间一个小矩形面积为eq \f(1,3)p，p＋eq \f(1,3)p＝1，p＝eq \f(3,4)，则中间一个小矩形的面积等于eq \f(1,3)p＝eq \f(1,4)，200×eq \f(1,4)＝50，即该组的频数为50．
答案：50
7．某校为了解学生的身体素质情况，采用按年级分层随机抽样的方法，从高一、高二、高三学生中抽取一个300人的样本进行调查，已知高一、高二、高三学生人数之比为k∶5∶4，抽取的样本中高一学生为120人，则k的值为________．
解析：由题意可知，eq \f(120,300)＝eq \f(k,k＋5＋4)，解得k＝6．
答案：6
8．如图，从参加环保知识竞赛的学生中抽出60名，将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下，回答下列问题：
(1)分别求出a，b，x，y的值，并补全频率分布直方图；
(2)估计这次环保知识竞赛的平均分．
解：(1)a＝6，b＝9，x＝0．15，y＝0．25，
补全频率分布直方图如图，
(2)用各组中值估计平均分为44．5×0．1＋54．5×0．15＋64．5×0．15＋74．5×0．3＋84．5×0．25＋94．5×0．05＝70．5．
故这次环保知识竞赛的平均分约为70．5．
9．(多选)某地区公共部门为了调查本地区中学生的吸烟情况，对随机抽出的编号为1～1 000的1 000名学生进行了调查．调查中使用了两个问题，问题1：您的编号是否为奇数？问题2：您是否吸烟？被调查者随机从设计好的随机装置(内有除颜色外完全相同的白球100个，红球100个)中摸出一个小球：若摸出白球则回答问题1，若摸出红球则回答问题2，共有270人回答“是”，则下述正确的是( )
A．估计被调查者中约有520人吸烟
B．估计约有20人对问题2的回答为“是”
C．估计该地区约有4%的中学生吸烟
D．估计该地区约有2%的中学生吸烟
解析：BC 随机抽出的1 000名学生中，回答第一个问题的概率是eq \f(1,2)， 其编号是奇数的概率也是eq \f(1,2)， 所以回答问题1且回答是的人数大约为1 000×eq \f(1,2)×eq \f(1,2)＝250，所以回答第二个问题，且为是的人数大约为270－250＝20, 由此估计此地区中学生吸烟人数的百分比为eq \f(20,500)＝4%，估计被调查者中约有1 000×4%＝40(人)吸烟，故表述正确的是B、C． 故选B、C．
10．某工厂的三个车间在12月份共生产了3 600双皮靴，在出厂前要检查这批产品的质量，决定采用分层随机抽样的方法进行抽取，若从第一、二、三车间抽取的产品数分别为a，b，c，且a，b，c构成等差数列，则第二车间生产的产品数为________．
解析：因为a，b，c成等差数列，所以2b＝a＋c．所以eq \f(b,a＋b＋c)＝eq \f(1,3)．所以第二车间抽取的产品数占抽样产品总数的eq \f(1,3)．根据分层随机抽样的性质，可知第二车间生产的产品数占总数的eq \f(1,3)，即为eq \f(1,3)×3 600＝1 200．
答案：1 200
11．2021年7月1日是中国共产党成立100周年纪念日，某市3 000名市民参加“建党100周年”相关知识比赛，成绩统计如图所示．
(1)求a的值，并估计该市参加考试的3 000名市民中，成绩在[80,90)内的人数；
(2)若在本次比赛中前1 500名参加复赛，则进入复赛的市民的分数应当如何制定(结果用分数表示)．
解：(1)依题意，(2a＋3a＋7a＋6a＋2a)×10＝1，
解得a＝0．005．
故成绩在[80,90)内的频率为0．3，
故所求人数为3 000×0．3＝900．
(2)依题意，要前1 500名市民参加复赛，即求该组数据的中位数，
所以分数为70＋(0．5－0．1－0．15)÷0．035＝77eq \f(1,7)．
12．为了解户籍性别对生育三胎选择倾向的影响，某地从育龄人群中随机抽取了容量为100的调查样本，其中城镇户籍与农村户籍各50人；男性60人，女性40人，绘制不同群体中倾向选择生育三胎与选择不生育三胎的人数比例图(如图所示)，其中阴影部分表示倾向选择生育三胎的对应比例，则下列叙述中错误的是( )
A．是否倾向选择生育三胎与户籍有关
B．是否倾向选择生育三胎与性别无关
C．倾向选择生育三胎的人员中，男性人数与女性人数相同
D．倾向选择不生育三胎的人员中，农村户籍人数少于城镇户籍人数
解析：C 由不同群体中倾向选择生育三胎与倾向选择不生育三胎的人数比例图知：在A中，城镇户籍倾向选择生育三胎的比例为40%，农村户籍倾向选择生育三胎的比例为80%，∴是否倾向选择生育三胎与户籍有关，故A正确；在B中，男性倾向选择生育三胎的比例为60%，女性倾向选择生育三胎的比例为60%，∴是否倾向选择生育三胎与性别无关，故B正确；在C中，男性倾向选择生育三胎的比例为60%，人数为60×60%＝36人，女性倾向选择生育三胎的比例为60%，人数为40×60%＝24人，∴倾向选择生育三胎的人员中，男性人数比女性人数多，故C错误；在D中，倾向选择不生育三胎的人员中，农村户籍人数为50×(1－80%)＝10人，城镇户籍人数为50×(1－40%)＝30人，∴倾向选择不生育三胎的人员中，农村户籍人数少于城镇户籍人数，故D正确．故选C．
13．阅读下列材料，回答后面问题：
在2014年12月30日CCTV13播出的“新闻直播间”节目中，主持人说：“……假如此次亚航失联航班QZ8501被证实失事的话，2014年航空事故死亡人数将达到1 320人．尽管如此，航空安全专家还是提醒：飞机仍是相对安全的交通工具．①世界卫生组织去年公布的数据显示，每年大约有124万人死于车祸，而即使在航空事故死亡人数最多的一年，也就是1972年，其死亡数字也仅为3_346人；②截至2014年9月，每百万架次中有2．1次(指飞机失事)，乘坐汽车的百万人中其死亡人数在100人左右．”
对上述航空专家给出的①、②两段表述(划线部分)，你认为不能够支持“飞机仍是相对安全的交通工具”的所有表述序号为________．
解析：表述①虽是同类数据，但反映不出乘车出行和乘飞机出行的总人数的关系；
表述②两个数据不是同一类数据，这与每架次飞机的乘机人数有关；但是可以做如下大致估算，考虑平均每架次飞机的乘机人数为x，这样每百万人乘机死亡人数2．1人，要远远少于乘车每百万人中死亡人数．
答案：①
分组
人数
频率
[39．5,49．5)
a
0．10
[49．5,59．5)
9
x
[59．5,69．5)
b
0．15
[69．5,79．5)
18
0．30
[79．5,89．5)
15
y
[89．5,99．5]
3
0．05
合计
60
1．00
分组
人数
频率
[39．5,49．5)
a
0．10
[49．5,59．5)
9
x
[59．5,69．5)
b
0．15
[69．5,79．5)
18
0．30
[79．5,89．5)
15
y
[89．5,99．5]
3
0．05
合计
60
1．00