2025高考数学一轮复习-9.3-成对数据的统计分析-专项训练【含解析】

这是一份2025高考数学一轮复习-9.3-成对数据的统计分析-专项训练【含解析】，共10页。

A. 变量x 与y 负相关，x 与z 正相关B. 变量x 与y 负相关，x 与z 负相关
C. 变量x 与y 正相关，x 与z 正相关D. 变量x 与y 正相关，x 与z 负相关
2. [2023·山东德州模拟]已知两个变量具有线性相关性，现通过最小二乘法求经验回归方程y=bx+a ，将已知数据代入公式Q=∑ni=1yi−bxi−a2 计算后得到的代数式为3a2+13b2+12ab−2b+3 ，使上述代数式取值最小的a ，b 的值即为经验回归方程的系数，则经验回归方程为( )
A. y=−x+2 B. y=−x−2 C. y=x+2 D. y=x−2
3. 为了弘扬中国茶文化，某酒店推出特色茶食品“排骨茶”，为了解每壶“排骨茶”中所放茶叶量x （单位：克）与食客的满意率y 的关系，通过调查研究发现可选择函数模型y=1100ekx+c 来拟合y 与x 的关系，根据以下数据：
可求得y 关于x 的回归方程为( )
A. y=1100e0.043x+4.291 B. y=1100e0.043x−4.291
C. y=e0.043x+4.291 D. y=e0.043x−4.291
4. [2023·江苏南京模拟]高二某班数学学习小组成员最近研究的椭圆的问题数x 与抛物线的问题数y 之间有如下的对应数据：
若用最小二乘法求得经验回归方程是y=710x+1910 ，则表中的m 的值是 .
5. [2023·安徽合肥检测]某公司一种型号的产品近期销售情况如下表：
根据上表可得到经验回归方程y=0.75x+a ,据此估计，该公司7月份这种型号产品的销售额为 万元.
6. [2023·山东泰安模拟]某班统计了本班同学1~7月份的人均月劳动时间（单位：时），并建立了人均月劳动时间y 关于月份x 的经验回归方程y=bx+4 ，y 与x 的原始数据如表所示：
由于某些原因导致部分数据丢失，但已知∑7i=1xiyi=452 .
（1） 求m ，n 的值；
（2） 求该班6月份人均月劳动时间数据的残差值.（残差即样本数据与预测值之差）
参考公式：在经验回归方程y=bx+a 中，b=∑ni=1xiyi−nxy∑ni=1xi2−nx2,a=y−bx ，a=y−bx .
[B级 综合运用]
7. [2022·高考全国卷乙]某地经过多年的环境治理，已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位：m2 ）和材积量（单位：m3 ），得到如下数据：
并计算得∑10i=1xi2=0.038 ,∑10i=1yi2=1.6158 ,∑10i=1xiyi=0.2474 .
（1） 估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；
（2） 求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到0.01）；
（3） 现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为186m2 .已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
附：相关系数r=∑ni=1xi−xyi−y∑ni=1xi−x2∑ni=1yi−y2 ,1.896≈1.377 .
8. 中国茶文化博大精深，已知茶水的口感与茶叶类型以及水温有关.经验表明，某种绿茶用85℃ 的水泡制，再等到茶水温度降至60℃ 时饮用，可以产生最佳口感.某学习研究小组通过测量，得到了下面表格的数据（室温是20℃ ）.
（1） 小组成员根据上面表格中的数据绘制散点图，并根据散点图分布情况，考虑到茶水温度降到室温（即20℃ ）就不能再降的事实，决定选择函数模型y=kcx+20x≥0 来刻画.
① 令z=lny−20 ,求出z 关于x 的经验回归方程；
② 利用①的结论，求出y=kcx+20x≥0,c>0 中的k 与c .
（2） 你认为该品种绿茶用85℃ 的水大约泡制多久后饮用，可以产生最佳口感？
参考数据：ln65≈4.2 ,ln59≈4.1 ,ln54≈4.0 ,ln51≈3.9 ,ln45≈3.8 ,lg0.90.6≈4.8 ,e−0.1≈0.9 ,e4.2≈66.7 ,400667≈0.6 .参考公式：z=bx+a ,∑ni=1xi−xzi−z∑ni=1xi−x2,a=z−bx ,a=z−bx .
2025高考数学一轮复习-9.3-成对数据的统计分析-专项训练【解析版】
[A级 基础达标]
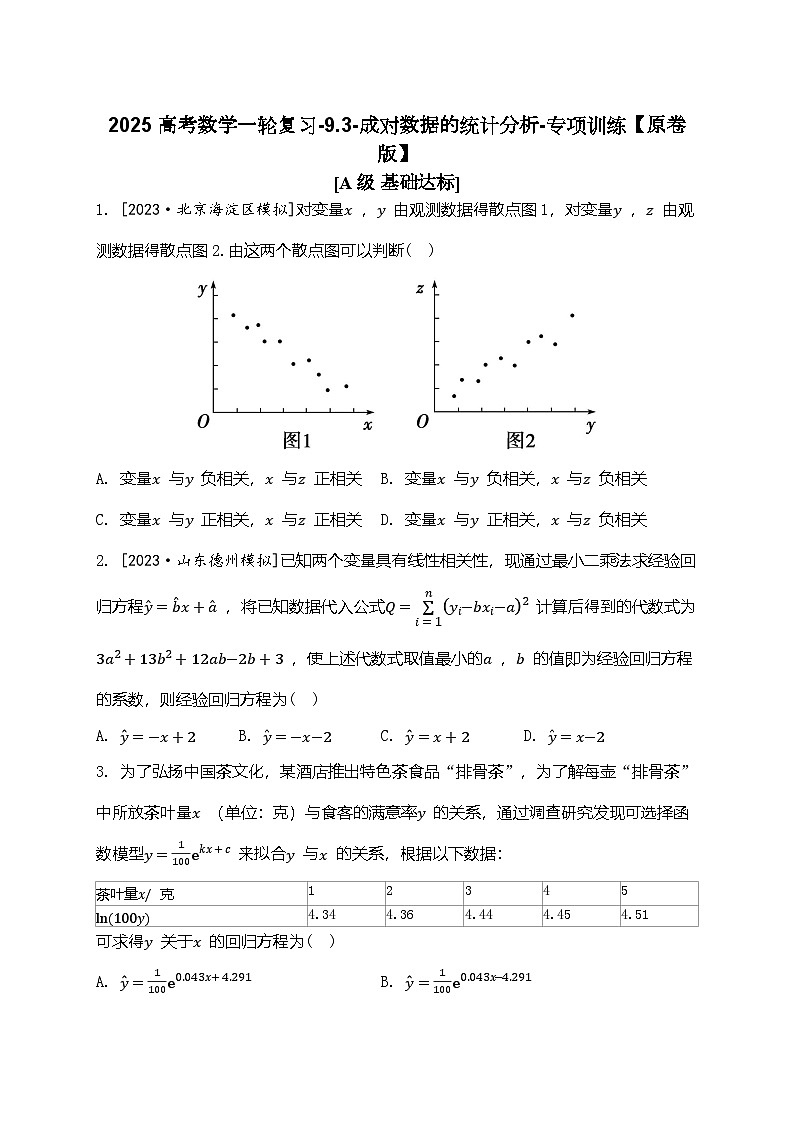
1. [2023·北京海淀区模拟]对变量x ，y 由观测数据得散点图1，对变量y ，z 由观测数据得散点图2.由这两个散点图可以判断( B )
A. 变量x 与y 负相关，x 与z 正相关B. 变量x 与y 负相关，x 与z 负相关
C. 变量x 与y 正相关，x 与z 正相关D. 变量x 与y 正相关，x 与z 负相关
[解析]选B.由散点图可知，变量x 与y 负相关，变量y 与z 正相关，所以x 与z 负相关.故选B.
2. [2023·山东德州模拟]已知两个变量具有线性相关性，现通过最小二乘法求经验回归方程y=bx+a ，将已知数据代入公式Q=∑ni=1yi−bxi−a2 计算后得到的代数式为3a2+13b2+12ab−2b+3 ，使上述代数式取值最小的a ，b 的值即为经验回归方程的系数，则经验回归方程为( D )
A. y=−x+2 B. y=−x−2 C. y=x+2 D. y=x−2
[解析]选D.3a2+13b2+12ab−2b+3=3a+2b2+b−12+2 ,
当a+2b=0，b−1=0， 即a=−2，b=1 时上式最小，故y=x−2 .故选D.
3. 为了弘扬中国茶文化，某酒店推出特色茶食品“排骨茶”，为了解每壶“排骨茶”中所放茶叶量x （单位：克）与食客的满意率y 的关系，通过调查研究发现可选择函数模型y=1100ekx+c 来拟合y 与x 的关系，根据以下数据：
可求得y 关于x 的回归方程为( A )
A. y=1100e0.043x+4.291 B. y=1100e0.043x−4.291
C. y=e0.043x+4.291 D. y=e0.043x−4.291
[解析]选A.由表中数据可知x=1+2+3+4+55=3 ，15×4.34+4.36+4.44+4.45+4.51=4.42 .
对于A，y=1100e0.043x+4.291 化简变形可得100y=e0.043x+4.291 ，两边同时取对数可得ln100y=0.043x+4.291 ，将x=3 代入可得ln100y=0.043×3+4.291=4.42 ，与题中数据吻合，故选项A正确；
对于B，y=1100e0.043x−4.291 化简变形可得100y=e0.043x−4.291 ，两边同时取对数可得ln100y=0.043x−4.291 ，将x=3 代入可得ln100y=0.043×3−4.291=−4.162≠4.42 ，所以选项B错误；
对于C，y=e0.043x+4.291 ，两边同时取对数可得lny=0.043x+4.291 ，而表中所给数据为ln100y 的相关量，所以C错误；同理可知D错误.故选A.
4. [2023·江苏南京模拟]高二某班数学学习小组成员最近研究的椭圆的问题数x 与抛物线的问题数y 之间有如下的对应数据：
若用最小二乘法求得经验回归方程是y=710x+1910 ，则表中的m 的值是4.
[解析]由题意得x=15×1+2+3+4+5=3 ，y=15×2+m+4+5+5=16+m5 ，因为经验回归直线恒过样本中心点x,y ，
所以16+m5=710×3+1910 ，解得m=4 .
5. [2023·安徽合肥检测]某公司一种型号的产品近期销售情况如下表：
根据上表可得到经验回归方程y=0.75x+a ,据此估计，该公司7月份这种型号产品的销售额为19.05万元.
[解析]由题意,x=2+3+4+5+65=4 ,
y=15.1+16.3+17.0+17.2+18.45=16.8 ,
经验回归直线y=0.75x+a 过点x,y ,
可得a=13.8 ,当x=7 时，可得y=0.75×7+13.8=19.05 .
6. [2023·山东泰安模拟]某班统计了本班同学1~7月份的人均月劳动时间（单位：时），并建立了人均月劳动时间y 关于月份x 的经验回归方程y=bx+4 ，y 与x 的原始数据如表所示：
由于某些原因导致部分数据丢失，但已知∑7i=1xiyi=452 .
（1） 求m ，n 的值；
[答案]解：由表知，x=17×1+2+3+4+5+6+7=4 ，
y =17×8+9+m+12+n+19+22=70+m+n7 ，
所以∑7i=1xi2−7x2=12+22+32+42+52+62+72−7×42=28 ，
所以b=∑7i=1xiyi−7xy∑7i=1xi2−7x2=452−7×4×70+m+n728 ，即m+n=43−7b ，①
因为经验回归直线恒过样本中心点x,y ，
所以70+m+n7=4b+4 ，即m+n=28b−42 ，②
由①②，得b=177 ,m+n=26 ,③
因为∑7i=1xiyi=8+18+3m+48+5n+114+154=452 ,所以3m+5n=110 ，④
由③④，得m=10 ，n=16 .
（2） 求该班6月份人均月劳动时间数据的残差值.（残差即样本数据与预测值之差）
参考公式：在经验回归方程y=bx+a 中，b=∑ni=1xiyi−nxy∑ni=1xi2−nx2,a=y−bx ，a=y−bx .
[答案]由（1）知，经验回归方程为y=177x+4 ，
所以当x=6 时，预测值y=177×6+4=1307 ，此时残差为19−1307=37 .
[B级 综合运用]
7. [2022·高考全国卷乙]某地经过多年的环境治理，已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位：m2 ）和材积量（单位：m3 ），得到如下数据：
并计算得∑10i=1xi2=0.038 ,∑10i=1yi2=1.6158 ,∑10i=1xiyi=0.2474 .
（1） 估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；
[答案]解：估计该林区这种树木平均一棵的根部横截面积
x=∑10i=1xi10=0.610=0.06 ,
估计该林区这种树木平均一棵的材积量
y=∑10i=1yi10=3.910=0.39 .
（2） 求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到0.01）；
[答案]∑10i=1xi−xyi−y=∑10i=1xiyi−10xy=0.0134 ,
∑10i=1xi−x2=∑10i=1xi2−10x2=0.002 ,
∑10i=1yi−y2=∑10i=1yi2−10y2=0.0948 ,
所以∑10i=1xi−x2∑10i=1yi−y2=0.002×0.0948=0.0001×1.896≈0.01×1.377=0.01377 ,
所以样本相关系数r=∑10i=1xi−xyi−y∑10i=1xi−x2∑10i=1yi−y2≈≈0.97 .
（3） 现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为186m2 .已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
附：相关系数r=∑ni=1xi−xyi−y∑ni=1xi−x2∑ni=1yi−y2 ,1.896≈1.377 .
[答案]设该林区这种树木的总材积量的估计值为Ym3 ,由题意可知，该种树木的材积量与其根部横截面积近似成正比，所以 ,
所以Y=186× ，即该林区这种树木的总材积量的估计值为1209m3 .
8. 中国茶文化博大精深，已知茶水的口感与茶叶类型以及水温有关.经验表明，某种绿茶用85℃ 的水泡制，再等到茶水温度降至60℃ 时饮用，可以产生最佳口感.某学习研究小组通过测量，得到了下面表格的数据（室温是20℃ ）.
（1） 小组成员根据上面表格中的数据绘制散点图，并根据散点图分布情况，考虑到茶水温度降到室温（即20℃ ）就不能再降的事实，决定选择函数模型y=kcx+20x≥0 来刻画.
① 令z=lny−20 ,求出z 关于x 的经验回归方程；
[答案]解：由已知得出x 与z 的关系，如下表：
设经验回归方程为z=bx+a ,
由题意，得x=0+1+2+3+45=2 ,
z=4.2+4.1+4.0+3.9+3.85=4 ，
所以∑5i=1xi−xzi−z=−2×0.2+−1×0.1+1×−0.1+2×−0.2=−1 ,
∑5i=1xi−x2=−22+−12+12+22=10 ，
则b=∑5i=1xi−xzi−z∑5i=1xi−x2=−110=−0.1 ,
a=z−bx=4+0.1×2=4.2 ,
则z 关于x 的经验回归方程为z=−0.1x+4.2 .
② 利用①的结论，求出y=kcx+20x≥0,c>0 中的k 与c .
[答案]由y=kcx+20x≥0 ,得y−20=kcxx≥0 ,
两边取对数得，lny−20=lnk+xlnc ,
利用①的结论得lnc=−0.1 ,lnk=4.2 ,
所以c=e−0.1≈0.9 ,k=e4.2≈66.7 .
（2） 你认为该品种绿茶用85℃ 的水大约泡制多久后饮用，可以产生最佳口感？
参考数据：ln65≈4.2 ,ln59≈4.1 ,ln54≈4.0 ,ln51≈3.9 ,ln45≈3.8 ,lg0.90.6≈4.8 ,e−0.1≈0.9 ,e4.2≈66.7 ,400667≈0.6 .参考公式：z=bx+a ,∑ni=1xi−xzi−z∑ni=1xi−x2,a=z−bx ,a=z−bx .
[答案]由（1）得，y=66.7×0.9x+20x≥0 ,
令y=60 ,得x≈lg0.90.6≈4.8 .
所以该品种绿茶用85℃ 的水大约泡制4.8min 后饮用口感最佳.
茶叶量x/ 克
1
2
3
4
5
ln100y
4.34
4.36
4.44
4.45
4.51
x
1
2
3
4
5
y
2
m
4
5
5
月份x
2
3
4
5
6
销售额y/ 万元
15.1
16.3
17.0
17.2
18.4
月份x
1
2
3
4
5
6
7
人均月劳动时间y
8
9
m
12
n
19
22
样本号i
1
2
3
4
5
6
7
8
9
10
总和
根部横截面积xi
0.04
0.06
0.04
0.08
0.08
0.05
0.05
0.07
0.07
0.06
0.6
材积量yi
0.25
0.40
0.22
0.54
0.51
0.34
0.36
0.46
0.42
0.40
3.9
泡制时间x/min
0
1
2
3
4
水温y/℃
85
79
74
71
65
茶叶量x/ 克
1
2
3
4
5
ln100y
4.34
4.36
4.44
4.45
4.51
x
1
2
3
4
5
y
2
m
4
5
5
月份x
2
3
4
5
6
销售额y/ 万元
15.1
16.3
17.0
17.2
18.4
月份x
1
2
3
4
5
6
7
人均月劳动时间y
8
9
m
12
n
19
22
样本号i
1
2
3
4
5
6
7
8
9
10
总和
根部横截面积xi
0.04
0.06
0.04
0.08
0.08
0.05
0.05
0.07
0.07
0.06
0.6
材积量yi
0.25
0.40
0.22
0.54
0.51
0.34
0.36
0.46
0.42
0.40
3.9
泡制时间x/min
0
1
2
3
4
水温y/℃
85
79
74
71
65
泡制时间x/min
0
1
2
3
4
z
4.2
4.1
4.0
3.9
3.8