2025年高考数学一轮复习4.3.2-简单的三角恒等变换-专项训练【含解析】

这是一份2025年高考数学一轮复习4.3.2-简单的三角恒等变换-专项训练【含解析】，共7页。试卷主要包含了单项选择题，多项选择题，填空题等内容，欢迎下载使用。
1.cs2π12-cs25π12=( )
A.12B.33C.22D.32
2已知sinα+π4=-32,则sin 2α的值为( )
A.12B.-12
C.32D.-32
3.某学生在“捡起树叶树枝,净化校园环境”的志愿活动中拾到了三支小树枝(视为三条线段),想要用它们作为三角形的三条高线制作一个三角形.经测量,其长度分别为3 cm,4 cm,6 cm,则( )
A.能作出两个锐角三角形
B.能作出一个直角三角形
C.能作出一个钝角三角形
D.不能作出这样的三角形
4.设sin 20°=m,cs 20°=n,化简1+tan10°1-tan10°−2cs70°cs50°=( )
A.nmB.-mn
C.mnD.-nm
5.在△ABC中,AC=22,BC=4,则角B的最大值为( )
A.π4B.π3
C.π2D.π6
6.设M,N为某海边相邻的两座山峰,到海平面的距离分别为100米,50米.现欲在M,N之间架设高压电网,须计算M,N之间的距离.勘测人员在海平面上选取一点P,利用测角仪从P点测得的M,N点的仰角分别为30°,45°,并从P点观测到M,N点的视角为45°,则M,N之间的距离为( )
A.5010米
B.5014米
C.5022米
D.5026米
7.若sin 2α=55,sin(β-α)=1010,且α∈π4,π2,β∈π,3π2,则α+β的值是( )
A.7π4B.9π4
C.5π4或7π4D.7π4或9π4
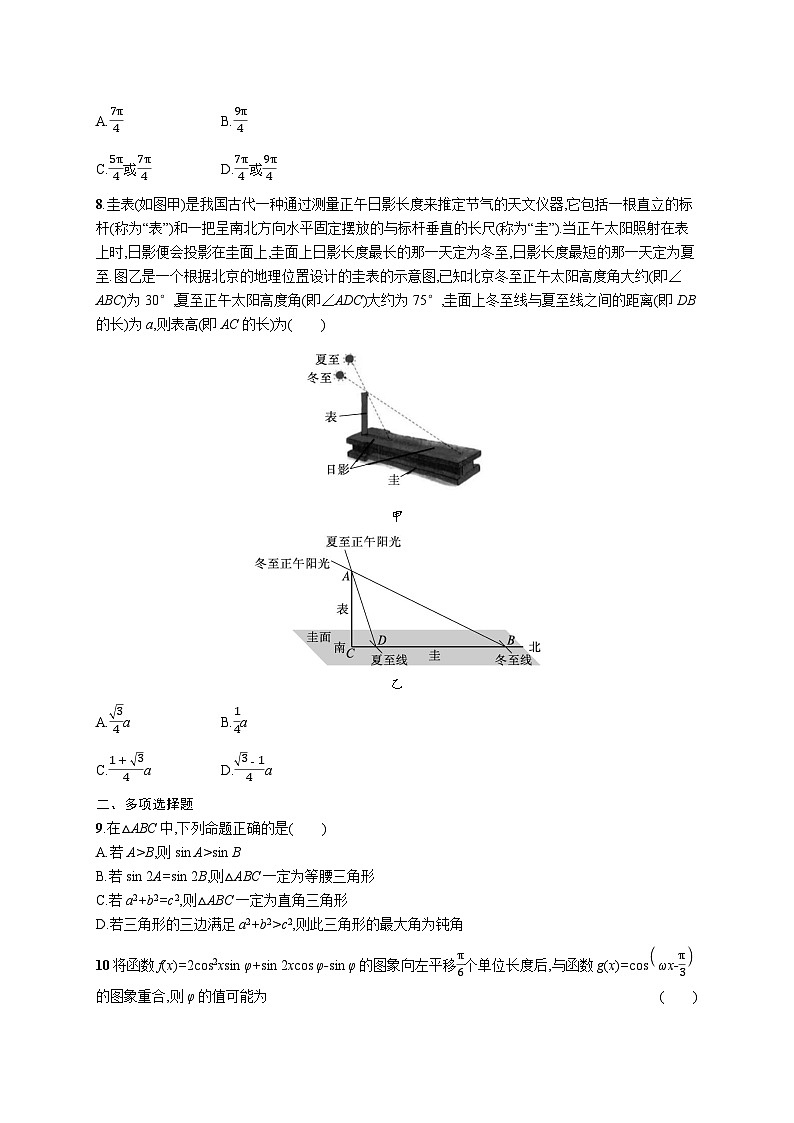
8.圭表(如图甲)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆(称为“表”)和一把呈南北方向水平固定摆放的与标杆垂直的长尺(称为“圭”).当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图乙是一个根据北京的地理位置设计的圭表的示意图,已知北京冬至正午太阳高度角大约(即∠ABC)为30°,夏至正午太阳高度角(即∠ADC)大约为75°,圭面上冬至线与夏至线之间的距离(即DB的长)为a,则表高(即AC的长)为( )
甲
乙
A.34aB.14a
C.1+34aD.3-14a
二、多项选择题
9.在△ABC中,下列命题正确的是( )
A.若A>B,则sin A>sin B
B.若sin 2A=sin 2B,则△ABC一定为等腰三角形
C.若a2+b2=c2,则△ABC一定为直角三角形
D.若三角形的三边满足a2+b2>c2,则此三角形的最大角为钝角
10将函数f(x)=2cs2xsin φ+sin 2xcs φ-sin φ的图象向左平移π6个单位长度后,与函数g(x)=csωx-π3的图象重合,则φ的值可能为( )
A.-3π2B.-π3
C.-π6D.2π3
11.我国古代著名的数学家赵爽在《周髀算经》中利用一副“弦图”,根据面积关系给出了勾股定理的证明,后人称其为“赵爽弦图”.如图1,它由四个全等的直角三角形与一个小正方形拼成的一个大正方形.我们通过类比得到图2,它是由三个全等的钝角三角形与一个小等边三角形A'B'C'拼成的一个大等边三角形ABC.对于图2,下列结论正确的是( )
图1
图2
A.这三个全等的钝角三角形不可能是等腰三角形
B.若BB'=3,sin∠ABB'=5314,则A'B'=2
C.若AB=2A'B',则AB'=5BB'
D.若A'是AB'的中点,则三角形ABC的面积是三角形A'B'C'面积的7倍
三、填空题
12.若tan(α-β)=32,tan β=2,则tan α= .
13.若函数f(x)=sin(x+φ)+cs x的最大值为2,则常数φ的一个取值为 .
14.设锐角△ABC的内角A,B,C的对边分别为a,b,c,若B=2A,则b+ca的取值范围是 .
15.已知定义在x∈-3π4,π4上的函数f(x)=sinx+π4+sin 2x在x=θ处取得最小值,则最小值为 ,此时cs θ= .
参考答案与解析
1.D 解析 原式=cs2π12-cs2π2−π12=cs2π12-sin2π12=csπ6=32.
2.A 解析 因为sinα+π4=-32,所以sin 2α=-cs2α+π2=-cs 2α+π4=2sin2α+π4-1=2-322-1=12.
3.C 解析 因为三条高线的长度为3 cm,4 cm,6 cm,故三边之比为4∶3∶2,
设最大边所对的角为α,则cs α=4+9-162×2×3=-140,由余弦定理可得cs B=AB2+BC2-AC22AB·BC=x2+88x=x8+1x≥2x8·1x=22,
当且仅当x=22时,等号成立,因为0sin B,A正确;对于选项B,若sin 2A=sin 2B,则2A=2B或2A+2B=π,即A=B或A+B=π2,所以△ABC为等腰三角形或直角三角形,B错误;对于选项C,若a2+b2=c2,由勾股定理的逆定理可知△ABC一定为直角三角形,C正确;对于选项D,若三角形的三边满足a2+b2>c2,由余弦定理可知cs C>0,仅可得C为锐角,最大角是否为钝角不确定,D错误.
10.AC 解析 f(x)=(1+cs 2x)sin φ+sin 2xcs φ-sin φ=cs 2xsin φ+sin 2xcs φ=sin(2x+φ),将f(x)的图象向左平移π6个单位长度得y=sin2x+π6+φ=sin2x+π3+φ的图象,与函数g(x)=csωx-π3的图象重合,故ω=±2,
①若g(x)=cs2x-π3=sin2x-π3+π2=sin2x+π6,π3+φ=π6+2kπ,φ=2kπ-π6(k∈Z),结合选项,φ=-π6符合.
②若g(x)=cs-2x-π3=cs2x+π3=sin2x+π3+π2=sin2x+5π6,π3+φ=5π6+2kπ,φ=2kπ+π2(k∈Z),结合选项,φ=-3π2符合.
11.ABD 解析 对于A选项,根据题意,图2是由三个全等的钝角三角形与一个小等边三角形A'B'C'拼成的一个大等边三角形ABC,故AA'=BB',AB'>BB',所以这三个全等的钝角三角形不可能是等腰三角形,故A选项正确;
对于B选项,由题知,在△ABB'中,BB'=3,sin∠ABB'=5314,∠AB'B=120°,所以sin∠BAB'=sin(60°-∠ABB')=3314,所以由正弦定理得BB'sin∠BAB'=AB'sin∠ABB',解得AB'=5,因为BB'=AA'=3,所以A'B'=2,故B选项正确;
对于C选项,不妨设AB=2A'B'=2,AA'=x,所以在△AB'B中,由余弦定理得|AB|2=|AB'|2+|BB'|2-2|AB'||BB'|cs∠AB'B,代入数据得AA'=x=5-12,所以AB'=AA'+A'B'=1+5-12=5+12,BB'=AA'=5-12,所以AB'BB'=5+15-1,故C选项错误;
对于D选项,若A'是AB'的中点,则S△ABB'=12BB'·AB'sin 120°=B'C'·A'B'sin 60°=2S△A'B'C',所以S△ABC=3S△ABB'+S△A'B'C'=7S△A'B'C',故D选项正确.
12.-74 解析 因为tan(α-β)=32,tan β=2,所以tan α=tan[(α-β)+β]=tan(α-β)+tanβ1-tan(α-β)·tanβ=32+21-32×2=-74.
13.π2答案不唯一,φ=2kπ+π2,k∈Z均可 解析 因为f(x)=cs φsin x+(sin φ+1)cs x=cs 2φ+(sinφ+1)2sin(x+θ),所以cs 2φ+(sinφ+1)2=2,解得sin φ=1,故可取φ=π2.
14.(2+1,3+2) 解析 因为B=2A,则sin B=sin 2A=2sin Acs A,cs B=cs 2A=2cs2A-1,
又sin C=sin(A+B)=sin Acs B+cs Asin B,
故由正弦定理可得b+ca=sinB+sinCsinA=2cs A+cs B+csAsinBsinA=2cs A+cs B+2cs2A=2cs A+2cs2A+2cs2A-1=4cs2A+2cs A-1.
又△ABC为锐角三角形,故可得A∈0,π2,B=2A∈0,π2,C=π-3A∈0,π2,解得A∈π6,π4,则cs A∈22,32,故4cs2A+2cs A-1∈(2+1,3+2),即b+ca∈(2+1,3+2).
15.-98 30-28 解析 因为x∈-3π4,π4,则x+π4∈-π2,π2,令t=sinx+π4∈[-1,1],则t=22(sin x+cs x),t2=12(1+2sin xcs x)=12(1+sin 2x),则sin 2x=2t2-1,所以f(x)=t+2t2-1=2t2+t-1,所以当t=-14时,函数y=2t2+t-1取得最小值,即ymin=18−14-1=-98,此时sinθ+π4=-14,
由已知θ+π4∈-π2,π2,
所以csθ+π4=1-sin2θ+π4=154,cs θ=csθ+π4-π4=csθ+π4csπ4+sinθ+π4sinπ4=30-28.