2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练【含答案】

这是一份2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练【含答案】，共12页。试卷主要包含了基本技能练，创新拓展练等内容，欢迎下载使用。

一、基本技能练
1.下列说法中，正确的是( )
A.棱柱的侧面可以是三角形
B.若棱柱有两个侧面是矩形，则该棱柱的其他侧面也是矩形
C.正方体的所有棱长都相等
D.棱柱的所有棱长都相等
2.如图所示的等腰梯形是一个几何图形的斜二测直观图，其底角为45°，上底和腰均为1，下底为eq \r(2)＋1，则此直观图对应的平面图形的面积为( )
A.1＋eq \r(2) B.2＋eq \r(2)
C.2＋2eq \r(2) D.4＋2eq \r(2)
3.如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为( )
A.4 B.eq \f(4,3)
C.eq \f(2,3) D.3
4.已知在梯形ABCD中，∠ABC＝eq \f(π,2)，AD∥BC，BC＝2AD＝2AB＝2，则将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )
A.(5＋eq \r(2))π B.(4＋eq \r(2))π
C.(5＋2eq \r(2))π D.(3＋eq \r(2))π
5.如图，位于西安大慈恩寺的大雁塔，是唐代玄奘法师为保存经卷、佛像而主持修建的，是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥，其侧棱与底面所成的角为45°，则该正四棱锥的一个侧面与底面的面积之比为( )
A.eq \r(3)∶2 B.eq \r(2)∶2
C.eq \r(3)∶3 D.eq \r(3)∶4
6.过圆锥的轴作截面，如果截面为正三角形，则称该圆锥为等边圆锥.已知在一等边圆锥中，过顶点P的截面与底面交于CD，若∠COD＝90°(O为底面圆心)，且S△PCD＝eq \f(\r(7),2)，则这个等边圆锥的表面积为( )
A.2π＋eq \r(2)π B.3π
C.2π＋eq \r(3)π D.π＋eq \r(3)π
7.如图，四边形ABCD是边长为2的正方形，ED⊥平面ABCD，FC⊥平面ABCD，ED＝2FC＝2，则四面体ABEF的体积为( )
A.eq \f(1,3) B.eq \f(2,3)
C.1 D.eq \f(4,3)
8.黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值为eq \f(\r(5)－1,2)，约为0.618.这个比例被公认为是最能引起美感的比例，因此被称为黄金比.在几何世界中有很多黄金图形，在三角形中，如果相邻两边之比等于黄金比，且它们夹角的余弦值为黄金比值，那么这个三角形一定是直角三角形，且这个三角形称为黄金分割直角三角形.在正四棱锥中，以黄金分割直角三角形的长直角边作为正四棱锥的高，黄金分割直角三角形的短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离)，斜边作为正四棱锥的斜高，这样得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中，以该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为( )
A.eq \f(\r(5)－1,2) B.eq \f(\r(5)＋1,2)
C.1 D.eq \f(1,4)
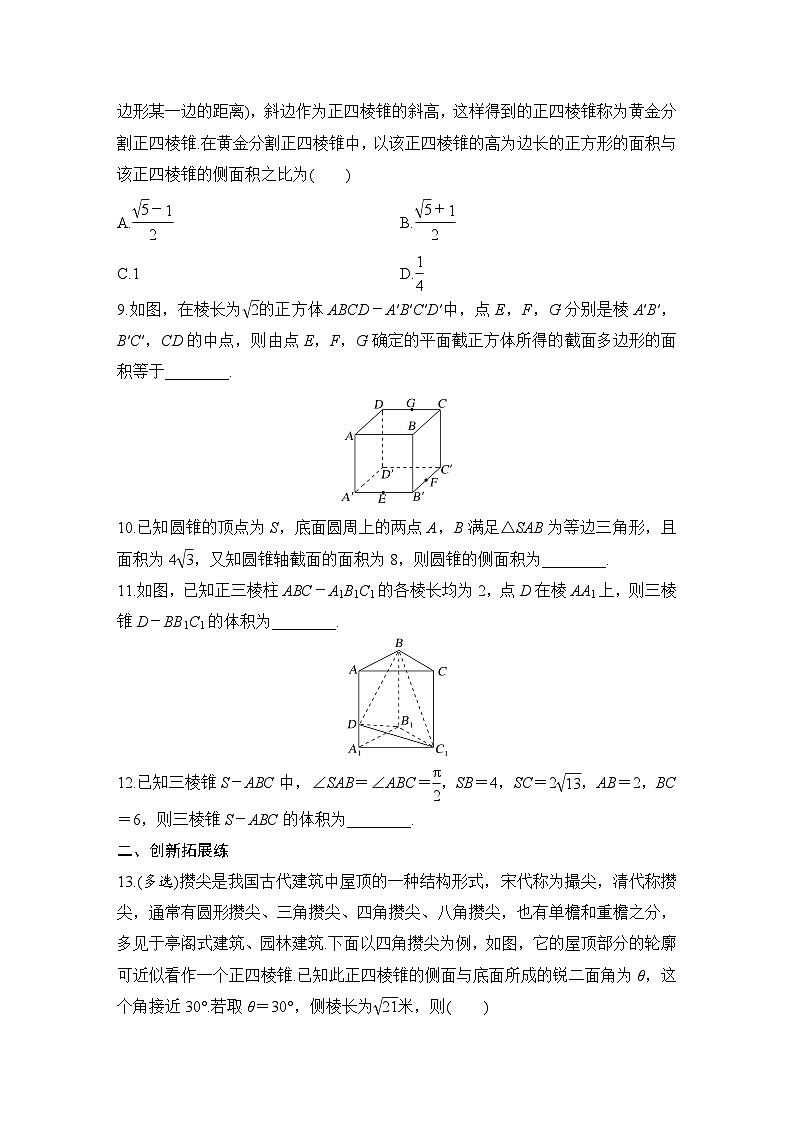
9.如图，在棱长为eq \r(2)的正方体ABCD－A′B′C′D′中，点E，F，G分别是棱A′B′，B′C′，CD的中点，则由点E，F，G确定的平面截正方体所得的截面多边形的面积等于________.
10.已知圆锥的顶点为S，底面圆周上的两点A，B满足△SAB为等边三角形，且面积为4eq \r(3)，又知圆锥轴截面的面积为8，则圆锥的侧面积为________.
11.如图，已知正三棱柱ABC－A1B1C1的各棱长均为2，点D在棱AA1上，则三棱锥D－BB1C1的体积为________.
12.已知三棱锥S－ABC中，∠SAB＝∠ABC＝eq \f(π,2)，SB＝4，SC＝2eq \r(13)，AB＝2，BC＝6，则三棱锥S－ABC的体积为________.
二、创新拓展练
13.(多选)攒尖是我国古代建筑中屋顶的一种结构形式，宋代称为撮尖，清代称攒尖，通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖，也有单檐和重檐之分，多见于亭阁式建筑、园林建筑.下面以四角攒尖为例，如图，它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为θ，这个角接近30°.若取θ＝30°，侧棱长为eq \r(21)米，则( )
A.正四棱锥的底面边长为6米
B.正四棱锥的底面边长为3米
C.正四棱锥的侧面积为24eq \r(3)平方米
D.正四棱锥的侧面积为12eq \r(3)平方米
14.(多选)如图，正方体ABCD－A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF＝eq \f(1,2)，则下列结论中错误的是( )
A.AC⊥AF
B.EF∥平面ABCD
C.三棱锥A－BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
15.(多选)《九章算术》是《算经十书》中最重要的一部，其中将有三条棱互相平行且有一个面为梯形的五面体称为“羡除”，则( )
A.“羡除”有且仅有两个面为三角形
B.“羡除”一定不是台体
C.不存在有两个面为平行四边形的“羡除”
D.“羡除”至多有两个面为梯形
16.(多选)如图，四边形ABCD为正方形，ED⊥平面ABCD，FB∥ED，AB＝ED＝2FB.记三棱锥E－ACD，F－ABC，F－ACE的体积分别为V1，V2，V3，则( )
A.V3＝2V2 B.V3＝V1
C.V3＝V1＋V2 D.2V3＝3V1
参考答案与解析
一、基本技能练
1.答案 C
解析 棱柱的侧面都是平行四边形，选项A错误；
其他侧面可能是平行四边形，选项B错误；
棱柱的侧棱与底面边长并不一定相等，选项D错误；
易知选项C正确.
2.答案 B
解析 ∵平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形，
∴平面图形为直角梯形，且直角腰长为2，上底边长为1，下底边长为eq \r(2)＋1，
∴平面图形的面积S＝eq \f(1＋1＋\r(2),2)×2＝2＋eq \r(2).故选B.
3.答案 B
解析 易知该几何体是由上、下两个全等的正四棱锥组成的，其中正四棱锥底面边长为eq \r(2)，棱锥的高为1，所以该多面体的体积V＝2×eq \f(1,3)×(eq \r(2))2×1＝eq \f(4,3).
4.答案 A
解析 因为在梯形ABCD中，∠ABC＝eq \f(π,2)，AD∥BC，BC＝2AD＝2AB＝2，
所以将梯形ABCD绕AD所在的直线旋转一周得到的几何体是一个底面半径为1，高为2的圆柱挖去一个底面半径为1，高为1的圆锥后剩余的部分，如图所示.
所以该几何体的表面积S＝π×12＋2π×1×2＋π×1×eq \r(12＋12)＝(5＋eq \r(2))π.
5.答案 D
解析 设塔顶是正四棱锥P－ABCD(如图)，PO是正四棱锥的高.
设正四棱锥底面边长为a，则底面面积S1＝a2，
因为AO＝eq \f(\r(2),2)a，∠PAO＝45°，
所以PA＝eq \r(2)×eq \f(\r(2),2)a＝a，
所以△PAB是正三角形，其面积为
S2＝eq \f(\r(3),4)a2，
所以S2∶S1＝eq \f(\r(3),4)a2∶a2＝eq \r(3)∶4.
6.答案 B
解析 如图，连接PO，设圆锥的母线长为2a，则圆锥的底面圆的半径为a，高为PO＝eq \r(3)a.
由已知得CD＝eq \r(2)a，PC＝PD＝2a，
则S△PCD＝eq \f(1,2)×eq \r(2)a×eq \r(（\r(3)a）2＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)a))\s\up12(2))＝eq \f(\r(7),2)，
从而可得a＝1，
圆锥的表面积为πa×2a＋πa2＝3πa2＝3π.
7.答案 B
解析 ∵ED⊥平面ABCD且AD⊂平面ABCD，
∴ED⊥AD.
∵在正方形ABCD中，AD⊥DC，
又DC∩ED＝D，DC，ED⊂平面CDEF，
∴AD⊥平面CDEF.
易知FC＝eq \f(ED,2)＝1，VA－BEF＝VABCDEF－VF－ABCD－VA－DEF.
∵VE－ABCD＝eq \f(1,3)·ED·S正方形ABCD＝eq \f(1,3)×2×2×2＝eq \f(8,3)，
VB－EFC＝eq \f(1,3)·BC·S△EFC＝eq \f(1,3)×2×2×1×eq \f(1,2)＝eq \f(2,3)，
∴VABCDEF＝VE－ABCD＋VB－EFC＝eq \f(8,3)＋eq \f(2,3)＝eq \f(10,3).
又VF－ABCD＝eq \f(1,3)·FC·S正方形ABCD＝eq \f(1,3)×1×2×2＝eq \f(4,3)，
VA－DEF＝eq \f(1,3)·AD·S△DEF＝eq \f(1,3)×2×2×2×eq \f(1,2)＝eq \f(4,3)，
∴VA－BEF＝VABCDEF－VF－ABCD－VA－DEF＝eq \f(10,3)－eq \f(4,3)－eq \f(4,3)＝eq \f(2,3).故选B.
8.答案 D
解析 如图，在黄金分割正四棱锥P－ABCD中，O是正方形ABCD的中心，
PE是正四棱锥的斜高，设OE＝a，则CD＝2a，
∴Rt△POE为黄金分割直角三角形，
则eq \f(OE,PE)＝eq \f(\r(5)－1,2)，
∴PE＝eq \f(\r(5)＋1,2)a，
则PO＝eq \r(PE2－OE2)＝eq \r(\f(1＋\r(5),2))a，
∴以该正四棱锥的高为边长的正方形的面积S＝PO2＝eq \f(1＋\r(5),2)a2，
又正四棱锥的四个侧面是全等的，
∴S侧＝4S△PCD＝4×eq \f(1,2)×CD×PE＝2(1＋eq \r(5))a2，
∴该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为eq \f(1,4).
9.答案 eq \f(3\r(3),2)
解析 分别取AD，CC′和AA′的中点为P，M，N，
可得出过E，F，G三点的平面截正方体所得截面为正六边形EFMGPN，
则正六边形的边长MG＝eq \r(CG2＋CM2)＝eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))\s\up12(2)＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))\s\up12(2))＝1，
故截面多边形的面积S＝6×eq \f(\r(3),4)×12＝eq \f(3\r(3),2).
10.答案 8eq \r(2)π
解析 设圆锥的母线长为l，由△SAB为等边三角形，且面积为4eq \r(3)，
所以eq \f(1,2)l2sin eq \f(π,3)＝4eq \r(3)，
解得l＝4；
又设圆锥底面半径为r，高为h，
则由轴截面的面积为8，得rh＝8；
又r2＋h2＝l2＝16，解得r＝h＝2eq \r(2)，
所以圆锥的侧面积S＝πrl＝π·2eq \r(2)·4＝8eq \r(2)π.
11.答案 eq \f(2\r(3),3)
解析 如图，取BC的中点O，连接AO.
∵正三棱柱ABC－A1B1C1的各棱长均为2，
∴AC＝2，OC＝1，
则AO＝eq \r(3).
∵AA1∥平面BCC1B1，
∴点D到平面BCC1B1的距离为eq \r(3).
又S△BB1C1＝eq \f(1,2)×2×2＝2，
∴VD－BB1C1＝eq \f(1,3)×2×eq \r(3)＝eq \f(2\r(3),3).
12.答案 4eq \r(3)
解析 ∵∠ABC＝eq \f(π,2)，AB＝2，BC＝6，
∴AC＝eq \r(AB2＋BC2)＝eq \r(22＋62)＝2eq \r(10).
∵∠SAB＝eq \f(π,2)，AB＝2，SB＝4，
∴AS＝eq \r(SB2－AB2)＝eq \r(42－22)＝2eq \r(3).
由SC＝2eq \r(13)，得AC2＋AS2＝SC2，
∴AC⊥AS.
又∵SA⊥AB，AC∩AB＝A，AC，AB⊂平面ABC，
∴AS⊥平面ABC.
∴AS为三棱锥S－ABC的高，
∴V三棱锥S－ABC＝eq \f(1,3)×eq \f(1,2)×2×6×2eq \r(3)＝4eq \r(3).
二、创新拓展练
13.答案 AC
解析 如图，在正四棱锥S－ABCD中，O为正方形ABCD的中心，H为AB的中点，
则∠SHO为侧面SAB与底面ABCD所成的锐二面角，
且SH⊥AB，∠SHO＝30°，设底面边长为2a，
所以OH＝AH＝a，OS＝eq \f(\r(3),3)a，
SH＝eq \f(2\r(3),3)a.
在Rt△SAH中，a2＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(3),3)a))eq \s\up12(2)＝21，
解得a＝3，
所以正四棱锥的底面边长为6米，侧面积为S＝eq \f(1,2)×6×2eq \r(3)×4＝24eq \r(3)(平方米).
14.答案 AD
解析 由题意及图形知，当点F与点B1重合时，∠CAF＝60°，故A错误；
由正方体ABCD－A1B1C1D1的两个底面平行，EF⊂平面A1B1C1D1，知EF∥平面ABCD，故B正确；
由几何体的性质及图形知，三角形BEF的面积是定值，点A到平面DD1B1B的距离是定值，故可得三棱锥A－BEF的体积为定值，故C正确；
由图形可以看出，B到直线EF的距离与A到直线EF的距离不相等，故△AEF的面积与△BEF的面积不相等，故D错误.故选AD.
15.答案 ABC
解析 由题意知AE∥BF∥CD，四边形ACDE为梯形，
如图所示.选项A，由题意知“羡除”有且仅有两个面为三角形，故A正确；
选项B，因为AE∥BF∥CD，
所以“羡除”一定不是台体，故B正确；
选项C，假设四边形ABFE和四边形BCDF为平行四边形，
则AE∥BF∥CD，且AE＝BF＝CD，
即四边形ACDE为平行四边形，与已知四边形ACDE为梯形矛盾，故不存在，故C正确；
选项D，若AE≠BF≠CD，则“羡除”有三个面为梯形，故D错误.故选ABC.
16.答案 CD
解析 如图，连接BD交AC于O，连接OE，OF.
设AB＝ED＝2FB＝2，
则AB＝BC＝CD＝AD＝2，FB＝1.
因为ED⊥平面ABCD，FB∥ED，
所以FB⊥平面ABCD，
所以V1＝VE－ACD＝eq \f(1,3)S△ACD·ED＝eq \f(1,3)×eq \f(1,2)AD·CD·ED＝eq \f(1,3)×eq \f(1,2)×2×2×2＝eq \f(4,3)，
V2＝VF－ABC＝eq \f(1,3)S△ABC·FB＝eq \f(1,3)×eq \f(1,2)AB·BC·FB＝eq \f(1,3)×eq \f(1,2)×2×2×1＝eq \f(2,3).
因为ED⊥平面ABCD，AC⊂平面ABCD，所以ED⊥AC，
又AC⊥BD，且ED∩BD＝D，ED，BD⊂平面BDEF，所以AC⊥平面BDEF.
因为OE，OF⊂平面BDEF，
所以AC⊥OE，AC⊥OF.
易知AC＝BD＝eq \r(2)AB＝2eq \r(2)，OB＝OD＝eq \f(1,2)BD＝eq \r(2)，OF＝eq \r(OB2＋FB2)＝eq \r(3)，
OE＝eq \r(OD2＋ED2)＝eq \r(6)，
EF＝eq \r(BD2＋（ED－FB）2)
＝eq \r(（2\r(2)）2＋（2－1）2)＝3，
所以EF2＝OE2＋OF2，所以OF⊥OE.
又OE∩AC＝O，OE，AC⊂平面ACE，
所以OF⊥平面ACE，
所以V3＝VF－ACE＝eq \f(1,3)S△ACE·OF
＝eq \f(1,3)×eq \f(1,2)AC·OE·OF
＝eq \f(1,3)×eq \f(1,2)×2eq \r(2)×eq \r(6)×eq \r(3)＝2，
所以V3≠2V2，V1≠V3，V3＝V1＋V2，2V3＝3V1，所以选项A，B不正确，选项C，D正确.故选CD.