新高考数学一轮复习题型归纳讲义专题05 函数 5.4对数函数（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习题型归纳讲义专题05 函数 5.4对数函数（2份打包，原卷版+解析版），文件包含新高考数学一轮复习题型归纳讲义专题05函数54对数函数原卷版doc、新高考数学一轮复习题型归纳讲义专题05函数54对数函数解析版doc等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。

知识梳理.对数函数
1．对数
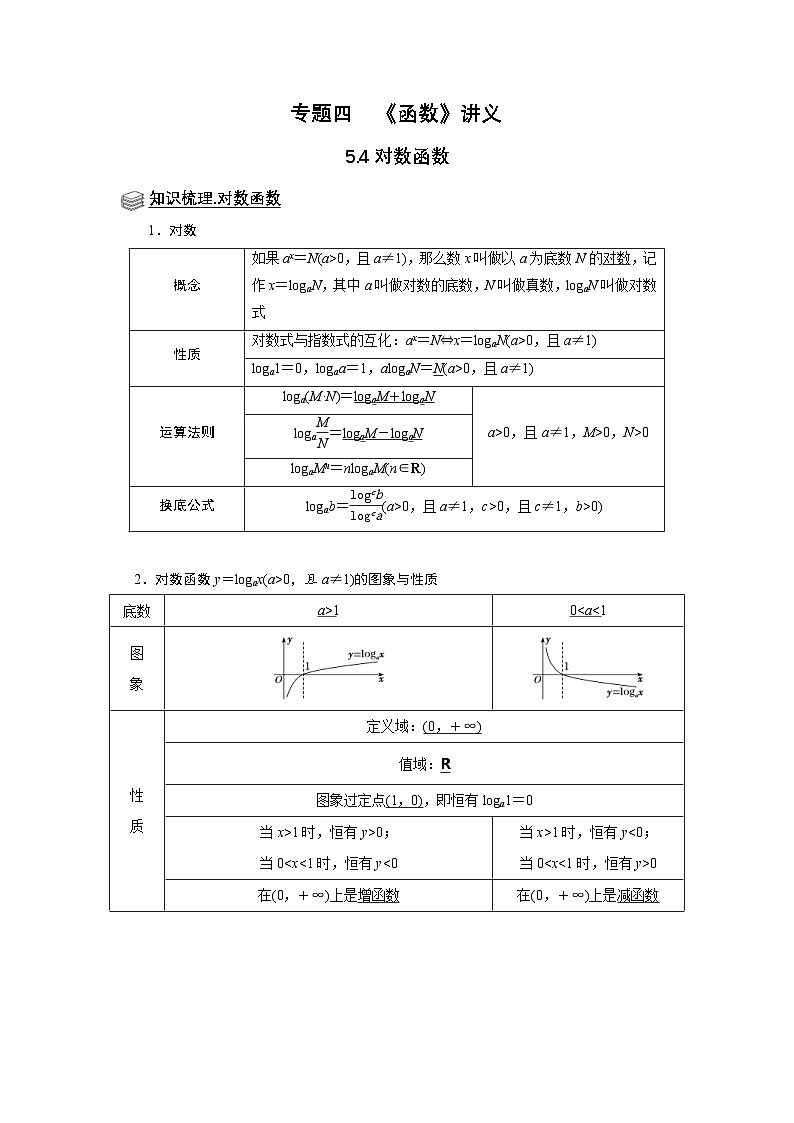
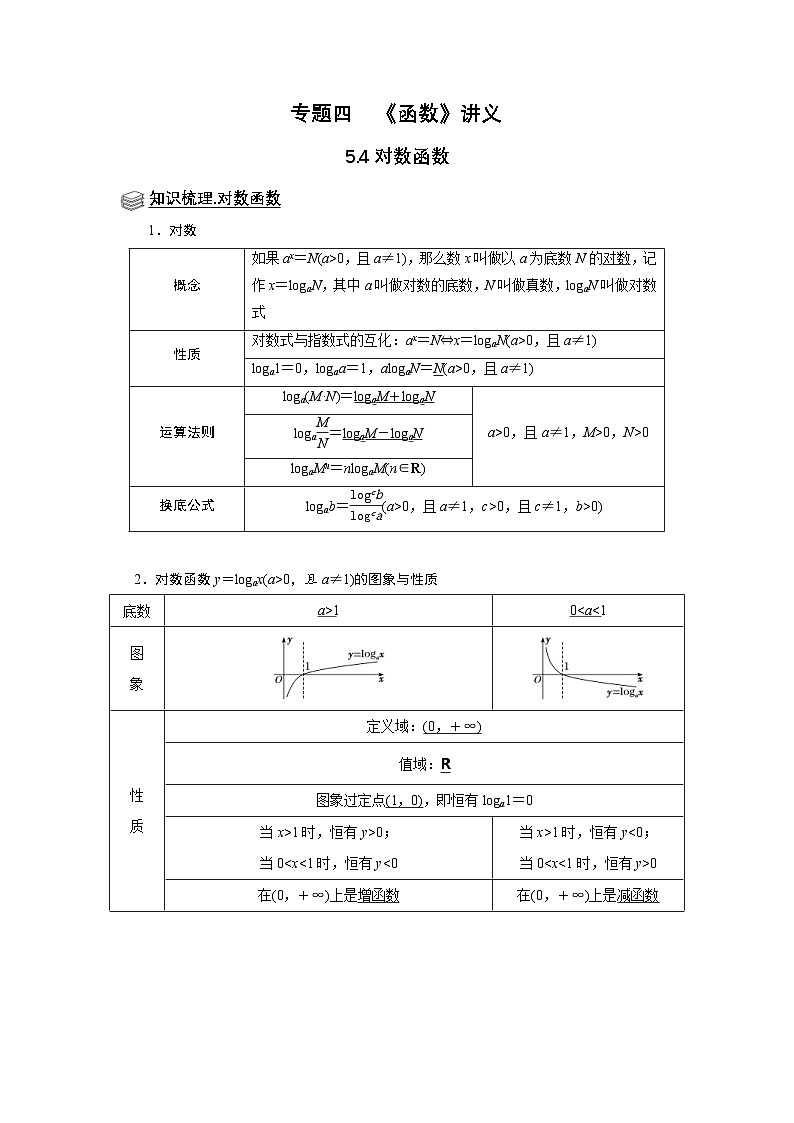
2．对数函数y＝lgax(a>0，且a≠1)的图象与性质
题型一. 指、对运算
1．已知函数f（x），则f（）＝
2．已知函数f（x）满足：x≥4，则f（x）＝2x；当x＜4时f（x）＝f（x+1），则f（23）＝ ．
3．已知a＞b＞1，若lgab+lgba，则a，b的值分别为（ ）
A．a＝5，b＝2B．a＝4，b＝2C．a＝8，b＝4D．
4．设a＝lg0.20.3，b＝lg20.3，则（ ）
A．a+b＜ab＜0B．ab＜a+b＜0C．a+b＜0＜abD．ab＜0＜a+b
题型二. 比较大小
1．（2017秋•信丰县校级月考）设a＝lg32，b＝ln2，c，则a、b、c三个数的大小关系是（ ）
A．a＞b＞cB．b＞a＞cC．c＞a＞bD．c＞b＞a
2．已知a＝lg36，b＝lg510，c＝lg714，则a，b，c的大小关系是（ ）
A．b＜c＜aB．c＜b＜aC．a＜b＜cD．b＜a＜c
3．（2016•新课标Ⅰ）若a＞b＞1，0＜c＜1，则（ ）
A．ac＜bcB．abc＜bac
C．algbc＜blgacD．lgac＜lgbc
4．（2020•新课标Ⅲ）已知55＜84，134＜85．设a＝lg53，b＝lg85，c＝lg138，则（ ）
A．a＜b＜cB．b＜a＜cC．b＜c＜aD．c＜a＜b
5．若，，，则a，b，c的大小关系为（ ）
A．a＞c＞bB．a＞b＞cC．c＞a＞bD．b＞a＞c
6．（2017•新课标Ⅰ）设x、y、z为正数，且2x＝3y＝5z，则（ ）
A．2x＜3y＜5zB．5z＜2x＜3yC．3y＜5z＜2xD．3y＜2x＜5z
题型三. 对数函数的图像与性质
1．已知函数f（x）＝lg（ax2+3x+2）的定义域为R，则实数a的取值范围是 ．
2．（2014•西城区模拟）已知函数f（x）＝lgm（2﹣x）+1（m＞0，且m≠1）的图象恒过点P，且点P在直线ax+by＝1（a＞0，b＞0）上，那么ab的（ ）
A．最大值为B．最小值为C．最大值为D．最小值为
3．（2020春•吉林期末）函数y＝|lg（x+1）|的图象是（ ）
A．B．
C．D．
4．（2008•山东）已知函数f（x）＝lga（2x+b﹣1）（a＞0，a≠1）的图象如图所示，则a，b满足的关系是（ ）
A．0＜a﹣1＜b＜1B．0＜b＜a﹣1＜1
C．0＜b﹣1＜a＜1D．0＜a﹣1＜b﹣1＜1
5．（2020秋•西安月考）已知函数f（x）＝lg，则f（x）是（ ）
A．非奇非偶函数，且在（0，+∞）上单调递增
B．奇函数，且在R上单调递增
C．非奇非偶函数，且在（0，+∞）上单调递减
D．偶函数，且在R上单调递减
题型四. 复合函数的单调性与值域
1．已知函数y＝lga（1﹣ax）在（1，2）上是增函数，则a的取值范围是（ ）
A．（1，2）B．[1，2]C．D．
2．若函数y＝lga（x2﹣ax+2）在区间（﹣∞，1]上为减函数，则a的取值范围是 ．
3．已知函数f（x）＝lg4（ax2﹣4x+a）（a∈R），若f（x）的值域为R，则实数a的取值范围是（ ）
A．[0，2]B．（2，+∞）C．（0，2]D．（﹣2，2）
4．设a＞0，a≠1，函数f（x）＝lga（x2﹣2x+3）有最小值，则不等式lga（x﹣1）＜0的解集（ ）
A．（﹣∞，2）B．（1，2）
C．（2，+∞）D．（1，2）∪（2，+∞）
5．已知函数f（x）＝ln（|x|+1），则使得f（x）＞f（2x﹣1）的x的取值范围是（ ）
A．B．
C．（1，+∞）D．
题型五.等高线
1．已知函数f（x），若a，b，c互不相等，且f（a）＝f（b）＝f（c），则abc的取值范围是（ ）
A．（1，10）B．（5，6）C．（10，12）D．（20，24）
2．已知函数，若关于x的方程f（x）＝a有四个根x1，x2，x3，x4，则这四个根之和x1+x2+x3+x4的取值范围是 ．
题型六.反函数
1．设常数a＞0且a≠1，函数f（x）＝lgax，若f（x）的反函数图象经过点（1，2），则a＝ ．
2．设是奇函数，若函数g（x）图象与函数f（x）图象关于直线y＝x对称，则g（x）的值域为（ ）
A．B．
C．（﹣∞，﹣2）∪（2，+∞）D．（﹣2，2）
3．若x1满足2x＝5﹣x，x2满足x+lg2x＝5，则x1+x2等于（ ）
A．2B．3C．4D．5
课后作业.基本初等函数
1．已知x＝lnπ，yπ，z＝e﹣2，则（ ）
A．x＜y＜zB．y＜x＜zC．y＜z＜xD．z＜y＜x
2．若函数f（x）＝ax（a＞0且a≠1）在R上为减函数，则函数y＝lga（|x|﹣1）的图象可以是（ ）
A．B．
C．D．
3．若函数f（x）＝ax（a＞0，a≠1）在[﹣1，2]上的最大值为4，最小值为m，且函数在[0，+∞）上是增函数，则a＝（ ）
A．B．C．D．
4．已知定义在R上的函数f（x）＝2|x﹣m|﹣1（m为实数）为偶函数，记a＝f（lg0.53），b＝f（lg25），c＝f（2+m），则a，b，c的大小关系为（ ）
A．a＜b＜cB．a＜c＜bC．c＜a＜bD．c＜b＜a
5．已知函数f（x）＝|lgx|，若0＜a＜b且f（a）＝f（b），则a+2b的取值范围为 ．
6．已知函数f（x）＝lga（x+1），g（x）＝lga（1﹣x）（a＞0，a≠1），则（ ）
A．函数f（x）+g（x）的定义域为（﹣1，1）
B．函数f（x）+g（x）的图象关于y轴对称
C．函数f（x）+g（x）在定义域上有最小值0
D．函数f（x）﹣g（x）在区间（0，1）上是减函数
概念
如果ax＝N(a>0，且a≠1)，那么数x叫做以a为底数N的对数，记作x＝lgaN，其中a叫做对数的底数，N叫做真数，lgaN叫做对数式
性质
对数式与指数式的互化：ax＝N⇔x＝lgaN(a>0，且a≠1)
lga1＝0，lgaa＝1，algaN＝N(a>0，且a≠1)
运算法则
lga(M·N)＝lgaM＋lgaN
a>0，且a≠1，M>0，N>0
lgaeq \f(M,N)＝lgaM－lgaN
lgaMn＝nlgaM(n∈R)
换底公式
lgab＝eq \f(lgcb,lgca)(a>0，且a≠1，c>0，且c≠1，b>0)
底数
a>1
0图
象
性
质
定义域：(0，＋∞)
值域：R
图象过定点(1，0)，即恒有lga1＝0
当x>1时，恒有y>0；
当0当x>1时，恒有y<0；
当00
在(0，＋∞)上是增函数
在(0，＋∞)上是减函数