新高考数学一轮复习百题刷过关专题25 圆锥曲线压轴小题必刷100题（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习百题刷过关专题25 圆锥曲线压轴小题必刷100题（2份打包，原卷版+解析版），文件包含新高考数学一轮复习百题刷过关专题25圆锥曲线压轴小题必刷100题原卷版doc、新高考数学一轮复习百题刷过关专题25圆锥曲线压轴小题必刷100题解析版doc等2份试卷配套教学资源，其中试卷共131页， 欢迎下载使用。

1．已知圆是以点和点为直径的圆，点为圆上的动点，若点，点，则的最大值为（ ）
A．B．C．D．
【答案】A
【分析】
由题设可知圆：，在坐标系中找到，应用三角线相似将转化到，再利用三角形的三边关系确定目标式的最大值即可.
【详解】
由题设，知：且，即圆的半径为4，
∴圆：，
如上图，坐标系中则，
∴，即△△，故，
∴，在△中，
∴要使最大，共线且最大值为的长度.
∴.
故选：A
2．已知点，分别为椭圆的左、右焦点，点在直线上运动，若的最大值为，则椭圆的离心率是（ ）
A．B．C．D．
【答案】C
【分析】
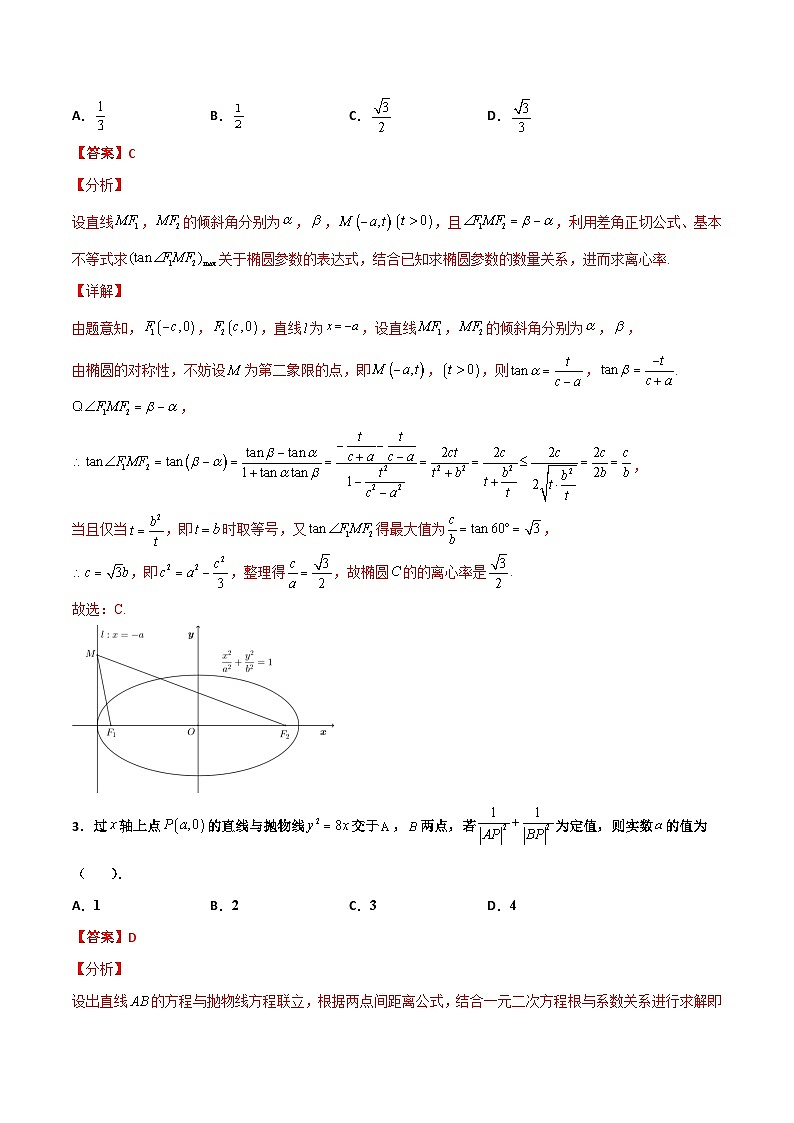
设直线，的倾斜角分别为，，，且，利用差角正切公式、基本不等式求关于椭圆参数的表达式，结合已知求椭圆参数的数量关系，进而求离心率.
【详解】
由题意知，，，直线为，设直线，的倾斜角分别为，，
由椭圆的对称性，不妨设为第二象限的点，即，，则，.
，
，
当且仅当，即时取等号，又得最大值为，
，即，整理得，故椭圆的的离心率是.
故选：C.
3．过轴上点的直线与抛物线交于，两点，若为定值，则实数的值为（ ）．
A．1B．2C．3D．4
【答案】D
【分析】
设出直线的方程与抛物线方程联立，根据两点间距离公式，结合一元二次方程根与系数关系进行求解即可.
【详解】
设直线的方程为，
代入，得，
设，，则，．
，
同理，，
∴
，
∵为定值是与无关的常数，
∴，
故选：D．
4．已知椭圆：的两个顶点在直线上，，分别是椭圆的左､右焦点，点是椭圆上异于长轴两个端点的任一点，过点作椭圆的切线与直线交于点，设直线，的斜率分别为，，则的值为（ ）
A．-B．C．-D．-
【答案】A
【分析】
根据题意求出，，进而写出椭圆的方程，设点的切线方程为，与椭圆联立，由得到，然后依次表示出相关点的坐标，利用斜率公式表示出，进而化简整理即可求出结果.
【详解】
∵椭圆的两顶点在直线上，∴，，∴椭圆的方程为，∴，，设点的切线方程为，，联立，消去得，∵直线与椭圆相切，∴，即，∴，，∴，∴点，又，∴，∴，设点，又在切线上，∴，∴，∴，
故选：A.
5．已知F是椭圆的左焦点，A是该椭圆的右顶点，过点F的直线l（不与x轴重合）与该椭圆相交于点M，N．记，设该椭圆的离心率为e，下列结论正确的是（ ）
A．当时，B．当时，
C．当时，D．当时，
【答案】A
【分析】
设在轴上方，在轴下方，设直线的倾斜角为，直线的倾斜角为，联立直线的方程与椭圆方程可求的坐标，同理可求的坐标，利用三点共线可得，利用离心率的范围可得，从而可判断为锐角.
【详解】
不失一般性，设在轴上方，在轴下方，
设直线的斜率为，倾斜角为，直线的斜率为，倾斜角为，
则，，，且.
又.
又直线的方程为，
由可得，
故，所以，故，
同理，故，
因为共线，故，
整理得到即，
若，，
因为，，故，所以，
故.
故选：A.
6．已知过抛物线的焦点的直线与抛物线交于点、，若、两点在准线上的射影分别为、，线段的中点为，则下列叙述不正确的是（ ）
A．B．四边形的面积等于
C．D．直线与抛物线相切
【答案】B
【分析】
对于选项AB，利用向量知识研究与､与的位置关系即可；对于选项C，可利用抛物线的定义确定、的长度，然后判断等号是否成立；对于选项D，求出直线的斜率，并设抛物线在点处的切线方程为，与抛物线的方程联立，由求出，进而可判断出D选项的正误.
【详解】
如图，由题意可得，抛物线的准线方程为．
设、，设直线的方程为，
联立，可得，利用根与系数的关系得，
因为线段的中点为，所以，
所以，，
所以，，
所以，，A选项正确；
对于B选项，因为，所以，
所以，所以，
所以四边形的面积等于，B选项错误；
对于C选项，根据抛物线的定义知，，
所以，
，
所以，，C选项正确；
对于D选项，直线的斜率为，
抛物线在点处的切线方程为，
联立，消去可得，
由题意可得，可得，即，则.
所以，直线与抛物线相切，D选项正确.
故选：B.
7．如图，已知双曲线的左、右焦点分别为，，过右焦点作平行于一条渐近线的直线交双曲线于点，若的内切圆半径为，则双曲线的离心率为（ ）
A．B．
C．D．
【答案】A
【分析】
设双曲线的左、右焦点分别为，，设双曲线的一条渐近线方程为，可得直线的方程为，联立双曲线的方程可得点的坐标，设，，运用三角形的等面积法，以及双曲线的定义，结合锐角三角函数的定义，化简变形可得关于，的方程，结合离心率公式可得所求值．
【详解】
设双曲线的左、右焦点分别为，，
设双曲线的一条渐近线方程为，
可得直线的方程为，与双曲线联立，
可得，，
设，，
由三角形的等面积法可得，
化简可得，①
由双曲线的定义可得，②
在三角形中，为直线的倾斜角），
由，，可得，
可得，③
由①②③化简可得，
即为，
可得，则．
故选：A．
8．在棱长为的正四面体中，点为所在平面内一动点，且满足，则的最大值为（ ）
A．B．C．D．
【答案】B
【分析】
由题意可知，点在所在平面内的轨迹为椭圆，且该椭圆的焦点为、，长轴长为，然后以线段的中点为坐标原点，直线所在直线为轴，以所在直线为轴建立空间直角坐标系，求出椭圆的方程，利用二次函数的基本性质可求得的最大值.
【详解】
如图所示，在平面内，，
所以点在平面内的轨迹为椭圆，取的中点为点，连接，以直线为轴，直线为建立如下图所示的空间直角坐标系，
则椭圆的半焦距，长半轴，该椭圆的短半轴为，
所以，椭圆方程为.
点在底面的投影设为点，则点为的中心，，
故点正好为椭圆短轴的一个端点，
，则，
因为，故只需计算的最大值.
设，则，
则，
当时，取最大值，
即，
因此可得，故的最大值为.
故选：B.
9．已知点为抛物线的焦点，，点为抛物线上一动点，当最小时，点恰好在以，为焦点的双曲线上，则该双曲线的渐近线的斜率的平方为（ ）
A．B．C．D．
【答案】B
【分析】
作出图形，可知与抛物线相切时，取得最小值，求出点的坐标，利用双曲线定义求出2a，结合，可求得，再利用求得结果.
【详解】
由抛物线的对称性，设为抛物线第一象限内点，如图所示：
故点作垂直于抛物线的准线于点B，由抛物线的定义知，易知轴，可得
当取得最大值时，取得最小值，此时与抛物线相切，
设直线方程为：，
联立，整理得，
其中，解得：，由为抛物线第一象限内点，则
则，解得：，此时，即或
所以点的坐标且
由题意知，双曲线的左焦点为，右焦点为
设双曲线的实轴长为2a，则，，
又，则
故渐近线斜率的平方为
故选：B
10．已知，为双曲线的左、右焦点，以为直径的圆与双曲线右支的一个交点为P，与双曲线相交于点Q，且，则该双曲线的离心率为（ ）
A．B．C．D．
【答案】B
【分析】
设则，由及，求a、t的数量关系，可得双曲线参数的齐次方程，即可求双曲线的离心率.
【详解】
设，则，而，
∴，，
由，则，，
∴，解得，则，
∴.
故选：B
11．若椭圆上的点到右准线的距离为，过点的直线与交于两点，且，则的斜率为
A．B．C．D．
【答案】B
【分析】
点代入椭圆方程，点到准线距离和，解得，由，得，联立直线与椭圆方程得到，联立消去即可求出
【详解】
解：由题意可得，解得，
所以椭圆，
设：,设
因为，所以
由得
则结合，联立消去解得
故选：B.
12．已知双曲线：的左焦点为，过原点的直线与双曲线的左、右两支分别交于，两点，则的取值范围是（ ）
A．B．C．D．
【答案】B
【分析】
设，，则，构造函数，，用导数求在上的取值范围即可.
【详解】
设，则.
设双曲线的右焦点为，由对称性可知，则，
所以.令，，
则，令得，
当时，，单调递减；当时，，单调递增.
所以，又当时，所以.
故的取值范围是.
故选：B.
13．已知双曲线（，）的左、右焦点分别为，，点，分别在双曲线的左、右两支上，点在轴上，且，，三点共线，若，，则双曲线的离心率为（ ）
A．B．C．3D．
【答案】B
【分析】
根据平面向量共线的性质，结合双曲线的定义、等边三角形的判定及性质、余弦定理、双曲线的离心率公式进行求解即可.
【详解】
依题意，得，，故；又，故；不妨设，由双曲线的定义可得，，，故，故，则，故为等边三角形，故在中，，即，，，由余弦定理，，则，
故选：B．
14．已知抛物线，为的焦点，过焦点且倾斜角为的直线与交于，两点，则下面结论不正确的是（ ）
A．以，为直径的圆与抛物线的准线相切
B．
C．过点，分别作抛物线的切线，则两切线互相垂直
D．记原点为，则
【答案】D
【分析】
根据抛物线和过焦点的直线的位置关系，联立抛物线方程和直线方程，结合韦达定理和焦点弦公式，逐个判断即可得解.
【详解】
由题意知，令直线，，，
与抛物线联立方程，消去得，
由韦达定理知：，，
如图所示，过，分别作抛物线准线的垂线，垂足分别为，，
记的中点为，过作抛物线准线的垂线，垂足为，
由，
所以以为直径的圆与抛物线的准线相切，故A正确；
由，
所以可得：
，故B正确；
由图，抛物线在第一象限的解析式为，
所以，
所以过点抛物线的切线的斜率为，
同理过点抛物线的切线的斜率为，
所以，所以两切线垂直，故C正确；
由，所以可得：
；
如图，作垂直于，
则，
当时，经检验亦成立，故D错误，
故选：D.
15．已知点是抛物线的对称轴与准线的交点，点为抛物线的焦点，过作抛物线的一条切线，切点为，且满足，则抛物线的方程为（ ）
A．B．C．D．
【答案】C
【分析】
本题首先可根据题意得出点，然后设切线方程为、切点为，通过联立抛物线与切线方程解得，最后对、两种情况分别进行讨论，通过即可得出结果.
【详解】
由题意可知，抛物线准线方程为，点，切线斜率一定存在，
设过点与抛物线相切的直线方程为，切点，
联立抛物线与切线方程，转化得，
，解得，
当时，直线方程为，
，解得，则，
因为，所以，解得；
当时，同理得，
综上所述，抛物线方程为，
故选：C.
16．过点斜率为正的直线交椭圆于，两点.，是椭圆上相异的两点，满足，分别平分，.则外接圆半径的最小值为（ ）
A．B．C．D．
【答案】D
【分析】
分析可知，P，C，D在一个阿波罗尼斯圆上，设其半径为r，且，分直线AB斜率存在及不存在两种情况分别讨论得解．
【详解】
如图，
先固定直线AB，设，则，其中为定值，
故点P，C，D在一个阿波罗尼斯圆上，且外接圆就是这个阿波罗尼斯圆，设其半径为r，阿波罗尼斯圆会把点A，B其一包含进去，这取决于BP与AP谁更大，不妨先考虑的阿波罗尼斯圆的情况，BA的延长线与圆交于点Q，PQ即为该圆的直径，如图：
接下来寻求半径的表达式，
由，解得，
同理，当时有，，
综上，；
当直线AB无斜率时，与椭圆交点纵坐标为，则；
当直线AB斜率存在时，设直线AB的方程为，即，
与椭圆方程联立可得，
设，，则由根与系数的关系有，，
，
注意到与异号，故，
设，则，，当，即，此时，故，
又，综上外接圆半径的最小值为.
故选：D．
17．已知点P在抛物线上，过点P作抛物线的切线，，切点分别为M，N，若，且，则C的准线方程为（ ）
A．B．C．D．
【答案】A
【分析】
设，利用导数写出切线的方程，联立求出交点坐标 ， 又由，知为三角形的重心，代入重心坐标公式，利用已知条件可求出的坐标为再代入抛物线方程, 求出，进而求C的准线方程.
【详解】
设，由，得，则，
则 即
同理直线的方程为 ，
联立的方程可得，则，
又由，得为三角形的重心,
则， ，得，
则，又抛物线上，得，即，
准线方程为.
故选：A.
18．已知点P（－1，0），设不垂直于x轴的直线l与抛物线y2＝2x交于不同的两点A、B，若x轴是∠APB的角平分线，则直线l一定过点
A．（，0）B．（1，0）C．（2，0）D．（-2，0）
【答案】B
【分析】
根据抛物线的对称性，分析得出直线过的顶点应该在x轴上，再设出直线的方程，与抛物线方程联立，设出两交点的坐标，根据角分线的特征，得到所以AP、BP的斜率互为相反数，利用斜率坐标公式，结合韦达定理得到参数所满足的条件，最后求得结果.
【详解】
根据题意，直线的斜率不等于零，并且直线过的定点应该在x轴上，
设直线的方程为，与抛物线方程联立，消元得，
设，因为x轴是∠APB的角平分线，
所以AP、BP的斜率互为相反数，所以，
结合根与系数之间的关系，整理得出，
即，，解得，所以过定点，
故选B.
19．已知 是椭圆与双曲线的公共焦点，P 是它们的一个公共点，且| PF2 || PF1 |，椭圆的离心率为，双曲线的离心率为，，则的最小值为（ ）
A．4B．6C．D．8
【答案】D
【分析】
由题意可得，再设椭圆和双曲线得方程，再利用椭圆和双曲线的定义和离心率可得的表达式，化简后再用均值不等式即可求解.
【详解】
由题意得：，设椭圆方程为，
双曲线方程为，
又∵.
∴，∴，
则

，当且仅当，
即时等号成立.
则的最小值为8.
故选：D
20．已知，分别为双曲线的左，右焦点，过且倾斜角为锐角的直线与双曲线的右支交于，两点，记的内切圆半径为，的内切圆半径为，若，则的值为（ ）
A．B．C．D．
【答案】D
【分析】
根据题意作出示意图，先证焦点三角形内切圆圆心的横坐标均为，再根据角度关系结合半径关系，即可求得结果.
【详解】
如图，记的内切圆圆心为，
内切圆在边、、上的切点分别为、、，
易知、两点横坐标相等，，，，
由，即，
得，即，
记点的横坐标为，则，
则，得.
记的内切圆圆心为，同理得内心的横坐标也为则轴，
由题意知，，
在中，，
在中，，
所以，即，
所以，
故选：D.
21．如图，椭圆，是直线上一点，过点作椭圆的两条切线，，直线与交于点，则的最小值是（ ）
A．B．C．D．
【答案】A
【分析】
先证明过椭圆上点处的切线方程是，这样只要设，可得切线方程，由切线过可得直线方程，得直线过左焦点，可证明，由直线方程与方程联立可解得交点坐标，计算，可得，再由不等式的性质得出最小值．
【详解】
设
若在椭圆的上半部分，则得，
在椭圆上，，
．
∴过点的切线方程是，，即，
同理可证当在下半圆时，过的切线方程也是，是椭圆的左右顶点时，切线方程也是．
∴无论在椭圆的何处，切线方程都是．
设，则过点的切线方程是，
在直线，设，则由两切线都过点
∴，∴直线方程是，易知直线过定点，该定点为椭圆左焦点．
直线方程为，则由，得，即，
，，，∴，
，，
∴
．当且仅当，即时等号成立．
故选：A．
22．已知抛物线，焦点为，圆，过的直线与交于、两点（点在第一象限），且，直线与圆相切，则（ ）
A．B．C．D．
【答案】B
【分析】
设点、，可得，且，由结合向量的坐标运算以及可求得点的坐标，进而可求得直线的方程，由直线与圆相切，得出圆心到直线的距离等于圆的半径，由此可求得实数的值.
【详解】
抛物线的焦点为，设点、，则，且，
由得，，
由，即，即，可得，，
所以，点的坐标为，
直线的斜率为，则直线的方程为，即，
将圆的方程写为标准式得，则，可得.
由于直线与圆相切，则，解得，合乎题意.
故选：B.
23．已知A，B，C为抛物线上不同的三点，焦点F为的重心，则直线与y轴的交点的纵坐标t的取值范围是（ ）
A．B．
C．D．
【答案】C
【分析】
根据题意，设出直线的方程，与抛物线方程联立，利用韦达定理，结合三角形重心的性质，结合题意，求得结果.
【详解】
设，由抛物线的焦点的坐标为，
焦点F为的重心，
所以，
显然直线斜率存在，设为，则直线方程为，
联立，消去得：，
所以，即①，且，
所以，
代入式子得，
又点也在抛物线上，所以，即②，
由①②及可解得，即，
又当时，直线过点，此时三点共线，
由焦点F为的重心，得与共线，
即点也在直线上，此时点与之一重合，
不满足点为该抛物线上不同的三点，所以，
所以实数的取值范围为，
故选：C.
24．已知、是椭圆的左、右焦点，点是椭圆上任意一点，以为直径作圆，直线与圆交于点（点不在椭圆内部），则
A．B．4C．3D．1
【答案】C
【分析】
利用向量的数量积运算可得，利用，进一步利用椭圆的定义可转化为，进而得解.
【详解】
连接,设椭圆的基本量为，
,
故答案为：3.
25．已知双曲线：的右焦点为，和为双曲线上关于原点对称的两点，且在第一象限.连结并延长交于，连结，，若是以为直角的等腰直角三角形，则双曲线的离心率为（ ）
A．B．C．D．
【答案】C
【分析】
如图所示，连接有关各点，根据题意可设,为矩形,根据双曲线的定义得到,,, 在和中，利用勾股定理列出方程组，消去得到得到的关系，进而求得离心率.
【详解】
如图所示，连接有关各点，根据题意可设,
为矩形，且,,,
在和中，
，
由（2）化简得，代入（1）化简得，
故选：C.
26．已知是椭圆的一个焦点，若直线与椭圆相交于两点，且，则椭圆离心率的取值范围是（ ）
A．B．C．D．
【答案】A
【分析】
将与椭圆的左、右焦点连接起来，由椭圆的对称性得到一个平行四边形，利用椭圆的定义和余弦定理，结合重要不等式可得离心率的范围.
【详解】
如图设分别为椭圆的左、右焦点，设直线与椭圆相交于，连接.
根据椭圆的对称性可得：四边形为平行四边形.
由椭圆的定义有：
由余弦定理有：
即
所以
当且仅当时取等号，又的斜率存在，故不可能在轴上.
所以等号不能成立,即即，所以
故选：A
27．已知双曲线的左、右焦点分别为F1，F2，过F2且斜率为的直线与双曲线在第一象限的交点为A，若，则此双曲线的标准方程可能为（ ）
A．x21B．
C．D．
【答案】D
【分析】
由向量的加减运算和数量积的性质，可得，由双曲线的定义可得，再由三角形的余弦定理，可得，，即可判断出所求双曲线的可能方程．
【详解】
解：由题可知，，
若，即为，
可得，即有，
由双曲线的定义可知，
可得，
由于过F2的直线斜率为，
所以在等腰三角形中，，
则，
由余弦定理得：，
化简得：，
即，，
可得，，
所以此双曲线的标准方程可能为：.
故选：D．
28．已知椭圆，，，过点的直线与椭圆交于，，过点的直线与椭圆交于，，且满足，设和的中点分别为，，若四边形为矩形，且面积为，则该椭圆的离心率为（ ）．
A．B．C．D．
【答案】D
【分析】
画出图像，由面积和勾股定理列式可得，，在中，有长度关系可得，从而得和，再利用点差法得，从而可求得离心率．
【详解】
如图，不妨设，两条直线的斜率大于零时，连结，
由题意知，
解得，，或，（舍）
，，
在中，因为，所以，
故此时，．
设，，则，
两式相减得，
即，即，
因此离心率，所以，故选D．
29．已知单位向量，满足，若存在向量，使得，则的取值范围是（ ）
A．B．C．D．
【答案】C
【分析】
由题意,设向量,的夹角为,由化简求得，设,则,由化简可知即在以为圆心,半径为1的圆上,由点与圆的位置关系分析可得即可得答案.
【详解】
根据题意,设向量,的夹角为,若,
则,
即,解得:.
则在直角坐标系中,设,
则,
则有,若,
则有,
即,
变形可得: ,
点C在以为圆心,半径为1的圆上,设,
则,则有,
则有,
所以的取值范围是
故选:C.
30．设双曲线的左、右焦点分别为，过的直线分别与双曲线左右两支交于两点，以为直径的圆过，且，则直线的斜率为（ ）
A．B．C．D．
【答案】B
【分析】
根据圆的性质得到，根据得到.设为的中点.根据双曲线的定义和等腰直角三角形的性质，结合勾股定理列方程，求得，以及，进而求得直线的斜率.
【详解】
由为直径的圆过，所以，由，得，即，即，即，所以，所以.设，则，由，，两式相加可得，即有，设为的中点，在直角三角形中可得，化为，即，而，所以，所以直线的斜率为.
故选：B
31．已知抛物线，F是抛物线C的焦点，M是抛物线C上一点，O为坐标原点，，的平分线过FM的中点，则点M的坐标为（ ）
A．B．C．D．
【答案】A
【分析】
设线段FM的中点为Q，作轴于点N，轴于点，交C的准线l于点，
则，故,过点Q作于点T,可得重合，设可得出的坐标满足，再与抛物线方程联立，可求出的坐标.
【详解】
设线段FM的中点为Q，作轴于点N，轴于点，交C的准线l于点，
则，故.
过点Q作于点T，由是的角平分线.
则，由垂线段的唯性知，重合，
可得，则M在以线段PF为直径的圆上.设，
则由，得，将代入得
，易知，所以，即，
得，所以.故M的坐标为.
故选：A
32．已知是椭圆上的两个动点，，则以为直角顶点的等腰直角的个数为（ ）
A．B．C．D．多于
【答案】A
【分析】
当轴时，易得有两个满足条件的三角形，当不垂直于x轴时，通过分析可知点从左顶点运动到右顶点的过程中，是逐渐减小的，可得此种情况没有满足题意的等腰直角三角形.
【详解】
当轴时，如图所示，显然有两个满足条件的三角形.
当不垂直于x轴时，不妨假设，，
，由复合函数的单
调性知，在上单调递减，所以点从左顶点运动到右顶点的
过程中，不存在另一个异于的点，使得.综上，满足条件的三角形只有
2个.
故选：A.
33．在平面直角坐标系中，圆，若圆上存在以为中点的弦，且，则实数的取值范围是
A．B．C．D．
【答案】C
【分析】
本题的实质是圆上存在两点，使.若，为切线，则可求得.过向圆引的两条切线的夹角不小于时，，进而求得答案.
【详解】
为的中点，且，
为直角三角形，，
若，为切线，且，则，
在中，，，，
则，
过点向圆引的两条切线的夹角不小于时，满足题意，
则圆心到的距离不大于，
即，解得.
故选：C.
34．已知椭圆，过x轴上一定点N作直线l，交椭圆C于A，B两点，当直线l绕点N任意旋转时，有（其中t为定值），则（ ）
A．B．C．D．
【答案】B
【分析】
设点,当直线与轴不重合时,设的方程为,代入椭圆方程,化简得 ,利用韦达定理化简得,因为为定值,特殊值代入即可求得,进而求得定值.
【详解】
设点
当直线与轴不重合时,设的方程为,代入椭圆方程,得: ,即.
当直线l绕点N任意旋转时，有（其中t为定值）,
当时,
当时,
,
解得: 代入当时, .
故选:B.
35．已知圆与圆，过动点分别作圆、圆的切线，，（分别为切点），若，则的最小值是
A．5B．C．D．
【答案】D
【分析】
P的轨迹为线段的中垂线：，
由，得到的最小值是点到直线的距离的平方，由此能求出结果．
【详解】
∵圆与圆，
∴，，
∵过动点分别作圆、圆的切线，，（，分别为切点），，
∴P的轨迹为线段的中垂线，线段的中点坐标为，
线段的斜率，的中垂线所在直线的斜率为，
∴P的轨迹方程为，即，
∵表示点与距离的平方，
∴的最小值是点到直线的距离的平方，
∴的最小值为：．
故选：D．
36．已知抛物线，过点的直线与交于不同的两点，，且满足，以为中点的线段的两端点分别为，其中在轴上，在上，则的最小值为
A．B．C． D．
【答案】D
【分析】
设出直线方程，联立抛物线方程，根据韦达定理求得；设出方程，利用韦达定理，将目标式转化为关于未知量的函数，求函数值域即可求得结果.
【详解】
设的方程为，代入，得，
所以，，可得.
设直线方程为，
，同理得，，
所以，
又为中点，所以，即.所以，
所以
，令，则，其对称轴，
故当且仅当时取得最小值.
故当，即轴时，最小，最小值为.
故选：D.
37．设抛物线的焦点为F，过F的两条直线，分别交抛物线于点A，B，C，D，且，的斜率，满足，若的最小值为30，则抛物线的方程为
A．B．C．D．
【答案】B
【分析】
设，，联立直线的方程和抛物线的方程消元，然后韦达定理可得，，然后利用弦长公式可算出，同理，然后可得，然后利用导数求出的最小值，然后即可求出
【详解】
由题意可得直线的方程为：，与联立得
.
设，，
所以，，
所以，
同理可得，
所以.
令，，
则，
当时，，
则在上单调递减，
当时，，
则在上单调递增.
所以当时，，
所以，，
所以抛物线的解析式为.
故选：B.
38．设点为椭圆上一点，、分别是椭圆的左、右焦点，且的重心为点，如果，那么的面积为（ ）
A．B．C．D．
【答案】C
【分析】
由题设条件及椭圆的定义，可得，进而可得为等腰三角形，计算，由重心和中点的定义，，即得解
【详解】
由于点P为椭圆上一点，
又
故为等腰三角形，以为底的高为：
故

故选：C
39．过双曲线的右焦点作直线，且直线与双曲线的一条渐近线垂直，垂足为，直线与另一条渐近线交于点，已知为坐标原点，若的内切圆的半径为，则双曲线的离心率为（ ）
A．B．C．D．或2
【答案】D
【分析】
分在轴同侧和在轴异侧两种情况进行求解：不妨设在第一象限，根据题意作出图形，利用图形中的几何关系求出的值，再由离心率求解即可.
【详解】
有两种情况：
（1）若在轴同侧，不妨设在第一象限.如图，
设内切圆的圆心为，则在的平分线上，
过点分别作于，于，
由得四边形为正方形，利用点到直线的距离公式可得，
焦点到渐近线的距离为，
又，所以，
又，
所以，
所以，
从而可得离心率；
（2）若在轴异侧，不妨设在第一象限如图，
易知，，，
因为的内切圆半径为，
所以，
又因为，
所以，，
所以，，
则，
从而可得离心率.
综上，双曲线的离心率为或2.
故选：D
40．已知为抛物线的焦点，点都是抛物线上的点且位于轴的两侧，若(为原点)，则和的面积之和的最小值为（）
A．B．C．D．
【答案】A
【分析】
首先设出直线方程，代入抛物线方程，利用根系关系及平面向量数量积坐标公式得到，再计算和的面积之和，利用均值不等式求其最小值即可.
【详解】
设直线的方程为，，，
.
，
解得：或.
因为位于轴的两侧，所以.
即：，.
设点在轴的上方，则，，.
当且仅当时，即时，取“”号.
所以和的面积之和的最小值为.
故选：A
二、多选题
41．在平面直角坐标系中，已知抛物线的焦点为，准线为，过点且斜率大于0的直线交抛物线于，两点(其中在的上方)，过线段的中点且与轴平行的直线依次交直线，，于点，，.则（ ）
A．
B．若，是线段的三等分点，则直线的斜率为
C．若，不是线段的三等分点，则一定有
D．若，不是线段的三等分点，则一定有
【答案】AB
【分析】
设直线方程为，，直线方程代入抛物线方程应用韦达定理得，从而可表示出点坐标，然后求出点坐标，判断各选项．
【详解】
抛物线的焦点为，准线
设直线方程为，，，
联立，消去y得，
由韦达定理得：，，
∴，，直线方程为，
对于A，∵共线，∴，，同理，
，，
∴，即，故A正确；
对于B，若P，Q是线段的三等分点，则，，即，
又，，
∴，∴，又，解得：，故B正确；
对于C，由得，，
，，∴，
又，∴，
当时，，故C错；
对于D，由图可知，而，只要，就有，故D错．
故选：AB．
42．已知双曲线的左､右焦点分别为，，O为坐标原点，圆，P是双曲线C与圆O的一个交点，且，则下列结论中正确的有（ ）
A．双曲线C的离心率为
B．点到一条渐近线的距离为
C．的面积为
D．双曲线C上任意一点到两条渐近线的距离之积为2
【答案】ABD
【分析】
由双曲线及圆的方程知圆O的半径为c，所以，又，根据双曲线的定义、勾股定理、双曲线中的关系得双曲线C的方程为：，从而可判断选项A正确；求出双曲线的渐近线方程，由点到直线的距离公式可判断选项B、D正确；由面积公式可判断选项C错误.
【详解】
解：∵双曲线，
∴，
又圆，
∴圆O的半径为c，
∴为圆O的直径，∴，
故作图如下：
对于A，∵，∴，
∴，令，则，
∴，
∴，又，
∴双曲线C的离心率，故A正确；
对于B，由于到渐近线的距离，故B正确；
对于C，由离心率得，，
∴，
∴，，
∴的面积为，故C错误；
对于D，由得双曲线C的方程为：，
故其两条渐近线方程为，即，
设为双曲线C上任意一点，则，即①，
到两条渐近线的距离，，
∴，故D正确；
故选：ABD.
43．曼哈顿距离(或出租车几何)是由十九世纪的赫尔曼·闵可夫斯基所创的词汇，是一种使用在几何度量空间的几何学用语.例如，在平面上，点和点的曼哈顿距离为：.若点为上一动点，为直线上一动点，设为，两点的曼哈顿距离的最小值，则的可能取值有（ ）
A．B．C．D．
【答案】ABC
【分析】
直线l恒过定点(2，-4)，画出图形，对k分类讨论并借助导数求出的取值范围即可作答.
【详解】
直线恒过定点A(2，-4)，
由点(0，0)到直线的距离得，即直线与圆相离，
(1)当l的斜率k满足|k|<1时，作出一条纵截距为负数的直线平行于l，如图：
要使得最小，P应位于切点处，作PC⊥x轴交直线l于点C，过Q作直线QB⊥PC于点B，
当Q位于点C的左方时，，当Q位于点C的右方时，同理也有，于是有，
设直线与圆相切，则有，即切线的纵截距，而直线l的纵截距为，
，在上递增，；
(2)当l的斜率k满足时，作出一条纵截距为负数的直线平行于l，如图：
要使得最小，P应位于切点处，作PC⊥y轴交直线l于点C，过Q作直线QB⊥PC于点B，
当Q位于点C的左方时，，当Q位于点C的右方时，同理也有，于是有，
设直线与圆相切，则有，即切线的横截距，而直线l的横截距为，
，在上递减，，
综上得，则选项ABC满足.
故选：ABC
44．已知抛物线方程为，直线，点为直线l上一动点，过点P作抛物线的两条切线，切点为A､B，则以下选项正确的是（ ）
A．当时，直线方程为B．直线过定点
C．中点轨迹为抛物线D．的面积的最小值为
【答案】ACD
【分析】
运用导数知识求出切线方程，可以得到直线的表达式，判断A、B选项；联立直线与抛物线的方程组，求解出其中点坐标，解出中点轨迹判断C选项；运用弦长公式和点到直线距离公式求出三角形的底和高，得到三角形面积表达式，求出最值判断D选项.
【详解】
解析：，，设，
则，即，
同理，都过点，
直线，即，
当时，.故A正确；
，，直线过定点，故B错误；
联立，消去得，，，
，中点坐标为，故其轨迹方程为，故C正确；
，，
，
当时，，故D正确；
故选：ACD
45．过抛物线：焦点的直线交于，两点，为坐标原点，则（ ）
A．不存在直线，使得
B．若，则直线的斜率为
C．过作准线的垂线，垂足为，若，则
D．过，两点分别作抛物线的切线，则两切线交点的纵坐标为定值
【答案】ACD
【分析】
设：，，，联立抛物线方程应用韦达定理求、、，利用向量数量积的坐标表示求可判断A的正误，由结合图象有，进而求，坐标即可确定直线的斜率判断B的正误，根据抛物线定义及余弦定理求判断C的正误，利用导数求切点处的切线方程，根据切线交点横坐标相等求纵坐标判断D的正误.
【详解】
由题设，设：，，，联立抛物线方程整理可得：，且，则，，.
∴由上知：，，则，故不存在直线，使得，A正确；
若，则，结合可得，，
∴，，故，B错误；
如上图示，若，由抛物线定义知：，
∴，即，可得，
在△中，，C正确；
由抛物线方程得，故过的切线为，过的切线为，令，整理得，
∴，两切线交点的纵坐标为定值，D正确.
故选：ACD
46．在中，，为的中点，且，则下列说法中正确的是（ ）
A．动点的轨迹是双曲线B．动点的轨迹关于点对称
C．是钝角三角形D．面积的最大值为
【答案】BD
【分析】
由联想到双曲线的定义，可以考虑以两点作为焦点，为原点作图，设=，此时点在以为圆心，为半径的圆上，由，知点在双曲线上，由图逐项判断即可．
【详解】
以为原点，为轴建立直角坐标系．
设=，此时点在以为圆心，为半径的动圆上．
由，知点在以为焦点，的双曲线上且．
对点有，，从而，当时，最大，故，，故正确；
时，得到另一个点，此时为直角三角形，故错误；
∵非定值，∴不以双曲线为轨迹，故错误；
∵，∴一定有关于的对称点关于原点对称，故正确．
故选：BD．
47．已知抛物线，点，过M作抛物线的两条切线，其中A，B为切点，直线与y轴交于点P，则下列结论正确的有（ ）
A．点P的坐标为B．
C．的面积的最大值为D．的取值范围是
【答案】AC
【分析】
由，可得，得到点处的切线的斜率分别为和，设过点的切线方程为，联立方程组，由由，求得，根据，可判断B不正确；由，得出的直线方程为，将代入直线的方程，可判定A正确；设直线的方程为，根据点到直线的距离公式和弦长公式，求得，可判定C正确；由，结合韦达定理，得到，得出不等式组，可判定D不正确.
【详解】
由题意，设，由，可得，
所以点处的切线的斜率为，点处的切线的斜率为，
设过点的切线方程为，
联立方程组，可得，
由，可得，
又由，则，
所以不垂直，所以B不正确；
由，所以的直线方程为，
即，将代入直线的方程，可得，
由知，方程成立，所以点在直线上，所以A正确；
由点在直线上，可设直线的方程为，
则点到的距离为，
且
，
所以，
因为，可得，所以的最大值为，所以C正确；
由，所以，
由，可得，
所以，因为，可得，
又由，设，可得，
即，解得或，
即的取值范围是，所以D不正确.
故选：AC.
48．已知抛物线E：的焦点为F，准线l交x轴于点C，直线m过C且交E于不同的A，B两点，B在线段上，点P为A在l上的射影．下列命题正确的是（ ）
A．若，则B．若P，B，F三点共线，则
C．若，则D．对于任意直线m，都有
【答案】BCD
【分析】
解法一：设出直线方程，然后与抛物线方程联立，结合韦达定理与抛物线的定义进而逐项分析即可，其中D选项需要结合均值不等式；解法二：对A选项首先假设，然后推出矛盾即可判断，B，C，D选项则同解法一一样.
【详解】
解法一：由已知条件可得
由抛物线的对称性，不妨设直线的方程为
依题意，由整理，得
当，即时，由韦达定理，
得.
对于选项，因为直线的斜率为，
所以，即
又，所以，解得，所以
所以，
故，故错误；
对于选项，易得，所以
当三点共线时，，
所以
由和，解得，
所以故正确
对于选项，过作，垂足为由已知可得，
所以.
又，所以.
由抛物线的定义，得
因此故正确；
对于选项，因为，
所以，又，
故成立.故正确.
故选：BCD.
解法二：对于选项，假设成立，则为等腰直角三角形，
，所以为等腰直角三角形，则点在轴上，这与已知条件显然矛盾，故
故错误，其他选项同解法一进行判断.
故选：BCD.
49．在平面直角坐标系中，已知抛物线，过点作与轴垂直的直线，与抛物线交于、两点，则下列说法正确的是（ ）
A．若，则
B．若为正三角形，则
C．若抛物线上存在两个不同的点、（异于、），使得，则
D．当取得最大值时，
【答案】BCD
【分析】
由求出的取值范围，可判断A选项的正误；求出、，根据解出，可判断B选项的正误；设点，由得出关于的方程有四个不同的实根，求出的取值范围，可判断C选项的正误；设，求得的最大值及其对应的的值以及的值，可判断D选项的正误.
【详解】
对于A选项，将代入抛物线的方程可得出，则，
所以，，，由可得，解得，A选项错误；
对于B选项，设点，则点，则，，
由于为正三角形，则，即，解得，B选项正确；
对于C选项，在抛物线上任取一点，则，
由，可得，整理可得，
即，即，
关于的方程有四个不同的实根，则，解得，C选项正确；
对于D，设，，
其中为锐角，且，，
当且仅当时，取得最大值，
则，，
则，即，解得，D选项正确.
故选：BCD.
50．已知椭圆上有一点P，分别为左､右焦点，的面积为S，则下列选项正确的是（ ）
A．若，则B．若，则
C．若为钝角三角形，则D．椭圆C内接矩形的周长范围是
【答案】ACD
【分析】
用椭圆的焦点三角形和内接矩形等知识分别对四个选项判断即可.
【详解】
对于椭圆，设，，，则
，由此可得…①，
所以的面积.
对于选项A：若，则，故A正确；
对于选项B：由①知（当且仅当即点是短轴端点时取等号），所以，因此不可能是，故B错误；
对于选项C：由以上分析可知，不可能是钝角，由对称性不妨设是钝角.先考虑临界情况，当时，易得，此时，结合图形可知，当是钝角时，故C正确；
对于选项D：令，，
则椭圆内接矩形的周长为，其中锐角满足，.
由得，所以，周长的范围是，即，故D正确.
故选：ACD.
51．设，是抛物线：上两个不同的点，为坐标原点，若直线与的斜率之积为-4，则下列结论正确的有（ ）
A．B．
C．直线过抛物线的焦点D．面积的最小值是2
【答案】ACD
【分析】
对于选项B，可以通过特殊点来判断，而对于选项ACD，可以通过设直线，再联立方程组，结合韦达定理一一判断即可.
【详解】
取，，满足，从而，故B错误；
由题意可知直线的斜率不为0，设直线的方程为，，，
联立，整理得，则，.
因为，所以，所以直线的方程为，
则直线过点，故C正确；
因为抛物线的焦点为，所以直线过焦点，
则由抛物线的性质可知，故A正确；
由上可得直线的方程为，则，
原点到直线的距离，
则，故D正确.
故选：ACD.
52．已知双曲线的左焦点为，为右支上的动点，过作的一条渐近线的垂线，垂足为，为坐标原点，当最小时，，，成等差数列，则下列说法正确的是（ ）
A．若的虚轴长为2，则到的一条渐近线的距离为2
B．的离心率为
C．若的焦距为2，则到的两条渐近线的距离之积小于
D．若的焦距为10，当最小时，则的周长为
【答案】BCD
【分析】
设出双曲线的右焦点，根据双曲线的定义以及题意得到，，对A，写出双曲线的一条渐近线方程利用点到直线的距离即可求解；对B，根据离心率的公式即可求解；对C，根据双曲线的焦距以及离心率，求出双曲线的方程，设出点的坐标，表示出到的两条渐近线的距离，再根据点在双曲线上即可求解，对D，根据题意可得，在中利用余弦定理求出，即可求解.
【详解】
解：设双曲线的右焦点为，
则，
，
故当最小时，即取得最小值，
故当三点共线时最小，
设双曲线的一条渐近线为：，
故，
即，
，
又，，成等差数列，
故,
即，
即，
又，
将代入得：.
对A，若的虚轴长为2，则，
设双曲线的一条渐近线为：，
则到的一条渐近线的距离为，故A错误；
对B，由上述可知：，
即，
即，故B正确；
对C，若的焦距为2，则，
由得：，
故双曲线的方程为：，
双曲线的渐近线方程为：，
即，
设，
则到两条渐近线的距离分别为：
，
，
又在双曲线上，
故，
即，
到两条渐近线的距离之积为：，
故C正确；
对D，若的焦距为10，则，
由得：，
则的周长为：，
又，
，
在中，由余弦定理得：,
即，
故，
故，故D正确.
故选：BCD.
53．双扭线最早于1694年被瑞士数学家雅各布·伯努利用来描述他所发现的曲线．在平面直角坐标系xOy中，把到定点，距离之积等于的点的轨迹称为双扭线C．已知点是双扭线C上一点，下列说法中正确的有（ ）
A．双扭线C关于原点O中心对称；
B．；
C．双扭线C上满足的点P有两个；
D．的最大值为．
【答案】ABD
【分析】
对A，设动点，则对称点代入轨迹方程，显然成立；对B，根据的面积范围证明；对C，若，则在y轴上，代入轨迹方程求解；对D，根据余弦定理分析中的边长关系，进而利用三角形的关系证明即可.
【详解】
对A，设动点，由题意可得的轨迹方程为
把关于原点对称的点代入轨迹方程，显然成立；
对B，因为，故．
又，所以，
即，故．故B正确；
对C，若，则在的中垂线即y轴上．
故此时，代入，
可得，即，仅有一个，故C错误；
对D，因为，
故，
，
因为，，
故．
即，
所以．
又，当且仅当，，共线时取等号．
故，
即，解得，故D正确．
故选：ABD.
54．已知抛物线的焦点为，过点的直线交抛物线于、两点，以线段为直径的圆交轴于、两点，设线段的中点为，则（ ）
A．
B．若，则直线的斜率为
C．若抛物线上存在一点到焦点的距离等于，则抛物线的方程为
D．若点到抛物线准线的距离为，则的最小值为
【答案】AD
【分析】
设点、，设直线的方程为，将直线的方程与抛物线的方程联立，列出韦达定理，利用平面向量数量积的坐标运算可判断A选项的正误，根据求出的值，可判断B选项的正误，利用抛物线的定义求出的值，可判断C选项的正误，求出的取值范围，可判断D选项的正误.
【详解】
若直线轴，则直线与抛物线有且只有一个交点，不合乎题意.
设点、，设直线的方程为，
联立，整理可得，，
由韦达定理可得，，，
，A正确；
，解得，
所以，直线的斜率为，B错误；
抛物线上一点到焦点的距离为，则，可得，
故抛物线方程：，C错误；
抛物线的焦点到准线的距离为，则，所以，抛物线的方程为，
所以，，，，
所以，圆的直径为，则，
点到轴的距离为,
，
，，，
即，D正确.
故选：AD.
55．已知四面体的所有棱长均为，则下列结论正确的是（ ）
A．异面直线与所成角为
B．点到平面的距离为
C．四面体的外接球体积为
D．动点在平面上，且与所成角为，则点的轨迹是椭圆
【答案】BC
【分析】
在正四面体中通过线面垂直可证得，通过计算可验证BC,通过轨迹法可求得的轨迹为双曲线方程即可得D错误.
【详解】
取中点,连接,可得面,则,故A错误；
在四面体中，过点作面于点,则为为底面正三角形的重心，因为所有棱长均为,,即点到平面的距离为,故B正确；
设为正四面体的中心则为内切球的半径，我外接球的半径，
因为，所以，即,
所以四面体的外接球体积,故C正确；
建系如图：,设，则
因为，所以，
即，平方化简可得：，可知点的轨迹为双曲线,故D错误.
故选：BC．

56．在平面直角坐标系中，动点与两个定点和连线的斜率之积等于，记点的轨迹为曲线，直线：与交于，两点，则（ ）
A．的方程为B．的离心率为
C．的渐近线与圆相切D．满足的直线有2条
【答案】CD
【分析】
由已知结合斜率的两点式有，即可得的方程为，进而可求的离心率，利用圆心到的渐近线距离判断圆与的渐近线的位置关系，联立直线与曲线，结合求值的个数，由此即可判断各选项的正误.
【详解】
令，由题意得：，即得，
∴A错误，又，即，故B错误，
由E的渐近线为，而圆心为，半径为1，
∴到距离为，故的渐近线与圆相切，故C正确，
联立曲线E与直线的方程，整理得：，，
∴，而，
代入整理：，即有或(由与无交点，舍去)，故，
∴D正确.
故选：CD
57．在棱长为1的正方体中，已知点P为侧面上的一动点，则下列结论正确的是（ ）
A．若点P总保持，则动点P的轨迹是一条线段；
B．若点P到点A的距离为，则动点P的轨迹是一段圆弧；
C．若P到直线与直线的距离相等，则动点P的轨迹是一段抛物线；
D．若P到直线与直线的距离比为，则动点P的轨迹是一段双曲线.
【答案】ABD
【分析】
由平面且平面平面，即可判断A；根据球的性质及与正方体的截面性质即可判断B；作，，连接，作.建立空间直角坐标系，由即可求得动点P的轨迹方程，即可判断C；根据题意，由距离比即可求得轨迹方程，进而判断D.
【详解】
对于A，，且，所以平面，平面平面，故动点P的轨迹为线段，所以A正确；
对于B，点P的轨迹为以A为球心、半径为的球面与面的交线，即为一段圆弧，所以B正确；
对于C，作，，连接；作.由，在面内，以C为原点、以直线、、为x，y，z轴建立平面直角坐标系，如下图所示：
设，则，化简得，P点轨迹所在曲线是一段双曲线，所以C错误.
对于D，由题意可知点P到点的距离与点P到直线的距离之比为，结合C中所建立空间直角坐标系，可得，所以，代入可得，化简可得，故点P的轨迹为双曲线，所以D正确.
综上可知，正确的为ABD.
故选：ABD.
58．已知抛物线：的焦点到准线的距离为2，过点的直线与抛物线交于，两点，为线段的中点，为坐标原点，则下列结论正确的是（ ）
A．的准线方程为B．线段的长度最小为4
C．的坐标可能为D．恒成立
【答案】BCD
【分析】
根据抛物线的几何意义判定，联立直线与抛物线方程结合韦达定理计算即可得解.
【详解】
焦点到准线的距离即为，所以抛物线的焦点为，准线方程为，A项错误.
当垂直于轴时长度最小， 此时，，所以，B项正确.
设，，直线的方程为.联立，消去可得，消去可得，所以，，当时，可得，所以C正确，又，，所以，所以D正确.
故选：BCD
59．已知，，记，则
A．的最小值为B．当最小时，
C．的最小值为D．当最小时，
【答案】BC
【分析】
将所求最小值转化为为函数图象上的点到直线上的点的距离的最小值的平方；利用导数可求得与直线平行的函数的切线，由此可求得切点坐标，则切点到直线距离的平方即为所求最小值，利用点到直线距离公式求得最小值；求得过切点且与垂直的直线方程，两直线方程联立即可求得最小时，的值.
【详解】
由得：
的最小值可转化为函数图象上的点到直线上的点的距离的最小值的平方
由得：
与直线平行的直线的斜率为
则令，解得： 切点坐标为
到直线的距离
即函数上的点到直线上的点的距离的最小值为
的最小值为
过与垂直的直线为
即
由，解得：，即当最小时，
故选：
60．已知双曲线的左、右焦点分别为，P为双曲线上一点，且，若，则下面有关结论正确的是（ ）
A．B．C．D．
【答案】ABCD
【分析】
根据对分类讨论，利用双曲线的定义以及，再结合对应的余弦定理，即可计算出离心率的值，从而可求的关系.
【详解】
若为锐角时，，如图所示，
因为，，所以，
所以，
所以，所以，所以，
所以，，故BD正确；
若为钝角时，，如图所示，
因为，，所以，
所以，
所以，所以，所以，
所以，，故AC正确.
故选：ABCD.
61．已知到两定点，距离乘积为常数16的动点的轨迹为，则（ ）
A．一定经过原点B．关于轴、轴对称
C．的面积的最大值为45D．在一个面积为64的矩形内
【答案】BCD
【分析】
先由已知条件求出点的轨迹方程，然后结合轨迹方程及三角形的面积公式逐一判断即可得解.
【详解】
解：设点的坐标为，由题意可得.
对于A，将原点坐标代入方程得，所以，A错误；
对于B，点关于轴、轴的对称点分别为、，
∵，
∵，
则点、都在曲线上，所以，曲线关于轴、轴对称，B正确；
对于C，设，，，则，
由余弦定理得，
当且仅当时等号成立，则，所以，
则的面积为，C正确；
对于D，，
可得，得，解得，
由C知，，得，
曲线在一个面积为的矩形内，D正确.
故选：BCD.
62．已知分别是双曲线的左、右焦点，A为左顶点，P为双曲线右支上一点，若且的最小内角为，则（ ）
A．双曲线的离心率B．双曲线的渐近线方程为
C．D．直线与双曲线有两个公共点
【答案】ABD
【分析】
A．根据以及对应的余弦定理计算出离心率的值；B．根据离心率的值，计算出的值，即可求解出双曲线的渐近线方程；C．根据的大小关系判断出三角形的形状，再根据长度关系判断是否成立；D．联立直线与双曲线，利用一元二次方程的，判断出直线与双曲线的交点个数.
【详解】
A．因为，，所以，，
又因为，所以，
所以，所以，所以，故结论正确；
B．，所以，所以，所以渐近线方程为，故结论正确；
C．因为，所以，所以，
又因为，所以，所以，所以结论不成立；
D．因为，所以，所以，
所以，
所以直线与双曲线有两个公共点，所以结论正确.
故选：ABD.
63．过抛物线的焦点作直线交抛物线于，两点，为线段的中点，则（ ）
A．以线段为直径的圆与直线相离B．以线段为直径的圆与轴相切
C．当时，D．的最小值为4
【答案】ACD
【分析】
根据抛物线的定义和直线与圆的相切关系对四个选项逐一判断即可.
【详解】
对于选项A，点到准线的距离为，于是以线段为直径的圆与直线一定相切，进而与直线一定相离：
对于选项B，显然中点的横坐标与不一定相等，因此命题错误.
对于选项C，D，设，，直线方程为，联立直线与抛物线方程可得 ，，，若设，则，于是，最小值为4；当可得，
，所，.
故选:ACD.
64．已知抛物线的焦点为，直线的斜率为且经过点，直线与抛物线交于点、两点（点在第一象限），与抛物线的准线交于点，若，则以下结论正确的是
A．B．C．D．
【答案】ABC
【分析】
作出图形，利用抛物线的定义、相似三角形等知识来判断各选项命题的正误.
【详解】
如下图所示：
分别过点、作抛物线的准线的垂线，垂足分别为点、.
抛物线的准线交轴于点，则，由于直线的斜率为，其倾斜角为，
轴，，由抛物线的定义可知，，则为等边三角形，
，则，，得，
A选项正确；
，又，为的中点，则，B选项正确；
，，（抛物线定义），C选项正确；
，，D选项错误.
故选：ABC.
65．已知点F是抛物线的焦点，AB,CD是经过点F的弦且AB⊥CD，AB的斜率为k，且k>0，C,A两点在x轴上方.则下列结论中一定成立的是（ ）
A．B．四边形ACBD面积最小值为
C．D．若，则直线CD的斜率为
【答案】ACD
【分析】
利用抛物线的极坐标方程求出，然后即可计算求解，判断出各选项的真假．
【详解】
设AB的倾斜角为，则有，所以，C正确；
，若，则，，
直线CD的斜率为，D正确；
，所以B不正确；
设 ，由抛物线过焦点弦的性质可知，，
，所以A正确．
故选：ACD．
66．过点作圆C：的两条切线，切点分别为A，B，则下列说法正确的是（ ）
A．
B．所在直线的方程为
C．四边形的外接圆方程为
D．的面积为
【答案】BCD
【分析】
在中利用等面积法得到，即可求出的长度，进而可得，即可判断A选项；求出以为圆心，为半径的圆的方程与圆C做差，即可得到所在直线的方程，进而判断B选项；根据平面几何知识可得四边形的外接圆是以为直径的圆，进而可以求出圆的方程进行判断；求出的长度，利用面积公式即可求出的面积，从而可判断D选项.
【详解】
因为，所以以为圆心，为半径的圆交圆于两点，
因为,
又因为以为圆心，为半径的圆为，
与相减得
所以所在直线的方程为，故B正确；
连接交于，等面积法可得，即，所以，即，所以，故A错误；
四边形的外接圆是以为直径的圆，故圆心为，半径为的圆，故方程为，即，故C正确；
因为，
所以，故D正确；
故选：BCD.
67．已知点为椭圆（）的左焦点，过原点的直线交椭圆于，两点，点是椭圆上异于，的一点，直线，分别为，，椭圆的离心率为，若，，则（ ）
A．B．C．D．
【答案】AC
【分析】
设出右焦点，根据椭圆定义结合对称性以及余弦定理可求得的关系，则离心率可求；设出的坐标，根据对称性写出的坐标，利用点差法可求得的表示，结合的关系可求解出的值.
【详解】
设椭圆的右焦点，
连接，，根据椭圆对称性可知四边形为平行四边形，
则，且由，可得，
所以，则，．
由余弦定理可得，
所以，所以椭圆的离心率．
设，，则，，，
所以，又，，相减可得．
因为，所以，所以．
故选：AC．
68．已知点在椭圆上，过点分别作斜率为-2，2的直线，与直线，分别交于，两点.若，则实数的取值可能为（ ）
A．B．1C．2D．3
【答案】CD
【分析】
设出，，三点的坐标→利用四边形为平行四边形构造方程→将转化为关于点坐标的关系式→的最大值→的范围.
【详解】
设，，，则，，
由题得四边形为平行四边形，所以，
故故.
因为，所以，
故实数的取值范围为，
故选:CD.
69．曲率半径是用来描述曲线上某点处曲线弯曲变化程度的量，已知对于曲线上点处的曲率半径公式为，则下列说法正确的是（ ）
A．对于半径为的圆，其圆上任一点的曲率半径均为
B．椭圆上一点处的曲率半径的最大值为
C．椭圆上一点处的曲率半径的最小值为
D．对于椭圆上点处的曲率半径随着的增大而减小
【答案】AC
【分析】
利用曲率半径公式的定义，A中有圆上任一点；B、C中由椭圆在， 处分别是最大、最小处，结合公式求得曲率半径的范围；D中由公式得，构造，利用导数研究其单调性即可，进而可确定正确选项.
【详解】
A：由题设知：圆的方程可写为，所以圆上任一点曲率半径为，正确；
B、C：由弯曲最大处为，最小处为，所以在处有，
在处有，即，故B错误，C正确；
D：由题意，处的曲率半径，而，
所以，令，
则在上有恒成立，故在上随着的增大而增大，错误；
故选：AC.
70．如图，已知椭圆的左､右顶点分别是，上顶点为，在椭圆上任取一点，连结交直线于点，连结交于点(是坐标原点)，则下列结论正确的是（ ）
A．为定值B．
C．D．的最大值为
【答案】ABC
【分析】
设点的坐标为，，而，从而可求出直线的斜率，进而可得直线的方程，令，求出的值，可得点的坐标，然后可求出的斜率，进而可对选项A，B，C进行判断，求出直线，的方程，两方程联立可求出点的坐标，从而可表示出的长，进而可判断其最值
【详解】
解：椭圆的左右顶点分别，
因为点在椭圆上，所以设点的坐标为，，
对于A，，所以A正确；
对于B，因为，
所以直线为，令，得，所以点的坐标为，所以，所以，所以B正确；
对于C，因为，所以，所以，所以C正确；
对于D，直线为，直线为，
由两直线的方程联立方程组，解得，
所以点的坐标为，
因为，
所以
当时，
所以的最大值为错误，
故选：ABC
第II卷（非选择题）
三、填空题
71．已知，是双曲线的左、右焦点，A，B分别在双曲线的左右两支上，且满足（为常数），点C在x轴上，，，则双曲线的离心率为_______．
【答案】
【分析】
根据平行线的性质，结合角平分线的性质、双曲线的定义、余弦定理、双曲线离心率公式进行求解即可.
【详解】
解析： ，∵，所以∴，∴，设，则．由可知，平分，由角分线定理可知，∴，∴，，，由双曲线的定义知，，∴，即①，，∴，∴，即是等边三角形，∴，在中，由余弦定理知，，即，化简得，②，由①②可得，，∴离心率．
故答案为：
72．已知平面向量、、满足，，，则的取值范围为______．
【答案】
【分析】
设，，，作，，，则，求出线段的中点的轨迹方程为，可得出，设点，由结合向量模的三角不等式可求得的取值范围.
【详解】
如图，设，，，作，，，则，
则，，，
令，即，
，
整理得，
故点的轨迹方程为，，
设点，圆的方程为，半径为，
因为，且，，
所以，，.
即，即.
故的取值范围是.
故答案为：.
73．已知平面非零向量、，、满足，，若，，则的最小值为______．
【答案】
【分析】
设，，，，分析可知点、在抛物线上，且为抛物线的一条过焦点的弦，并可得出以为直径的圆与抛物线准线相切，可得值点的轨迹为圆，数形结合可得出的最小值.
【详解】
设，，，则，，
设点、，则，
设，则，则，，
由可得，化简可得，
故点、在抛物线上，
因为，则，故、、三点共线，
即为抛物线的一条过焦点的弦，
设，则，，所以，，
故点的轨迹是以为直径的圆，
设点、，则，
而是线段的中点到抛物线准线的距离，
故以为直径的圆与抛物线准线相切，
当点不是圆与直线的切点时，；
当点是圆与直线的切点时，.
综上所述，的最小值为.
故答案为：.
74．设,分别是椭圆的左､右焦点，过点的直线交椭圆于两点，，若，则椭圆的离心率为___________.
【答案】
【分析】
求椭圆的离心率，要列出关于的等量关系式，设，根据椭圆的定义以及，可以表示出三角形各边的长度，通过余弦定理得到各边关于的表达式，根据几何关系可以列出关于的等量关系式，从而求出离心率
【详解】
设，则，，
，.
，
在中，由余弦定理得，，
，
化简可得，而，故，
，，
，
，
是等腰直角三角形，
，
椭圆的离心率 ，
故答案为：.
75．已知双曲线的左、右焦点分別为，过作直线l垂直于双曲线的一条渐近线，直线l与双曲线的两条渐近线分别交于A，B两点，若，且，则双曲线C的离心率的取值范围为________．
【答案】
【分析】
由题意知：在、之间，若过作直线l垂直于B，交于A，可令求、坐标，进而可得、，应用向量共线的坐标表示，列方程得到a、c的齐次方程，即可求的范围.
【详解】
由题意，双曲线C的渐近线为，若过作直线l垂直于B，交于A，.
∵且，
∴在、之间，如上图示，令，
∴，，则，，
∴， 即，
∴，故，得，又，
∴.
故答案为：
76．已知椭圆C：的左，右焦点分别是是椭圆C上第一象限内的一点，且的周长为.过点作的切线，分别与轴和轴交于两点，为原点，当点在上移动时，面积的最小值为___________.
【答案】2
【分析】
设出直线的方程，根据焦点三角形的周长求解出的值，则椭圆方程可求，联立椭圆方程与抛物线方程并根据相切关系对应的求解出的关系式，然后表示出面积并结合基本不等式求解出面积的最小值.
【详解】
设直线方程为，
因为的周长为，所以，且，
所以，所以椭圆，
联立可得，
所以，所以，
又因为与坐标轴交于，
所以，
取等号时，
所以面积的最小值为，
故答案为：.
77．已知抛物线上一点，且抛物线上两个动点满足，若直线过定点，则的坐标为 _________.
【答案】
【分析】
根据题意设出合适直线的方程，联立直线与抛物线的方程，得到关于的一元二次方程及其韦达定理形式，将转化为和韦达定理有关的形式，由此求解出的关系式，用表示后即可求得所过的定点坐标.
【详解】
由题意可知，直线的斜率不为零，所以设，，
所以，所以，所以，
又因为，所以，
所以，所以，所以，
所以，所以过定点，
故答案为：
78．已知点在抛物线上，过点作抛物线的切线与轴交于点，抛物线的焦点为，若，则的坐标为___________.
【答案】
【分析】
设出点坐标，求得切线方程，由此求得点坐标，根据列方程，解方程求得点的坐标.
【详解】
，
设，，
依题意可知过点的切线斜率存在且不为，设为，
则切线方程为，
即，
由，
化简得，
，，
，，
故切线方程为，
令得，故，
，，
依题意，，
即，
，，由于，
故，此时，
所以点坐标为.
故答案为：
79．已知抛物线的焦点到其准线的距离为4，圆，过的直线与抛物线和圆从上到下依次交于四点，则的最小值为_________.
【答案】
【分析】
根据已知条件先求出抛物线的方程，然后将问题转化为计算“”的最小值，通过抛物线的焦半径公式将表示为坐标的形式，采用直线与抛物线联立的思想，根据韦达定理和基本不等式求解出最小值.
【详解】
因为抛物线的焦点到准线的距离为，所以，所以抛物线方程为，
如下图，，
因为，
设，所以，
所以，
设，所以，，所以，
所以，取等号时，
所以的最小值为，
故答案为：.

80．过抛物线：的焦点作直线，分别与抛物线交于，和，，若直线，的斜率分别为，，且满足，则的最小值为___________.
【答案】12
【分析】
根据抛物线弦长公式，结合基本不等式进行求解即可.
【详解】
抛物线的焦点坐标为，设直线的方程为，
与抛物线方程联立得：，
设，所以，
同理可得：，，
所以有：
，
因为，当且仅当时，等号成立，所以，
故答案为：12
81．双曲线的渐近线为正方形的边、所在的直线，点为该双曲线的右焦点，若过点的直线与直线、的分别相交于、两点，则内切圆半径的最大值为______．
【答案】
【分析】
根据双曲线和正方形的对称性、三角形的面积公式，结合基本不等式、直角三角形内切圆半径公式、分式型函数的单调性进行求解即可.
【详解】
由题意得，过、向轴作垂线，垂足分别为，．
设，，则，．
，所以有．
又，有．（当且仅当时等号成立）．
的内切圆半径令，，则在上单调递减．
∴当时，有最大值为．
故答案为：
82．已知双曲线，，，是坐标原点，过点的直线交双曲线于，两点，若直线上存在点满足，则的最小值是___________.
【答案】6
【分析】
设OA的中点为N,根据已知条件，利用向量的加法的模的几何意义可得N到直线l的距离小于等于2.当直线l与双曲线的左右支各交于一个交点时，根据双曲线的几何性质即可得到|MN|的最小值为2a=6,接下来验证在当直线l与双曲线的右支交于两点时，且在N到直线l的距离小于等于2时，|MN|的长度大于6即可.
【详解】
设OA的中点为N,则N的坐标为.
由已知可得直线l上存在点P,使得
即使得，即N到直线l的距离小于等于2.
当直线l与双曲线的左右支各交于一个交点时，由双曲线的几何性质可得弦长|MN|的最小值为2a=6,此时直线l即为x轴，N到l的距离为0，符合题意.
当直线l与双曲线的右支交于两点时，弦越短，直线的斜率的绝对值越大，
当斜率不存在时，即MN为通径时，|MN|的长度取得最小值但此时点M到直线l的距离为,
当直线的斜率存在时，直线的斜率的取值范围,直线的方程为,.
由N到直线l的距离小于等于2，即：，解得，
∴,直线的方程为代入双曲线的方程并整理化简得：,
,
易得,设M,N的横坐标分别为,则,
,
,∴
综上所述，|MN|的最小值为6，
故答案为：6.
83．已知、分别为抛物线与圆上的动点，抛物线的焦点为，、为平面内两点，且当取得最小值时，点与点重合；当取得最大值时，点与点重合，则的面积为______.
【答案】
【分析】
利用抛物线和圆的几何性质找出点、，并求出点、的坐标，求出以及点到直线的距离，利用三角形的面积公式可求得的面积.
【详解】
抛物线的焦点为，圆的标准方程为，圆心为，半径为，如下图所示：
抛物线的准线为，过点作抛物线的垂线，垂足为点，
由抛物线的定义可得，则，
当时，取最小值，此时取最小值，
直线的方程为，联立，解得，即点，
点到圆上任意一点的距离，当且仅当为射线与圆的交点，且为线段上的点，
所以，，
当且仅当为射线与抛物线的交点，且为射线与圆的交点（为线段上的点），取得最大值.
直线的斜率为，直线的方程为，
联立，解得，即点，
直线的斜率为，直线的方程为，
即，，
点到直线的距离为，因此，.
故答案为：.
84．已知，分别为双曲线（，）的左、右焦点，过点作圆的切线交双曲线左支于点，且，则该双曲线的渐近线方程为__________．
【答案】．
【分析】
设切点为，过作，垂足为，根据三角形中位线定理，结合正弦函数的定义，双曲线的定义、双曲线的渐近线方程进行求解即可.
【详解】
解：设切点为，过作，垂足为，
由题意可得，，，
由为的中位线，可得，
，
又，可得，，
，
又，
所以，
所以双曲线的渐近线方程为．
故答案为：．
85．已知二元函数的最小值为，则正实数a的值为________．
【答案】.
【分析】
根据两点间距离公式，可得的表达式的几何意义为：点与点的距离之和，作出图形，根据两点间线段最短，可得的距离即为最小值，化简计算，即可得结果.
【详解】
由题意得，
其几何意义为：点与点的距离之和，如图所示：
设点，则求的最小值即可，
以B为旋转中心，将绕点B顺时针旋转至，连接，
则均为等边三角形，
所以，
所以，取等号时四点共线，
即，
又，所以，
化简可得，
左右同时平方，根据，解得，
故答案为：2.
86．已知点，点为抛物线：的焦点，第一象限内的点在抛物线上，则的最大值为______．
【答案】．
【分析】
根据抛物线定义，结合换元法、基本不等式进行求解即可.
【详解】
由已知得，所以抛物线的方程为，准线：．
如图，过作于点，则由抛物线的定义可知，则．
设，在中，．
又，所以．记 ，则，
所以，
由基本不等式可得（当且仅当时等号成立）.
所以，即的最大值为．
故答案为：
87．已知：，，，，则最小值为________.
【答案】
【分析】
由题意不妨设，，在直角坐标系中根据向量的加减法可得，利用数形结合求解即可.
【详解】
∵，，
不妨设，，
在直角坐标系中作出，，如图，
，记，则点在过原点与直线平行的直线上，
易知直线方程是即，
记，则，
∴在以为圆心，半径为的圆上，
到直线的距离为，
∴的最小值为.
即最小值为.
故答案为：.
88．圆的方程为，圆的方程为，过圆上任意一点作圆的两条切线、，切点分别为、，则的最小值为__________.
【答案】
【分析】
设，可得出，利用三角函数的定义以及平面向量数量积的定义可得出，利用圆的几何性质求得的取值范围，结合双勾函数的单调性可求得的最小值.
【详解】
设，则，
由切线长定理可得，，，
，
圆心的坐标为，则，
由图可得，即，则，
由双勾函数的单调性可知，函数在区间上单调递增，
所以，当时，取得最小值.
故答案为：.
89．已知椭圆的左、右焦点分别为、，过椭圆的右焦点作一条直线交椭圆于点、.则内切圆面积的最大值是_________.
【答案】
【详解】
令直线：，与椭圆方程联立消去得，可设，则，．可知，又，故．三角形周长与三角形内切圆的半径的积是三角形面积的二倍，则内切圆半径，其面积最大值为．故本题应填．
90．如图所示，是椭圆的短轴端点，点在椭圆上运动，且点不与重合，点满足，则＝____________．
【答案】2
【分析】
本题首先可以设出点坐标，然后利用椭圆的相关性质得出直线的斜率，再通过得出直线的斜率以及直线的方程，然后使用同样的方式得出直线的方程，并对两方程进行联立化简，最后再利用点在椭圆上得出与的关系，最后得出结果．
【详解】
设，则直线的斜率为，
由所以直线的斜率为的斜率为，
于是直线的方程为，
同理，直线的方程为，
联立两直线方程，消去，得，
因为在椭圆上，所以，
从而，所以，
所以故选A．
91．在平面直角坐标系中，已知直线上存在点，过点作圆的切线，切点分别为，，且，则实数的取值范围为________．
【答案】
【分析】
作出图形，取的中点，可得点，根据已知条件计算得出，，由此可得出坐标原点到直线的距离，可得出关于的不等式，由此可解得实数的取值范围.
【详解】
取的中点，如图，
由圆的几何性质可得，且，
则，所以，
由，
所以，
由，，.
所以，则，点到直线的距离为，
则或，所以，
故答案为：．
92．已知中，角，，所对的边分别是，且，则的面积的最大值是___________．
【答案】
【分析】
设，则点，，设，根据题意可求出点在以为圆心，为半径的圆上，则构造基本不等式可得结果.
【详解】
如图建立坐标系，设，则点，，设，
则由得，
化简可得：，
这说明点在以为圆心，为半径的圆上（不含轴上两点），
于是，

（当且仅当，，取到等号）．
93．已知为双曲线：上一点，为坐标原点，，为曲线左右焦点.若，且满足，则双曲线的离心率为___.
【答案】
【分析】
由知为外接圆的圆心，即有，运用勾股定理和双曲线的定义，化简整理，结合离心率公式计算即可得到.
【详解】
，
为外接圆的圆心，
，
又，
，
由双曲线定义可知，
解得，
由
即
即有
所以
故答案为：
94．已知抛物线，其焦点为，准线为，过焦点的直线交抛物线于点、（其中在轴上方），，两点在抛物线的准线上的投影分别为，，若，，则____________.
【答案】3
【分析】
根据抛物线的的定义可得，利用直角三角形可求出，由面积等积法求出，求出直线的倾斜角，利用公式，计算.
【详解】
由抛物线的定义得：，，易证，
∴，
∴
∵，
∴，
.∴，
∵，
∴为等边三角形.
∴直线的倾斜角.
∴，.
∴.
故答案为：3
95．已知双曲线（）的左、右焦点分别是、，为双曲线左支上任意一点，当最大值为时，该双曲线的离心率的取值范围是__________.
【答案】
【分析】
，，分，两种情况讨论，要注意题目中隐含的条件.
【详解】
由已知，，因为，当时，
，当且仅当时，取最大值，
由，所以；当时，的最大值小于，所以不合题意.
因为，所以，所以，所以
故答案为：
96．已知函数，则的最大值为______.
【答案】
【分析】
将该函数转化为两点连线的斜率问题，其中为定点，为单位圆上的动点，则可利用直线与圆的位置关系，解决本题.
【详解】
，
表示点和点连线的斜率，
又，
则点在单位圆上
设过点的直线的方程为：，
即，
故单位圆与该直线相切或相交，
，解得，
即，则
故答案为：.
97．已知和为抛物线的焦点和准线，点为上一点，过作于，若四点共圆（为原点)，则该圆的半径为____________.
【答案】
【分析】
作出函数图象,由四点共圆可知,圆心为垂直平分线的交点,由已知可求得直线的方程,由为中点,可求得点横坐标代入抛物线方程即可求得点坐标,进而知道点坐标,求出的垂直平分线方程和直线联立即可求得圆心坐标,进而求得结果.
【详解】
四点共圆，所以圆心在和的垂直平分线上，
设和的垂直平分线为，由知，
即点的横坐标为，又知点的横坐标为，
所以点横坐标为2代入抛物线易得（设在第一象限），
则，则知线段的垂直平分线方程为，
将与直线联立得圆心，所以圆的半径.
故答案为: .
98．在平面直角坐标系中，已知在圆：上运动，且.若直线：上的任意一点都满足，则实数的取值范围是__________.
【答案】
【分析】
先求出，再化简得，再代点到直线的距离公式解不等式得解.
【详解】
由题得圆的圆心.且,,
（其中是的夹角），
，
因为，
所以,
所以，
所以，
所以.
所以.
故答案为：
99．已知双曲线C：（）的左、右焦点为，，为双曲线C上一点，且，若线段与双曲线C交于另一点A，则的面积为______.
【答案】
【分析】
由已知得即，,可解得,由在双曲线C上,代入即可求得双曲线方程,然后求得直线的方程与双曲线方程联立求得点A坐标,借助,即可解得所求.
【详解】
由已知得，又，，所以，解得或，由在双曲线C上，所以或，所以或（舍去），因此双曲线C的方程为.又，所以线段的方程为，与双曲线C的方程联立消去x整理得，所以，，所以点A坐标为，所以.
100．直线：经过抛物线：（）的焦点，与抛物线相交于，两点，过原点的直线经过弦的中点，并且与抛物线交于点（异于原点），则的取值范围是______.
【答案】
【分析】
根据题意，即可求得抛物线方程；联立与抛物线方程，利用韦达定理，求得点的坐标，故可用表示；同理设出直线方程，联立抛物线方程，得到点坐标，即可将用表示，据此可将目标式转化为的函数，求函数值域即可.
【详解】
根据题意，作图如下：
因为经过抛物线：（）的焦点
故可得，则，
故可得抛物线方程为.
联立直线与抛物线方程
可得，
设，
故可得，
，
则中点坐标为，
设直线方程为，
故可得，解得，
联立直线与抛物线，
可得，解得，
即点.
则，
故可得，
又因为，故可得，
则.
故答案为：.
任务三:邪恶模式(困难)1-20题