专题8.3期末复习之选填压轴题十五大题型总结-2024-2025学年八年级数学上册举一反三系列（北师大版）

这是一份专题8.3期末复习之选填压轴题十五大题型总结-2024-2025学年八年级数学上册举一反三系列（北师大版），文件包含专题83期末复习之选填压轴题十五大题型总结北师大版原卷版docx、专题83期末复习之选填压轴题十五大题型总结北师大版解析版docx等2份试卷配套教学资源，其中试卷共89页， 欢迎下载使用。


TOC \ "1-3" \h \u
\l "_Tc26071" 【题型1 利用勾股定理求面积】 PAGEREF _Tc26071 \h 1
\l "_Tc13021" 【题型2 网格中勾股定理的运用】 PAGEREF _Tc13021 \h 7
\l "_Tc30813" 【题型3 由勾股定理求立体几何图形中的最短路径】 PAGEREF _Tc30813 \h 10
\l "_Tc20500" 【题型4 一次函数中面积有关的计算】 PAGEREF _Tc20500 \h 14
\l "_Tc1655" 【题型5 利用一次函数的性质求参数取值范围】 PAGEREF _Tc1655 \h 20
\l "_Tc18468" 【题型6 利用一次函数的性质求值】 PAGEREF _Tc18468 \h 25
\l "_Tc15435" 【题型7 动点问题的函数图象】 PAGEREF _Tc15435 \h 28
\l "_Tc15679" 【题型8 判断直角三角形】 PAGEREF _Tc15679 \h 33
\l "_Tc18266" 【题型9 勾股定理的实际应用】 PAGEREF _Tc18266 \h 38
\l "_Tc21134" 【题型10 一次函数的应用】 PAGEREF _Tc21134 \h 42
\l "_Tc792" 【题型11 平行线在翻折中的运用】 PAGEREF _Tc792 \h 46
\l "_Tc20221" 【题型12 平行线中的分类讨论思想的运用】 PAGEREF _Tc20221 \h 52
\l "_Tc5876" 【题型13 数式或图形中新定义问题】 PAGEREF _Tc5876 \h 59
\l "_Tc12173" 【题型14 数式或图形中多结论问题】 PAGEREF _Tc12173 \h 63
\l "_Tc31224" 【题型15 数式或图形中的规律探究】 PAGEREF _Tc31224 \h 69
【题型1 利用勾股定理求面积】
【例1】（2023上·陕西西安·八年级西安市铁一中学校考期末）如图，分别以Rt△ACB的直角边AB和斜边AC为边向外作正方形ABGF和正方形ACDE，连结EF．已知CB=6，EF=10，则△AEF的面积为（ ）
A．63B．83C．24D．12
【答案】D
【分析】连接CE,CF,BE,BF，设BE,CF交于点M，AC,BE交于点N，证明△ABE≌△AFC SAS，进而证明CF⊥BE，根据勾股定理得出AB2=16，AC2=52，过点A作AT⊥EF于点T，勾股定理求得AT，根据三角形的面积公式进行计算即可求解．
【详解】解：如图，
连接CE,CF,BE,BF，设BE,CF交于点M，AC,BE交于点N，
∵四边形ACDE,ABGF是正方形，
∴AC=AE,AB=AF，∠EAC=∠FAB=90°
∴∠EAC+∠CAB=∠BAF+∠CAB
即∠EAB=∠CAF，
∴△ABE≌△AFC SAS，
∴∠ACF=∠AEB，
∵∠CNE=∠CMN+∠ACF=∠NAE+∠AEB，
∴∠CMN=∠NAE=90°，
即CF⊥BE，
∴CM2+BM2=CB2,EM2+FM2=EF2，BM2+MF2=BF2,CM2+EM2=EC2，
∴CM2+BM2+EM2+FM2=CB2+EF2
∴BF2+CE2=CB2+EF2=62+102=136
又∵EC=2AC,BF=2AB，
∴2AB2+2AC2=136
又∵AC2−AB2=BC2=36，
解得：AB2=16，AC2=52，
∴AF=AB=4,AE=AC=213，
过点A作AT⊥EF于点T，
设ET=x
∴AT2=AE2−ET2=AF2−10−ET2
即52−x2=16−10−x2，
解得：x=345=6.8
∴AT=52−6.82=5.76=2.4
∴S△AEF=12×10×2.4=12，
故选：D．
【点睛】本题考查了勾股定理，全等三角形的性质与判定，证明CF⊥BE是解题的关键．
【变式1-1】（2023上·浙江金华·八年级统考期末）如图，已知长方形纸板的边长DE=10，EF=11，在纸板内部画Rt△ABC，并分别以三边为边长向外作正方形，当边HI、LM和点K、J都恰好在长方形纸板的边上时，则△ABC的面积为（ ）
A．6B．112C．254D．35
【答案】A
【分析】延长CA与GF交于点N，延长CB与EF交于点P，设AC=b，BC=a，则AB=a2+b2，证明△ABC≌△BJK≌△JKF≌△KAN，再利用长方形DEFG的面积=十个小图形的面积和进而求得ab=12，即可求解．
【详解】解：延长CA与GF交于点N，延长CB与EF交于点P，
设AC=b，BC=a，则AB=a2+b2，
∵四边形ABJK是正方形，四边形ACML是正方形，四边形BCHI是正方形，
∴AB=BJ，∠ABJ=90°，
∴∠ABC+∠PBJ=90°=∠ABC+∠BAC，
∴∠BAC=∠JBP，
∵∠ACB=∠BPJ=90°，
∴△ABC≌△BJK（AAS），
同理△ABC≌△BJK≌△JKF≌△KAN，
∴AC=BP=JF=KN=NG=b，BC=PJ=FK=AN=PE=a，
∵DE=10，EF=11，
∴2b+a=10，2a+b=11，
∴a+b=7，
∴a2+b2=49-2ab，
∵长方形DEFG的面积=十个小图形的面积和，
∴10×11=3ab+12ab×4+a2+b2+(a2+b2)2，
整理得：5ab+2(a2+b2)=110，
把a2+b2=49-2ab，代入得：5ab+2(49-2ab)=110，
∴ab=12，
∴△ABC的面积为12ab=6，
故选：A．
【点睛】本题主要考查了全等三角形的性质与判定，勾股定理，关键是构造全等三角形和直角三角形．
【变式1-2】（2023上·江苏无锡·八年级统考期末）如图，在四边形ABCD中，连接AC、BD，已知∠ADB=∠ACB=90°，∠CAB=45°，CD=2，BC=5，则四边形ABCD的面积为（ ）
A．22B．3C．72D．4
【答案】B
【分析】如图，延长BC，AD，二线交于点E，设AC，BD的交点为点M，过点C分别作CG⊥DE，垂足为G，CF⊥DB，垂足为F，证明△AGC≌△BFC即可．
【详解】如图，延长BC，AD，二线交于点E，设AC，BD的交点为点M，
∵∠ACB=∠ADB=90°，∠ADM=∠BCM，∠CAB=45°，
∴∠ACE=∠BCM=90°，∠EAC=∠MBC，AC=BC，
∴△ACE≌△BCM，
∴∠AEC=∠BMC，CM=CE，
过点C分别作CG⊥DE，垂足为G，CF⊥DB，垂足为F，
∵∠AEC=∠BMC，CM=CE，
∴△GEC≌△FMC，
∴GC=FC，
∴DC平分∠BDE，∠GDC=∠FDC=45°，四边形CGDF是正方形，
∵CD=2，
∴CG=GD=DF=FC=1，
∵BC=5，
∴BF=(5)2−1=2，
∵∠GAC=∠FBC，GC=FC，
∴△AGC≌△BFC，
∴AG=BF=2，AD=AG-DG=1，BD=BF+DF=3，
∴S四边形ABCD=12BD·CF+12BD·AD
=12BD·(DG+AD)=12BD·AG
=12×3×2=3，
故选B．
【点睛】本题考查了三角形全等的判定和性质，勾股定理，角平分线的判定定理，等腰直角三角形的判定和性质，正方形的判定和性质，熟练掌握三角形全等，勾股定理，灵活运用角的平分线的判定定理是解题的关键．
【变式1-3】（2023下·浙江宁波·八年级统考期末）如图，三角形纸片ABC，点D是BC边上一点，连接AD，把△ABD沿着AD翻折，得到△AED，DE与AC交于点G，连接BE交AD于点F．若DG＝GE，AF＝4，BF＝2，△ADG的面积为52，则点F到BC的距离为（ ）
A．55B．255C．455D．433
【答案】B
【分析】首先求出△ABD的面积．根据三角形的面积公式求出DF，设点F到BD的距离为h，根据12•BD•h＝12•BF•DF，求出BD即可解决问题．
【详解】解：∵DG＝GE，
∴S△ADG＝S△AEG＝52，
∴S△ADE＝5，
由翻折可知，△ADB≌△ADE，BE⊥AD，
∴S△ABD＝S△ADE＝5，∠BFD＝90°，
∴12•(AF+DF)•BF＝5，
∴12•(4+DF)•2＝5，
∴DF＝1，
∴DB＝BF2+DF2＝12+22＝5，
设点F到BD的距离为h，
则12•BD•h＝12•BF•DF，
即：12×5ℎ=12×2×1，
∴h＝255，
故选：B．
【点睛】本题考查翻折变换，三角形的面积，勾股定理二次根式的运算等知识，解题的关键是灵活运用所学知识解决问题，学会利用参数构建方程解决问题．
【题型2 网格中勾股定理的运用】
【例2】（2023下·安徽亳州·八年级校考期末）如图，在单位为1的正方形网格图中有a，b，c，d四条线段，从中任取三条线段所构成的三角形中恰好是直角三角形的个数为（ ）

A．0个B．1个C．2个D．3个
【答案】C
【分析】由图形和勾股定理可得a，b，c，d四条线段的长度，再根据勾股定理的逆定理，即可得到构成直角三角形的个数．
【详解】解：由图可得：a=12+12=2，b=32+32=32，c=22+22=22，d=12+32=10，
∵22+222=2+8=10=102，102+222=10+8=18=322，
∴线段a、c、d和b、c、d可以构成直角三角形，
∴从中任取三条线段所构成的三角形中恰好是直角三角形的个数为2个，
故选：C．
【点睛】本题考查了勾股定理、勾股定理逆定理，熟练掌握勾股定理以及勾股定理逆定理是解题的关键．
【变式2-1】（2023下·宁夏吴忠·八年级校考期末）如图所示的网格是正方形网格，点A，B，P是网格线的交点，则∠PAB+∠PBA=（ ）
A．30°B．45°C．60°D．75°
【答案】B
【分析】延长AP交格点于D，连接BD，根据勾股定理得PD2=BD2=5，PB2=10，求得PD2+BD2=PB2，于是得到∠PDB=90°，根据等腰直角三角形的性质和三角形外角的性质即可得到结论．
【详解】解：如图，延长AP交格点于D，连接BD，
则PD2=BD2=12+22=5，PB2=12+32=10，
∴PD2+BD2=PB2，
∴∠PDB=90°，则△DPB为等腰直角三角形，
∴∠DPB=45°，
∴∠PAB+∠PBA=∠DPB=45°，
故选：B．
【点睛】本题考查了勾股定理的逆定理，勾股定理，三角形的外角性质，等腰直角三角形的判定和性质，正确作出辅助线是解题的关键．
【变式2-2】（2023下·河北保定·八年级统考期末）如图，在每个小正方形的边长均为1的网格中，线段AB的两个端点均在格点（正方形的顶点）上．

（1）线段AB的长为 ；
（2）若△ABC是直角三角形，则网格中满足条件的格点C共有 个．
【答案】 5 6/六
【分析】（1）构造直角三角形，利用勾股定理求解即可；
（2）根据直角三角形的概念，画出图形即可得到答案．
【详解】（1）解：如图，

由勾股定理得AB=AC2+BC2=22+12=5，
故答案为：5；
（2）解：如图所示，共有6个，

故答案为：6．
【点睛】此题考查了作图-应用与设计，勾股定理，熟练掌握知识点是解题的关键．
【变式2-3】（2023下·江西新余·八年级统考期末）如图所示的网格是正方形网格，点A、B、C、D、E是网格线交点，则∠BAC−∠DAE的为 度．

【答案】45
【分析】连接CG、AG，根据勾股定理可以得出△CAG是等腰直角三角形，利用平行线性质得到∠ACF=∠BAC，从而可证△CFG≌△ADESAS，得到∠FCG=∠DAE，利用∠BAC−∠DAE=∠ACF−∠FCG求出结果即可．
【详解】解：如图，连接CG、AG，

由勾股定理得：AC2=AG2=12+22=5，CG2=12+32=10，
∴AC2+AG2=CG2，
∴∠CAG=90°，
∴△CAG是等腰直角三角形，
∴∠ACG=45°，
∴CF∥AB，
∴∠ACF=∠BAC，
在△CFG和△ADE中
CF=AD∠CFG=∠ADE=90°FG=DE
∴△CFG≌△ADESAS
∴∠FCG=∠DAE
∴∠BAC−∠DAE=∠ACF−∠FCG=∠ACG=45°，
故答案为：45．
【点睛】本题考查了勾股定理，等腰直角三角形的判定与性质，平行线的性质，全等三角形的判定与性质，正确作出辅助线利用网格线的特征是解答本题的关键．
【题型3 由勾股定理求立体几何图形中的最短路径】
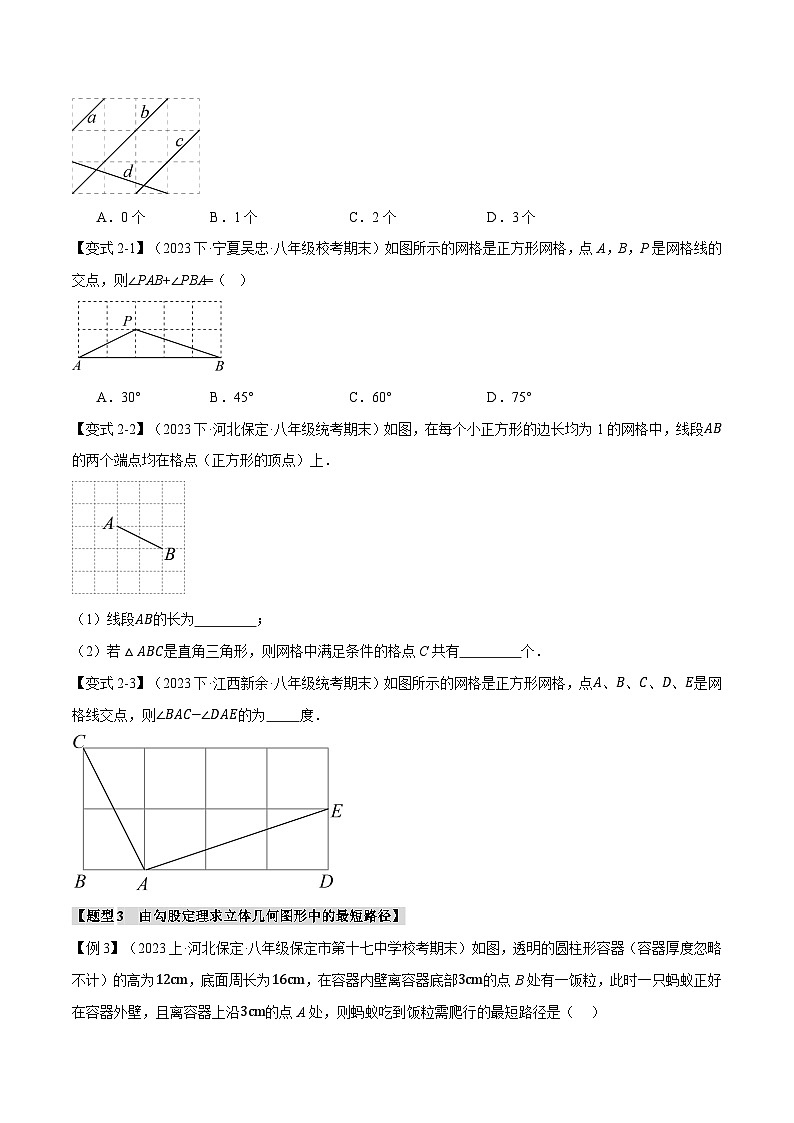
【例3】（2023上·河北保定·八年级保定市第十七中学校考期末）如图，透明的圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为16cm，在容器内壁离容器底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是（ ）
A．20cmB．413cmC．10cmD．273cm
【答案】B
【分析】根据题意，得圆柱形容器的侧面展开图为矩形MNPQ，根据矩形的性质，得MK、KB，延长AM于点A′，且AM=A′M，连接A′B，A′B交MQ于点S，连接AS，根据全等三角形的性质，通过证明△AMS≌△A′MS，得AS=A′S；根据两点之间直线段最短的性质，得蚂蚁吃到饭粒需爬行的最短路径为AS+BS，根据勾股定理的性质计算得A′B，即可得到答案．
【详解】根据题意，圆柱形容器的侧面展开图为矩形MNPQ，过点B作BH⊥NP，交NP于点H，过点B作BK⊥MN，交MN于点K；
根据题意，得：AM=3cm，MQ=NP=16cm，MN=QP=12cm，NH=PH，BH=3cm
∴NH=PH=12NP=8cm
∵BH⊥NP，BK⊥MN，∠N=90°
∴四边形KNHB为矩形
∴KB=NH=8cm，KN=BH=3cm，∠AMQ=90°
∴MK=MN−KN=12−3=9cm
如下图，延长AM于点A′，且AM=A′M，连接A′B，A′B交MQ于点S，连接AS
在△AMS和△A′MS中
A′M=AM∠A′MS=∠AMS=90°MS=MS
∴△AMS≌△A′MS
∴AS=A′S
根据题意，蚂蚁吃到饭粒需爬行的最短路径为AS+BS
∵A′M=AM
∵AM=A′M=3cm
∴A′K=A′M+MK=12cm
∴A′B=A′K2+KB2=413cm
∴AS+BS=A′S+BS=A′B=413cm，即蚂蚁吃到饭粒需爬行的最短路径是413cm
故选：B．
【点睛】本题考查了全等三角形、勾股定理、两点之间直线段最短、矩形的知识；解题的关键是熟练掌握矩形、勾股定理、两点之间直线段最短的性质，从而完成求解．
【变式3-1】（2023·八年级课时练习）如图，已知圆柱的底面直径BC=6π，高AB=3，小虫在圆柱侧面爬行，从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程的平方为（ ）
A．18B．48C．120D．72
【答案】D
【分析】要求最短路径，首先要把圆柱的侧面展开，利用两点之间线段最短，然后利用勾股定理即可求解．
【详解】解：把圆柱侧面展开，展开图如图所示，
点A，C的最短距离为线段AC的长.
∵已知圆柱的底面直径BC=6π，
∴AD=π⋅6π÷2=3，
在RtΔADC中，∠ADC=90° ，CD=AB=3，
∴AC2=AD2+CD2=18，
∴从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程的平方为2AC2=4AC2=72.
故选D.
【点睛】本题考查了平面展开-最短路径问题，解题的关键是会将圆柱的侧面展开，并利用勾股定理解答．
【变式3-2】（2023上·重庆·八年级校联考期末）如图，三级台阶，每一级的长、宽、高分别为8dm、3dm、2dm，A和B是这个台阶上两个相对的端点，点A处有一只蚂蚁，想到点B处去吃可口的食物，则蚂蚁沿着台阶面爬行到点B的最短路程为 dm．
【答案】17
【分析】先将图形平面展开，再用勾股定理根据两点之间线段最短进行解答．
【详解】解：三级台阶平面展开图为长方形，长为8dm，宽为2+3×3dm，
则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长．
可设蚂蚁沿台阶面爬行到B点最短路程为xdm，
由勾股定理得：x2=82+[2+3×3]2=172，
解得x=17．
故答案为：17．
【点睛】本题考查了平面展开−最短路径问题，用到台阶的平面展开图，只要根据题意判断出长方形的长和宽即可解答.
【变式3-3】（2023上·江苏无锡·八年级滨湖中学校考期末）棱长分别为5cm，4cm两个正方体如图放置，点P在E1F1上，且E1P=14E1F1，一只蚂蚁如果要沿着长方体的表面从点A爬到点P，需要爬行的最短距离是

【答案】106cm
【分析】根据两点之间直线最短的定理，将正方体展开即可解题.
【详解】将两个立方体平面展开，将E1F1G1B2面以E1B2为轴向上展开，连接A、P两点，得到三角形APE，AE=4+5=9，EP=4+1=5，AP=92+52=106cm.
【题型4 一次函数中面积有关的计算】
【例4】（2023上·广东深圳·八年级统考期末）如图，点A，B，C在一次函数y=−3x+b的图象上，它们的横坐标依次为-1，1，2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（ ）
A．3B．4.5C．3(b−1)D．32(b−2)
【答案】B
【详解】试题解析：将A、B、C的横坐标代入到一次函数中；
解得A（-1，b+3），B（1，b-3），C（2，b-6）．
由一次函数的性质可知，三个阴影部分三角形全等，底边长为2-1=1，高为（b-3）-（b-6）=3，
可求得阴影部分面积为：S=12×1×3×3=4.5.
故选B．
【变式4-1】（2023下·湖北武汉·八年级统考期末）在平面直角坐标系中，点A（0，4），B（-2，0），C（a，-a），△ABC的面积小于10，则a的取值范围是 ．
【答案】−143【分析】根据A、B坐标，利用待定系数法可求出直线AB的解析式，根据点C坐标可得点C在直线y=-x上，即在直线OC上，联立AB、OC解析式可得交点坐标，分a=0，a＞0，−43＜a＜0、a＜−43四种情况，画出图形，分别用a表示出△ABC的面积，根据△ABC的面积小于10列不等式求出a的取值范围即可得答案．
【详解】设直线AB的解析式为y=kx+b，
∵A（0，4），B（-2，0），
∴OA=4，OB=2，
∵点A、B在直线AB上，
∴−2k+b=0k=4，
解得：k=2b=4，
∴直线AB的解析式为y=2x+4，
①当a=0时，点C（0，0），与原点重合，
S△ABC=12OA·OB=4＜10，
∴a=0符合题意，
②如图，当a＞0时，点C（a，-a）在第四象限，连接OC，
∴S△ABC=S△ABO+S△AOC+S△BOC
=12×2×4+12×4a+12×2a
=4+3a，
∵△ABC的面积小于10，
∴4+3a＜10，
解得a＜2，
∴0＜a＜2，
∵点C（a，-a），
∴点C在直线y=-x上，即在直线OC上，
联立直线AB与直线OC的解析式得y=2x+4y=−x，
解得：x=−43y=43，
∴直线AB与直线OC的交点坐标为（−43，43），
∴a≠−43，
②如图，当−43＜a＜0时，点C在△ABO的内部，
∴S△ABC＜S△ABO＜10，
∴−43＜a＜0符合题意，
③如图，当a＜−43时，点C（a，-a）在第二象限，且在△ABO的外部，连接OC，
∴S△ABC=S△AOC+S△BOC-S△ABO
=12×4(-a)+12×2(-a)-12×2×4
=3a-4，
∵△ABC的面积小于10，
∴-3a-4＜10，
解得：a＞−143，
∴−143＜a＜−43，
综上所述：a的取值范围是−143＜a＜2，且a≠−43．
故答案为：−143＜a＜2，且a≠−43
【点睛】本题考查一次函数的交点问题及三角形的面积，熟练掌握待定系数法求一次函数解析式、利用图形正确表示出△ABC的面积并灵活运用分类讨论的思想是解题关键．
【变式4-2】（2023下·安徽芜湖·八年级校联考期末）八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这八个正方形分成面积相等的两部分，设直线l和八个正方形的最上面交点为A，则直线l的解析式是 .
【答案】y=910x
【分析】如图，利用正方形的性质得到B(0,3)，由于直线l将这八个正方形分成面积相等的两部分，则SΔAOB=5，然后根据三角形面积公式计算出AB的长，从而可得A点坐标．再由待定系数法求出直线l的解析式.
【详解】解：如图，
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分，
∴SΔAOB=4+1=5，
而OB=3，
∴ 12AB·3=5，
∴AB=103，
∴A点坐标为(103，3)．
设直线l的解析式为y=kx，
∴103k=3，解得k=910，
∴直线l的解析式为y=910x
故答案为y=910x．
【点睛】本题考查了坐标与图形性质和待定系数法求函数解析式．由割补法得SΔAOB=5求分割点A的位置是解题关键.
【变式4-3】（2023上·江苏盐城·八年级校考期末）平面直角坐标系中，O为坐标原点，直线y=13x+2与x轴交于点A，与y轴交于点B，直线y=mx+m（m≠0）将△AOB分成两部分的面积比为1:5，则m的值为 ．
【答案】2或−219
【分析】首先根据函数表达式求出A、B点的坐标，然后求出ΔAOB面积，然后根据y=mx+m的特点得知恒过点（-1，0），然后根据题意可知y=mx+m与坐标轴或y=13x+2的交点坐标，进而可求m的值；
【详解】解：由y=13x+2可知，A点坐标为（-6，0），B点坐标为（0，2）
∴SΔAOB=12·OA·OB=12×−6×2=6
∵y=mx+m=m(x+1)
∴函数恒过点（-1，0）
∵y=mx+m将ΔAOB分成的两部分面积比为1:5
∴SΔCOE=11+5SΔAOB=1或SΔACD=11+5SΔAOB=1
当SΔCOE=11+5SΔAOB=1时，
OE=2×1÷1=2
∴E点坐标为（0，2）
∴m=2，
当SΔACD=1时，
D点纵坐标为：yD=2×1÷[(−1)−(−6)]=25
∵D在y=13x+2上，
∴D点坐标为：(−245，25）
将点D的坐标代入y=mx+m,得：m=−219,
故答案为2或−219；
【点睛】本题考查了一次函数的图像，掌握并熟练使用相关知识，认真审题，精准识图，合理推论是本题的解题关键．
【题型5 利用一次函数的性质求参数取值范围】
【例5】（2023上·福建漳州·八年级校考期末）在平面直角坐标系中，一次函数y1＝m（x+3）−1（m≠0） 和y2＝a（x−1）+2（a≠0） ，无论x 取何值，始终有y2＞y1 ，m 的取值范围为（ ）
A．m≥ 34B．m> 34C．m≤ 34且m≠0 D．m< 34且m≠0
【答案】D
【分析】根据一次函数的图象和性质分别判断．
【详解】由题意可知：∵一次函数y1=mx+3−1(m≠0) 的图象过定点(−3，−1) ，
一次函数y2=ax−1+2(a≠0) 过定点(1，2) ，
∵①a<0时，m=a ，两直线平行时，始终有y2>y1 ，
∴m<0 ．
②当a>0 时，设经过点(−3，−1)，(1，2) 的直线为y3=kx+b ，有
−1=−3k+b2=k+b ，
解得： k=34b=54
∴y3= 34x+54

∵一次函数y1=mx+3−1(m≠0) 的图象过定点(−3，−1) ，
不论x 取何值，始终有y2>y1 ，
∴0∴综上解得：m<0 或0即：m< 34且m≠0
故选：D
【点睛】本题考查一次函数综合问题， 充分掌握一次函数的图象和性质是求解本题的关键．
【变式5-1】（2023下·天津红桥·八年级统考期末）关于函数y=k−3x+k（k为常数），有下列结论：①当k≠3时，此函数是一次函数；②无论k取什么值，函数图像必经过点−1,3；③若图像经过二、三、四象限，则k的取值范围是k<0；④若函数图像与x轴的交点始终在正半轴，则k的取值范围是0A．1B．2C．3D．4
【答案】D
【分析】①根据一次函数定义即可求解；②y=k−3x+k=k(x+1)−3x，即可求解；③图像经过二、三、四象限，则k−3<0，k<0，解关于k的不等式组即可；④函数图像与x轴的交点始终在正半轴，则x>0，即可求解．
【详解】解：①根据一次函数定义：形如y=kx+b(k≠0)的函数为一次函数，
∴ k−3≠0，
∴ k≠3，
故①正确；
②y=k−3x+k=k(x+1)−3x，
∴无论k取何值，函数图像必经过点−1,3，
故②正确；
③∵图像经过二、三、四象限，
∴ k−3<0k<0，
解不等式组得：k<0，
故③正确；
④令y=0，则x=−kk−3，
∵函数图像与x轴的交点始终在正半轴，
∴ −kk−3>0，
∴ kk−3<0，
经分析知：k>0k−3<0，
解这个不等式组得0故④正确．
∴①②③④都正确．
故选：D．
【点睛】本题考查了一次函数与不等式的相关知识，是难点和易错点．解答此题的关键是熟知一次函数图像上点的坐标特征，确定函数与系数之间的关系．
【变式5-2】（2023下·浙江台州·八年级统考期末）如图，Ax1,y1,Bx2,y2分别是直线y=2x+1,y=−x+4上的动点，若x1−x2≤1时，都有y1−y2≤4，则x1的取值范围为（ ）
A．−13≤x1≤0B．0≤x1≤2C．−73≤x1≤−13D．−23≤x1≤2
【答案】B
【分析】将Ax1,y1,向右平移1个单位得到点C，过点C作x的垂线，交y=−x+4于点B，交y=2x+1于点D，当BC≤4时，符合题意，同理将点A向左平移一个单位得到C，进而即可求解．
【详解】解：如图，将Ax1,y1,向右平移1个单位得到点C，过点C作x的垂线，交y=−x+4于点B，交y=2x+1于点D，当BC≤4时，符合题意，
∴Cx1+1,2x1+1，Bx1+1,−x1+1+4即Bx1+1,−x1+3，
∴BC=2x1+1−−x1+3=3x1−2
∴3x1−2≤4
解得x1≤2
如图，将点A向左平移一个单位得到C，
∴ Cx1−1，2x1+1，Bx1−1,−x1−1+4即Bx1−1,−x1+5，
∴BC=−x1+5−2x1+1 =−3x1+4 ≤4
解得x1≥0
综上所述，0≤x1≤2，
故选B
【点睛】本题考查了一次函数的性质，坐标与图形，根据题意作出图形分析是解题的关键.
【变式5-3】（2023·广西南宁·南宁市天桃实验学校校考三模）如图，在平面直角坐标系中，若折线y=−x−2+1与直线交y=kx+2k（k>0）有且仅有一个交点，则k的取值范围是（ ）
A．01或k=14C．02或k=14
【答案】B
【分析】先求出折线的最高点的坐标，然后直线经过最高点时，此时恰好有一个交点，然后分析直线与折线x<2的那部分图像的交点问题即可得到答案.
【详解】解：∵直线的解析式为y=kx+2k，
∴直线y=kx+k经过点（-2，0），
∵折线的解析式为y=−x−2+1，
∴折线的最高点坐标为（2，1）
∴当直线恰好经过（2，1）时，此时只有一个交点，
∴1=2k+2k，
解得k=14，
当k=1时，直线y=kx+2k与折线在x<2的那部分图像平行，此时没有交点，
∴当k>1时直线y=kx+2k与折线在x<2的那部分图像有一个交点，
∴综上所述k>1或k=14，
故选B.
【点睛】本题主要考查了一次函数图像的性质，解题的关键在于能够利用数形结合的思想进行求解.
【题型6 利用一次函数的性质求值】
【例6】（2023·浙江温州·温州绣山中学校考一模）如图，在平面直角坐标系中有一个3×3的正方形网格，其左下角格点A的坐标为（1，1），右上角格点B的坐标为（4，4），若分布在直线y=k(x−1)两侧的格点数相同，则k的取值可以是（ ）
A．52B．2C．74D．32
【答案】C
【分析】根据每一选项给定的k值，分别进行讨论即可得．
【详解】解：A、当k=52时，直线y=kx−1为y=52(x-1)，
当x=1时，y=0，当x=2时，y=52，当x=3时，y=5，当x=4时，y=152，此时直线左上侧有6个格点，右下侧有10个格点，故不符合题意；
B、当k=2时，直线y=kx−1为y=2(x-1)，
当x=1时，y=0，当x=2时，y=2，当x=3时，y=4，当x=4时，y=6，此时直线左上侧有6个格点，右下侧有8个格点，故不符合题意；
C、当k=74时，直线y=kx−1为y=74(x-1)，
当x=1时，y=0，当x=2时，y=74，当x=3时，y=72，当x=4时，y=214，此时直线左上侧有8个格点，右下侧有8个格点，故符合题意；
D、当k=32时，直线y=kx−1为y=32(x-1)，
当x=1时，y=0，当x=2时，y=32，当x=3时，y=3，当x=4时，y=92，此时直线左上侧有8个格点，右下侧有7个格点，故不符合题意，
故选C．
【点睛】本题考查了一次函数图象上点的坐标特征，熟知一次函数图象上的点的坐标一定满足函数的解析式是关键．
【变式6-1】（2023·四川自贡·统考中考真题）当自变量−1≤x≤3时，函数y=x−k（k为常数）的最小值为k+3，则满足条件的k的值为 ．
【答案】−2
【分析】分k<−1时，−1≤k≤3时，k>3时三种情况讨论，即可求解．
【详解】解：①若k<−1时，则当−1≤x≤3时，有x>k，故y=x−k=x−k，
故当x=−1时，y有最小值，此时函数y=−1−k，
由题意，−1−k=k+3，
解得：k=−2，满足k<−1，符合题意；
②若−1≤k≤3，则当−1≤x≤3时，y=x−k≥0，
故当x=k时，y有最小值，此时函数y=0，
由题意，0=k+3，
解得：k=−3，不满足−1≤k≤3，不符合题意；
③若k>3时，则当−1≤x≤3时，有x故当x=3时，y有最小值，此时函数y=k−3，
由题意，k−3=k+3，方程无解，此情况不存在，
综上，满足条件的k的值为−2．
故答案为：−2．
【点睛】本题考查了一次函数的性质，绝对值的性质，分类讨论是解题的关键．
【变式6-2】（2023下·宁夏银川·八年级校考期末）已知直线y=−n+1n+2x+1n+2（n为正整数）与坐标轴围成的三角形的面积为Sn，则S1+S2+S3+⋯+S2012的值为（ ）
A．5032015B．10062015C．10062014D．5032014
【答案】D
【分析】依次求出S1、S2、S3…Sn，就发现规律：Sn=12×1(n+1)(n+2)，然后求其和即可求得答案，注意1nn+1=1n−1n+1．
【详解】解：当n=1时，y=−23x+13，
此时：A（0，13 ），B（12，0），
∴S1=12×12×13=12×12×3，
当n=2时，y=−34x+14，
此时：A（0，14 ），B（13，0），
∴S2=12×13×14=12×13×4，
当n=3时，y=−45x+15，
此时：A（0，15），B（14，0），
∴S3=12×14×15=12×14×5，
……
Sn=12×1n+1×1n+2=12×1(n+1)(n+2)，
∴S1+S2+S3+…+S2012
=12×12×3+12×13×4+12×14×5+…+12×12013×2014
=12(11×2+12×3+…+12013×2014)
=1212−13+13−14+14−15+⋯+12013−12014
=1212−12014
=5032014
故选：D
【点睛】本题考查的是一次函数图象上点的坐标特点，根据题意找出规律是解答此题的关键．
【变式6-3】（2023上·山东济南·八年级统考期末）一次函数y=54x−15的图象与x轴、y轴分别交于点A、B，O为坐标原点，则在△OAB内部(包括边界)，纵坐标、横坐标都是整数的点共有（ ）
A．90个B．92个C．104个D．106个
【答案】D
【分析】求出A、B的坐标，分别求出横坐标是1、2、3、4、5、6、7、8、9、10、11的纵坐标，即可得出横坐标是1、2、3、4…时点的个数，再加上在两坐标轴上的点，即可得到答案．
【详解】解：当x＝0时，y＝﹣15，
∴B（0，﹣15），
当y＝0时，0=54x﹣15，
∴x＝12，
∴A（12，0），
x＝0时，y＝﹣15，共有16个纵坐标、横坐标都是整数的点，
x＝1时，y=54×1﹣15＝﹣1334，共有14个纵坐标、横坐标都是整数的点，
同理x＝2时，y＝﹣1212，共有13个纵坐标、横坐标都是整数的点，
x＝3时，y＝﹣1114，共有12个纵坐标、横坐标都是整数的点，
x＝4时，y＝﹣10，共有11个纵坐标、横坐标都是整数的点，
x＝5时，y＝﹣834，有9个纵坐标、横坐标都是整数的点，
x＝6时，y＝﹣712，有8个纵坐标、横坐标都是整数的点，
x＝7时，y＝﹣614，有7个纵坐标、横坐标都是整数的点
x＝8时，y＝﹣5，共有6个纵坐标、横坐标都是整数的点，
x＝9时，y＝﹣334，共有4个纵坐标、横坐标都是整数的点，
x＝10时，y＝﹣212，共有3个纵坐标、横坐标都是整数的点，
x＝11时，y＝﹣114，共有2个纵坐标、横坐标都是整数的点，
x＝12时，y＝0，共有1个即A点，纵坐标、横坐标都是整数的点．在△OAB内部（包括边界），纵坐标、横坐标都是整数的点有16+14+13+12+11+9+8+7+6+4+3+2+1＝106个．
故选：D．
【点睛】本题考查了一次函数图象上点的坐标特征的应用，通过做此题培养学生的理解能力和计算能力，本题题型较好，但是一道比较容易出错的题目．
【题型7 动点问题的函数图象】
【例7】（2023下·四川成都·八年级成都实外校考期末）如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，把线段AB以A为旋转中心，逆时针方向旋转90°，得到线段AC，设点B的横坐标为x，点C的纵坐标为y，能表示y与x的函数关系的图象大致是（ ）
A．B．
C．D．
【答案】A
【分析】作出适当的辅助线，证得ΔAOB≌ΔCDA，即可建立y与x的函数关系，确定出答案．
【详解】解：过点C作CD⊥y轴于点D，
∵∠AOB=90°，
∴∠CDA=∠AOB，∠OBA+∠OAB=90°，
∵∠CAB=90°，
∴∠CAD+∠OAB=90° ，
∴∠CAD=∠OBA，
又∵AB=AC，
∴ΔAOB≌ΔCDAAAS，
∴DA=OB=x，
∴y=OD=DA+OA=x+1，
又∵点B是x轴正半轴上的一动点，
∴x＞0，
故选：A.
【点睛】本题考查了动点问题的函数图象问题，解题的关键是明确题意，建立函数关系，从而判断出正确的函数图象．
【变式7-1】（2023下·山东潍坊·八年级统考期末）如图，在直角坐标系中，有一矩形ABCD，长AD=2，宽AB=1, AB//y轴，AD//x轴．点D坐标为3,1，该矩形边上有一动点P，沿A→B→C→D→A运动一周，则点P的纵坐标yp与点P走过的路程s之间的函数关系用图象表示大致是( )
A．B．
C．D．
【答案】D
【分析】根据则点P的纵坐标y随点P走过的路程s之间的函数关系图象可以分为4部分，当P点在AB上，当P点在BC上，当P点在CD上，点P在AD上即可得出图象．
【详解】∵矩形ABCD，长AD=2，宽AB=1,矩形边上有一动点P，沿A→B→C→D→A运动一周，
∴点P的纵坐标y随点P走过的路程s之间的函数关系图象可以分为4部分，
∴P点在AB上，此时纵坐标越来越大，最小值是1，最大值为2，
P点在BC上，此时纵坐标为定值2．
当P点在CD上，此时纵坐标越来越小，最大值是2，最小值为1，
P点在AD上，此时纵坐标为定值1．
故选：D．
【点睛】此题主要考查了动点问题的函数图象问题，解决问题的关键是分解函数得出不同位置时的函数关系，进而得出图象．
【变式7-2】（2023上·辽宁鞍山·八年级统考期末）已知点A为某封闭图形边界上一定点，动点P从点A出发，沿其边界顺时针匀速运动一周．设点P运动的时间为x，线段AP的长为y．表示y与x的函数关系的图象大致如右图所示，则该封闭图形可能是( )
A．B．C．D．
【答案】A
【详解】解：分析题中所给函数图像，
O−E段，AP随x的增大而增大，长度与点P的运动时间成正比．
E−F段，AP逐渐减小，到达最小值时又逐渐增大，排除C、D选项，
F−G段，AP逐渐减小直至为0，排除B选项．
故选A．
【点睛】本题考查了动点问题的函数图象，函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．用图象解决问题时，要理清图象的含义即会识图．
【变式7-3】（2023上·福建龙岩·八年级校考期末）如图，在平面直角坐标系中，矩形ABCD在第一象限，且AB//x轴．直线m：y=−x沿x轴正方向平移，被矩形ABCD截得的线段EF的长度L与平移的距离a之间的函数关系的大致图象可能是（ ）
B．
C．D．
【答案】B
【分析】先将直线m在平移的过程中让EF发生变化的关键位置找到，分析每一种情况下的EF随a的变化情况，逐步排除其它选项后得到正确选项．
【详解】解：如图，当直线m还没有运动到直线a的位置时，它与矩形没有交点，因此，线段EF=0，所以排除A选项；
当直线m运动到直线a和直线b之间的位置时，每向右平移1个单位，则EF就增加2个单位长，此时，它们是一次函数的关系；
当直线m运动到直线b和直线c之间的位置时，此时EF的长度始终保持不变，所以排除C选项；
当直线m运动到直线c和直线d之间的位置时，每向右平移1各单位，则EF就减少2个单位长，此时，它们是一次函数的关系，直到运动到直线d的位置时，EF的长变为0，因为从直线a的位置运动到直线b的位置和从直线c的位置运动到直线d的位置时，直线m平移的距离是相同的，因此排除D选项；
综上可得B选项正确；
故选：B．
【点睛】本题考查了一次函数的图像与性质和图形的平移等内容，解题过程中渗透了数形结合的思想，要求学生注意分析两个变量之间的关系，抓住关键的点，此题为选择题，因此可以通过排除法去排除不正确的选项，最后得到正确的选项，同时考查了学生对图形运动的感知能力与对函数图像的理解力．
【题型8 判断直角三角形】
【例8】（2023上·浙江·八年级期末）如图，∠BOC=60°，点A是BO延长线上的一点，OA=10cm，动点P从点A出发沿AB以3cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P，Q同时出发，用t(s)表示移动的时间，当t= s时，△POQ是等腰三角形；当t= s时，△POQ是直角三角形．
【答案】 52或5 4或10
【分析】根据ΔPOQ是等腰三角形，分两种情况进行讨论：点P在AO上，或点P在BO上；根据ΔPOQ是直角三角形，分两种情况进行讨论：PQ⊥AB，或PQ⊥OC，据此进行计算即可．
【详解】解：如图，当PO=QO时，ΔPOQ是等腰三角形，
∵PO=AO−AP=10−3t，OQ=t，
∴当PO=QO时，10−3t=t，
解得t=52；
如图，当PO=QO时，ΔPOQ是等腰三角形，
∵PO=AP−AO=3t−10，OQ=t，
∴当PO=QO时，3t−10=t，
解得t=5；
如图，当PQ⊥AB时，ΔPOQ是直角三角形，且QO=2OP，
∵PO=AP−AO=3t−10，OQ=t，
∴当QO=2OP时，t=2×(3t−10)，
解得t=4；
如图，当PQ⊥OC时，ΔPOQ是直角三角形，且2QO=OP，
∵PO=AP−AO=3t−10，OQ=t，
∴当2QO=OP时，2t=3t−10，
解得：t=10．
故答案为：52或5；4或10．
【点睛】本题主要考查了等腰三角形的性质以及直角三角形的性质，解决问题的关键是进行分类讨论，分类时注意不能遗漏，也不能重复．
【变式8-1】（2023上·四川·八年级校考期末）如图，在ΔABC中，AB=AC=20,BC=32，点D在线段BC上以每秒2个单位的速度从B向C移动，连接AD，当点D移动 秒时，AD与ΔABC的边垂直．
【答案】3.5或8或12.5．
【分析】设运动时间为t,然后分当AD⊥AC、AD⊥BC和AD⊥AB三种情况运用勾股定理解答即可．
【详解】解：设运动时间为t,
则BD=2t,CD=BC−BD=32−2t，
①当AD⊥AC时，如图1所示，
过点A作AH⊥BC于点H,
∵AB=AC=20,BC=32，
∴BH=CH=12BC=16,
RtΔABH中有AB2=BH2+AH2，
∴AH=AB2−BH2=12，
∴DH=BH−BD=16−2t,
RtΔADH中，AD2=AH2+DH2，
RtΔACD中，CD2=AD2+AC2，
∴CD2=AH2+DH2+AC2，
∴32−2t2=144+16−2t2+400，
解得：t=3.5；
②当AD⊥BC时，如图2所示，
由①可知，BD=12BC=12×32=16,
又BD=2t,
∴t=8；
③当AD⊥AB时，如图3所示，
过点A作AM⊥BC于点M,
由①知AM=12，
RtΔAMD中有AM2+DM2=AD2，
RtΔABD中有AB2+AD2=BD2，
∴BD2=AB2+AM2+DM2，
又BD=2t，AB=20,AM=12,DM=2t−16,
∴4t2=400+144+4t2−64t+256,
∴t=12.5
∴当D点移动3.5秒或8秒或12.5秒时，AD与ΔABC边垂直．
故答案为：3.5或8或12.5．
【点睛】本题考查了勾股定理的应用，灵活运用勾股定理列方程以及分类讨论思想是解答本题的关键．
【变式8-2】（2023上·浙江·八年级期末）如图，在△ABC中，AC=BC，CD⊥AB，CD=5，AB=24．E是AB边上的一个动点，点F与点A关于直线CE对称，当△AEF为直角三角形时，AE的长为 ．
【答案】7或17
【分析】分当E在线段AD上时，当E在线段BD上时分别求解即可．
【详解】解：当E在线段AD上时，
连接CE，作A关于CE的对称点F，连接AF，EF，CF，
∵∠AEF=90°，
∴∠AEC=∠FEC=360°−90°2=135°，
∴∠CED=45°，
∴CD=ED=5，
∴AE=AD-ED=12-5=7；
当E在线段BD上时，
连接CE，作A关于CE的对称点F，连接EF，CF，AF，
∵∠AEF=90°，
∴∠CEF=∠CEA=45°，
∴ED=CD=5，
∴AE=AD+DE=17，
故答案为：7或17．
【点睛】本题考查了等腰三角形三线合一的性质，等腰直角三角形的性质，轴对称的性质，解本题的关键是注意运用数形结合的思想解决问题．
【变式8-3】（2023下·浙江宁波·八年级统考期末）同一平面内有A，B，C三点，A，B两点之间的距离为5cm，点C到直线AB的距离为2cm，且△ABC为直角三角形，则满足上述条件的点C有 个．
【答案】8
【分析】该题存在两种情况；（1）AB为斜边，则∠C=90°；（2）AB为直角边，AC=2cm或BC=2cm；
【详解】（1）当AB为斜边时，点C到直线AB的距离为2cm，即AB边上的高为2cm，符合要求的C点有4个，如图：
（2）当AB为直角边时，AC=2cm或BC=2cm，符合条件的点有4个，如图；
符合要求的C点有8个；
故答案是8．
【点睛】本题主要考查了勾股定理的应用，准确分析判断是解题的关键．
【题型9 勾股定理的实际应用】
【例9】（2023·江西九江·校考模拟预测）我国古代数学名著《九章算术》中有这样一道题目，大致意思是：有一竖立着的木杆，在木杆的上端系有绳索，绳索从木杆上端顺着木杆下垂后，堆在地面上的部分有3尺，牵着绳索头（绳索头与地面接触）退行，在离木杆底部8尺处时，绳索用尽．问绳索长为多少．绳索长为 尺．
【答案】736
【分析】设绳索AC的长为x尺，则木柱AB的长为x−3尺，在Rt△ABC中，根据勾股定理即可列出方程解答即可．
【详解】解：设绳索AC的长为x尺，则木柱AB的长为x−3尺，
在Rt△ABC中，由勾股定理得，AC2−AB2=BC2，
即x2−x−32=82，
解得x=736，
答：绳索长为736尺．
故答案为：736．
【点睛】本题考查了勾股定理的应用，熟记直角三角形两直角边的平方和等于斜边的平方是解题的关键．
【变式9-1】（2023下·浙江绍兴·八年级统考期末）如图，斜靠在墙上的一根竹竿，AB＝10m，BC＝6m，若A端沿垂直于地面的方向AC下移2m，则B端将沿CB方向移动的距离是（ ）米．
A．1.6B．1.8C．2D．2.2
【答案】C
【分析】直接利用勾股定理得出AC的长，再利用勾股定理得出CB'，进而得出B端将沿CB方向移动．
【详解】在Rt△ABC中，∠ACB= 90°
∵AB=10，BC=6，
∴AC=AB2−BC2=102−62=8，
当AC下移2m后，A'C=8-2=6，
在Rt∆A'B'C中，∠A'CB' = 90°
B'C=A'B'2−A'C2=102−62=8，
B'C- BC=8-6= 2
∴移动了2m
故选：C.
【点睛】此题主要考查了勾股定理的应用，正确应用勾股定理是解题关键．
【变式9-2】（2023上·山东济南·八年级统考期末）如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为（ ）
A．40海里B．402海里C．80海里D．406海里
【答案】B
【分析】过点P作PC⊥AB，则在Rt△APC中，通过30°的直角三角形，计算出PC的长，再根据等腰直角三角形，通过勾股定理即可求出PB．
【详解】解：作PC⊥AB于C点，
∵A在P的北偏东30°方向，
∴∠EPA=30°，
∴∠APC=90°−∠EPA=90°−30°=60°，
又∵B在P的南偏东45°方向上，
∴∠FPB=45°，
∴∠BPC=90°−∠FPB=90°−45°=45°，
∴∠APC＝60°，∠BPC＝45°，AP＝80（海里）
∴在Rt△APC中，∠PAC=90°−∠APC=90°−60°=30°，
∴PC=12AP=12×80=40（海里）
∵在Rt△PCB中，∠BPC＝45°，
∴三角形为等腰直角三角形，
∴PC=BC=40，
∴PB=PC2+PB2=402+402=402（海里）．
故选：B．
【点睛】本题考查方位角有关的计算以及用勾股定理求航海问题，解决本题的关键是构建直角三角形进行计算．
【变式9-3】（2023上·浙江宁波·八年级统考期末）如图，一棵高5米的树AB被强台风吹斜，与地面BC形成60°夹角，之后又被超强台风在点D处吹断，点A恰好落在BC边上的点E处，若BE=2，则BD的长是（ ）
A．2B．3C．218D．247
【答案】C
【分析】过点D作DM⊥BC，设BD=x，然后根据题意和含30°的直角三角形性质分别表示出BM，EM，DE的长，结合勾股定理列方程求解．
【详解】解：过点D作DM⊥BC，设BD=x，
由题意可得：AB=5，AD=DE=5-x
∵∠ABC=60°，DM⊥BC，
∴在Rt△BDM中，∠BDM=30°
∴BM=12BD=12x，则ME=BE−BM=2−12x
∴BD2−BM2=DE2−ME2，x2−(12x)2=(5−x)2−(2−12x)2
解得：x=218，即BD=218米
故选：C．
【点睛】本题考查含30°的直角三角形性质和勾股定理解直角三角形，正确理解题意掌握相关性质定理列方程求解是关键．
【题型10 一次函数的应用】
【例10】（2023上·浙江宁波·八年级统考期末）甲开汽车，乙骑自行车从M地出发沿一条公路匀速前往N地，设乙行驶的时间为t（h），甲、乙行驶的路程分别为S甲,S乙，路程与时间的函数关系如图所示，丙与乙同时出发，从N地沿同一条公路匀速前往M地．当丙与乙相遇时，甲、乙两人相距20km，问丙出发后 小时后与甲相遇．
【答案】74或76
【分析】利用函数图象的信息求得三人的速度，再利用题意列出方程，解方程即可得出结论．
【详解】解：由函数图象得：乙的速度为80÷4＝20（km/h），
乙出发1小时后，甲出发并经过0.5小时追上乙，
设甲的速度为xkm/h，
∴20×1.5=(1.5−1)x，
∴x＝60，
∴甲的速度为60km/h．
设丙与乙相遇时乙出发了t小时，
∵当丙与乙相遇时，甲、乙两人相距20km，
∴60(t−1)−20t＝20或20t−60(t−1)=20
∴t＝2或1，
∴丙的速度为(80−2×20)÷2=20（km/h）或(80−1×20)÷1=60（km/h），
设丙出发后y小时后与甲相遇，
∴20y+60(y−1)=80，或60y+60(y−1)＝80，
解得：y＝74或76，
故答案为：74或76．
【点睛】本题主要考查了函数的图象，利用函数的图象的信息求得三人的速度，再利用题意列出方程是解题的关键．
【变式10-1】（2023上·重庆·八年级西南大学附中校考期末）小明和小李住在同一个小区，暑假期间，他们相约去缙云山某地露营；小明先出发5分钟后，小李以65米/分的速度从小区出发，小明到达相约地点后放下装备，休息了10分钟，立即按原路以另一速度返回，途中与小李相遇，随后他们一起步行到达目的地．小李与小明之间的距离y（米）与小明出发的时间x（分）之间的关系如图，则下列说法正确的是（ ）
A．小明首次到达目的地之前的速度是75米/分
B．小明首次到达目的地时，小李距离目的地还有200米
C．从小区到目的地路程为2800米
D．小明返回时的速度是33米分
【答案】C
【分析】根据图象可知，小明5分钟行走400米，可求速度，到达目的地用时35分，可求总路程，再根据小李行走时间可知小李走的路程，利用两人相向而行时，两分钟相遇可求小明返回时速度，即可得出答案．
【详解】解：A、小明首次到达目的地之前的速度是4005=80米/分，A不正确；
B、两地间的距离为：80×35＝2800（米）．
小李在小明到达目的地时行走的路程为：65×（35-30）＝1950（米）．
2800-1950=850（米），
此时，小李距目的地还有850米，B不正确；C正确；
D、850-65×10=200（米），200÷（47-45）＝100（米/分），100-65=35（米/分）．D不正确；
故选：C．
【点睛】本题考查了行程问题的数量关系的运用，一次函数的解析式的运用，点的坐标的运用，解答时认真分析函数图象的意义是关键．
【变式10-2】（2023上·全国·八年级专题练习）有一个附有进水管和出水管的容器，在单位时间内的进水量和出水量分别一定．设从某时刻开始的5分钟内只进水不出水，在随后的15分钟内既进水又出水，得到容器内水量y（升）与时间x（分）之间的函数图象如图．若20分钟后只放水不进水，这时（x≥20时）y与x之间的函数关系式是 ．
【答案】y=−3x+95；（20≤x≤3123）
【分析】先根据图象解得进水管和出水管每分钟的进水量和出水量，然后列一次函数解析式，将（20，35）代入即可解得x≥20时，y与x之间的函数关系式．
【详解】解：设5分钟内容器内水量y（升）与时间x （分）之间的函数解析式为y＝kx+b，
把（0，0）（5，20）代入y1＝kx+b，
解得k＝4，b＝0，
故5分钟内容器内水量y（升）与时间x （分）之间的函数解析式为y1＝4x （0≤x≤5）；
进水管每分钟进4L水；
设5到20分钟之间容器内水量y（升）与时间x （分）之间的函数解析式为y2＝kx+b，
把（5，20）（20，35）代入y2＝kx+b，
解得k＝1，b＝15，
故5到20分钟之间容器内水量y（升）与时间x （分）之间的函数解析式为y2＝x+15 （5≤x≤20）
可知出水管每分钟出水3L；
20分钟后只放水不进水时函数解析式为y3＝﹣3（x﹣20）+b，
将（20，35）代入y3＝﹣3（x﹣20）+b，
解得b＝35．
故当x≥20时，y与x之间的函数关系式是y＝﹣3x+95．
当y=0时，x=3123
故答案为：y＝﹣3x+95（20≤x≤3123）．
【点睛】本题主要考查了一次函数的实际应用，解答一次函数的应用问题中，要注意自变量的取值范围还必须使实际问题有意义，解答要注意数形结合思想的运用．
【变式10-3】（2023下·重庆·八年级重庆市求精中学校校考期末）在一次趣味运动会中，“抢种抢收”的比赛规则如下：全程50米的直线跑道，在起点和终点之间，每隔10米放置一个小桶，共四个，参赛者用手托着放有4个乒乓球的盘子，在从起点跑到终点的过程中，将四个乒乓球依次放入4个小桶中（放入时间忽略不计），如果中途乒乓球掉出小桶，则需要返回将乒乓球放回桶中，率先到达终点者获胜．小明和小亮同时从起点出发，以各自的速度匀速跑步前进，小明在放入第二个乒乓球后，乒乓球跳出了小桶，落在了第二个桶的旁边，且落地后不再移动，但他并未发现，继续向前跑了一段距离，被裁判员提醒后立即原速返回捡球，并迅速放回桶中（捡球时间忽略不计），为了赶超小亮，小明将速度提高了1米/秒，小明和小亮之间的距离y（米）和出发时间x（秒）之间的函数关系如图所示，则小明在掉出乒乓球后又继续跑了 米后开始返回．
【答案】6
【分析】结合图像，运用数形结合的思想，计算判断即可．
【详解】解：根据题意，得：小明捡球后，与小亮之间的距离为4米，小亮中间没有停止也没有返回，
∴小亮的速度为(10×2+4)÷4=6(米/秒)，
根据图象，小明到达终点时，小亮距离终点还有6米，即小亮已经跑了50-6=44(米)，
所用时间为44÷6=223 (s)，
∴小明从捡到球到到达终点的用时为：223-4=103 (s),
∴小明提速后的速度为(50-10×2)÷103=9(米/秒)，
∴小明提速前的速度为9-1=8(米/秒)，
∴小明在掉出乒乓球后又继续跑了(4×8-10×2)÷2=6(米)，
故答案为：6．
【点睛】本题考查了一次函数的运用，准确理解题意，正确从图像中获取解题信息是解题的关键．
【题型11 平行线在翻折中的运用】
【例11】（2023下·湖北武汉·七年级统考期末）如图，长方形纸片ABCD，点E，F分别在AB，BC边上，将纸片沿EF折叠，使点B落在边AD上的点B′处，然后再次折叠纸片使点F与点B′重合，点C落在点C′，折痕为GH，若∠C′B′D=∠AB′E+24°，则∠EFC= 度．
【答案】147
【分析】根据将纸片沿EF折叠，使点B落在边AD上的点B'处，得出∠EB′F=∠B=90°，∠BFE=∠B′FE，可得∠AB′E+∠DB′F=90°，根据四边形ABCD为长方形，得出AD∥BC，可得∠DB′F=∠B′FB=2∠EFB，可求∠AB′E=90°−∠DB′F=90°−2∠EFB，根据GH为对称轴，可得∠C′B′F=∠CFB′=180°−∠B′FB=180°−2∠EFB，可得∠C′B′D=∠C′B′F−∠FB′D=180°−2∠EFB−2∠EFB，根据∠C′B′D=∠AB′E+24°，列方程180°−2∠EFB−2∠EFB−90°−2∠EFB=24°，解方程即可．
【详解】解：∵纸片沿EF折叠，使点B落在边AD上的点B′处，
∴∠EB′F=∠B=90°，∠BFE=∠B′FE，
∴∠AB′E+∠DB′F=90°，
∵四边形ABCD为长方形，
∴AD∥BC，
∴∠DB′F=∠B′FB=2∠EFB，
∴∠AB′E=90°−∠DB′F=90°−2∠EFB，
∵再次折叠纸片使点F与点B'重合，点C落在点C′，折痕为GH，
∴四边形GHC′B′与四边形GHCF关于EG对称，
∴∠C′B′F=∠CFB′=180°−∠B′FB=180°−2∠EFB，
∵∠C′B′D=∠C′B′F−∠FB′D，
∴∠C′B′D=180°−2∠EFB−2∠EFB，
∵∠C′B′D=∠AB′E+24°，
∴∠C′B′D−∠AB′E=24°，
∴180°−2∠EFB−2∠EFB−90°−2∠EFB=24°，
∴∠EFB=33°，
∴∠EFC=180°−∠EFB=147°，
故答案为：147
【点睛】本题主要考查了折叠的性质、平行线的性质，三角形的内角和定理及其推论，恰当应用折叠的性质是解题的关键．
【变式11-1】（2023下·江苏泰州·七年级统考期末）如图，已知线段OC与直线AB的夹角∠BOC=70°，点M在OC上，点N是直线AB上的一个动点，将△OMN沿MN折叠，使点O落在点O′处，当CO′∥AB时，则∠CO′M+∠ONO′= 度．

【答案】110或70
【分析】分两种请况：当点N在射线OA上运动时；当点N在射线OB上运动时；然后分别进行计算，即可解答．
【详解】分两种请况：
当点N在射线OA上运动时，如图：

延长CO′到D，
∵∠BOC=70°，
∴∠NOC=180°−∠BOC=110°，
由折叠得：∠NO′M=∠NOM=110°，
∵CO′∥AB，
∴∠ONO′=∠DO′N，
∴∠CO′M+∠DO′N=180°−∠NO′M=70°，
∴∠CO′M+∠ONO′=70°；
当点N在射线OB上运动时，如图：

延长CO′到E，
由折叠得：∠BOC=∠NO′M=70°，
∵CO′∥AB，
∴∠ONO′=∠EO′N，
∴∠CO′M+∠EO′N=180°−∠NO′M=110°，
∴∠CO′M+∠ONO′=110°；
综上所述：当CO′∥AB时，则∠CO′M+∠ONO′=110°或70°，
故答案为：70或110．
【点睛】本题考查了平行线的性质，翻折变换（折叠问题），分两种情况讨论是解题的关键．
【变式11-2】（2023下·湖北武汉·七年级校考期末）如图，已知AB∥CD，点E，F分别在直线AB，CD上点P在AB，CD之间且在EF的左侧．若将射线EA沿EP折叠，射线FC沿FP折叠，折叠后的两条射线互相垂直，则EPF的度数为 ．
【答案】45°或135°
【分析】根据题意画出图形，然后利用平行线的性质得出∠EMF与∠AEM和∠CFM的关系，然后可得答案．
【详解】解：如图1，
过M作MN//AB，
∵AB//CD，
∴AB//CD//NM，
∴∠AEM=∠EMN，∠NMF=∠MFC，
∵∠EMF=90°，
∴∠AEM+∠CFM=90°，
同理可得∠P=∠AEP+∠CFP，
由折叠可得：∠AEP=∠PEM=12∠AEM，∠PFC=∠PFM=12∠CFM，
∴∠P=12(∠AEM+∠CFM)=45°，
如图2，
过M作MN//AB，
∵AB//CD，
∴AB//CD//NM，
∴∠AEM+∠EMN=180°，∠NMF+∠MFC=180°，
∴∠AEM+∠EMF+∠CFM=360°，
∵∠EMF=90°，
∴∠AEM+∠CFM=360°−90°=270°，
由折叠可得：∠AEP=∠PEM=12∠AEM，∠PFC=∠PFM=12∠CFM，
∴∠P=270°×12=135°，
综上所述：∠EPF的度数为45°或135°，
故答案为：45°或135°．
【点睛】本题主要考查了平行线的性质，关键是正确画出图形，分两种情况分别计算出∠EPF的度数．
【变式11-3】（2023下·浙江温州·七年级校联考期末）如图，已知长方形纸片ABCD，点E和点F分别在边AD和BC上，且∠EFC=37°，点H和点G分别是边AD和BC上的动点，现将点A，B，C，D分别沿EF，GH折叠至点N，M，P，K，若MN∥PK，则∠KHD的度数为（ ）
A．37°或143°B．74°或96°C．37°或105°D．74°或106°
【答案】D
【分析】分两种情况讨论，①当PK在AD上方时，延长MN、KH相交于点Q，根据MN∥PK，推出EN∥KQ，得到∠AEN=∠AHQ，求出∠AEN的度数，再根据∠KHD=∠AHQ即可求解；②当PK在BC下方时，延长MN、HK相交于点O，根据MN∥PK，推出EN∥HO，得到∠AEN=∠AHO，再根据∠AHO+∠KHD=180°即可求解．
【详解】解：①当PK在AD上方时，延长MN、KH相交于点Q，如图所示
∵MN∥PK
∴∠K=∠Q
∵∠K=90°
∴∠Q=90°
∵∠MNE=90°
∴∠MNE=∠Q
∴EN∥KQ
∴∠AEN=∠AHQ
∵∠EFC=37°，AD∥BC
∴∠AEF=∠EFC=37°
∵翻折
∴∠AEF=∠NEF=37°
∴∠AEN=74°
∴∠AHQ=74°
∵∠KHD=∠AHQ
∴∠KHD=74°
②当PK在BC下方时，延长MN、HK相交于点O，如图所示
∵MN∥PK
∴∠O=∠OKP=90°
∵∠MNE=90°
∴∠MNE=∠O
∴EN∥HO
∴∠AEN=∠AHO
∵∠EFC=37°，AD∥BC
∴∠AEF=∠EFC=37°
∵翻折
∴∠AEF=∠NEF=37°
∴∠AEN=74°
∴∠AHO=74°
∵∠AHO+∠KHD=180°
∴∠KHD=106°
故选D．
【点睛】本题考查了翻折、平行线的判定和性质、对顶角等知识点，分情况讨论，画出对应图形进行求解是解答本题的关键．
【题型12 平行线中的分类讨论思想的运用】
【例12】（2023下·安徽马鞍山·七年级安徽省马鞍山市第七中学校考期末）已知，如图AB平行CD，O为平面内一点，∠EOF=40°，∠BEO,∠DFO的角平分线相交于G点，则∠EGF= °

【答案】20°或160°
【分析】根据O的位置，分两种情况讨论：再分别画出图形，当O在AB，CD之间，当O不在AB，CD之间，再利用数形结合的方法解答即可．
【详解】解：如图，过O作ON∥AB，而AB∥CD，
∴AB∥ON∥CD，

∴∠BEO=∠EON，∠DFO=∠NOF，
∵∠EOF=∠EON+∠FON=40°，
∴∠BEO+∠DFO=40°，
∵∠BEO,∠DFO的角平分线相交于G点，
∴∠BEG+∠DFG=12BEO+∠DFO=20°，
过G作GH∥AB，
同理：AB∥GH∥CD，
同理可得：∠EGF=∠EGH+∠FGH=∠BFG+∠DFG=12BEO+∠DFO=20°．
如图，过O作ON∥AB，而AB∥CD，
∴ON∥AB∥CD，

∴∠NOE=∠AEO，∠CFO=∠NOF，
∵∠EOF=40°=∠FON−∠NOE，
∴∠CFO−∠AEO=40°，
∵∠BEO,∠DFO的角平分线相交于G点，
设∠BEO=2x，∠DFO=2y，
∴∠CFO=180°−2y,∠AEO=180°−2x，
∴2x−2y=40°，即x−y=20°，
过G作GH∥AB，则GH∥AB∥CD，
∴∠HGM=∠AEM=180°−x，∠HGF=∠DFG=y，
∴∠EGF=180°−x+y=180°−x−y=160°；
故答案为：20°或160°
【点睛】本题考查的是平行公理的应用，平行线的性质，角平分线的定义，清晰的分类讨论是解本题的关键．
【变式12-1】（2023下·湖北武汉·七年级武汉市武珞路中学校考期末）已知AB∥CD，∠BAD＝40°，点M在直线AD上，N为线段CD上一点，若∠MNC＝α，则∠AMN＝ ．（用含α的式子表示）
【答案】220°﹣α或α﹣140°或α﹣40°
【分析】根据平行线的性质分三种情况求解即可．
【详解】解：如图，当点M在线段AD上时，
过点M作ME∥AB，
∴∠AME＝∠BAD＝40°，
∵ME∥AB，AB∥CD，
∴ME∥CD，
∴∠EMN+∠MNC＝180°，
∵∠MNC＝α，
∴∠EMN＝180°﹣α，
∴∠AMN＝∠AME+∠EMN＝40°+（180°﹣α）＝220°﹣α；
如图，当点M在AD的延长线上时，
过点M作ME∥AB，
∴∠AME＝∠BAD＝40°，
∵ME∥AB，AB∥CD，
∴ME∥CD，
∴∠EMN+∠MNC＝180°，
∵∠MNC＝α，
∴∠EMN＝180°﹣α，
∴∠AMN＝∠AME﹣∠EMN＝40°﹣（180°﹣α）＝α﹣140°；
如图，当点M在DA的延长线上时，
过点M作ME∥AB，
∴∠AME＝∠BAD＝40°，
∵ME∥AB，AB∥CD，
∴ME∥CD，
∴∠EMN＝∠MNC＝α，
∴∠AMN＝∠EMN﹣∠AME＝α﹣40°＝α﹣40°；
故答案为：220°﹣α或α﹣140°或α﹣40°．
【点睛】此题考查了平行线的性质，熟记平行线的性质定理并会分情况讨论是解题的关键．
【变式12-2】（2023下·广东梅州·七年级统考期末）如图，AB∥CD，∠C=60°，点E是射线CD上一点，连接AE，将△AEC沿着AE翻折得△AEF，点C的对应点为点F，若∠EAF=2∠FAB，那么∠AEC= ．

【答案】40°或72°
【分析】分AF在AB上方和AF在AB下方，两种情况进行讨论，设∠BAF=x，根据平行线的性质和翻折得出角的关系，列出方程即可得出答案．
【详解】解：分两种情况：
①如图，当AF在AB上方时，

设∠BAF=x，
∵将△AEC沿着AE翻折得△AEF，∠EAF=2∠FAB，
∴∠CAE=∠EAF=2x，∠EAB=x，
∴∠CAB=∠CAE+∠EAB=3x，
∵AB∥CD，∠C=60°，
∴∠BAC+∠C=180°，∠AEC=∠EAB
∠CAB=180°−∠C=180°−60°=120°，
∴3x=120°，
解得：x=40°，
∴∠AEC=∠EAB=40°；
②如图，当AF在AB下方时，

设∠BAF=x，
∵将△AEC沿着AE翻折得△AEF，∠EAF=2∠FAB，
∴∠CAE=∠EAF=2x，∠EAB=3x，
∴∠CAB=∠CAE+∠EAB=5x，
∵AB∥CD，∠C=60°，
∴∠AEC=∠EAB，∠CAB=180°−∠C=180°−60°=120°，
∴5x=120°，
解得：x=24°，
∴∠EAB=3×24°=72°，
∴∠AEC=∠EAB=72°，
综上所述，∠AEC=40°或72°，
故答案为：40°或72°．
【点睛】本题考查了翻折变换，平行线的性质，掌握平行线的性质及分类讨论的数学思想是解决问题的关键．
【变式12-3】（2023下·重庆·七年级重庆八中校考阶段练习）如图，PQ//MN，A、B分别为直线MN、PQ上两点，且∠BAN=45°，若射线AM绕点顺时针旋转至AN后立即回转，射线BQ绕点B逆时针旋转至BP后立即回转，两射线分别绕点A、点B不停地旋转，若射线AM转动的速度是a°/秒，射线BQ转动的速度是b°/秒，且a、b满足a−5+b−12=0．若射线AM绕点A顺时针先转动18秒，射线BQ才开始绕点B逆时针旋转，在射线BQ到达BA之前，问射线AM再转动 秒时，射线AM与射线BQ互相平行．
【答案】15或22.5
【分析】先由题意得出a，b的值，再推出射线AM绕点A顺时针先转动18秒后，AM转动至AM'的位置，∠MAM'=18°×5=90°，然后分情况讨论即可．
【详解】∵a−5+b−12=0，
∴a=5，b=1，
设射线AM再转动t秒时，射线AM、射线BQ互相平行，如图，射线AM绕点A顺时针先转动18秒后，AM转动至AM'的位置，∠MAM'=18°×5=90°，分两种情况：
①当9＜t＜18时，如图，∠QBQ'=t°，∠M'AM"=5t°，
∵∠BAN=45°=∠ABQ，
∴∠ABQ'=45°-t°，∠BAM"=5t-45°，
当∠ABQ'=∠BAM"时，BQ'//AM"，
此时，45°-t°=5t-45°，
解得t=15；
②当18＜t＜27时，如图∠QBQ'=t°，∠NAM"=5t°-90°，
∵∠BAN=45°=∠ABQ，
∴∠ABQ'=45°-t°，∠BAM"=45°-（5t°-90°）=135°-5t°，
当∠ABQ'=∠BAM"时，BQ'//AM"，
此时，45°-t°=135°-5t，
解得t=22.5；
综上所述，射线AM再转动15秒或22.5秒时，射线AM射线BQ互相平行．
故答案为：15或22.5
【点睛】本题考查了非负数的性质，平行线的判定，完全平方公式，掌握知识点是解题关键．
【题型13 数式或图形中新定义问题】
【例13】（2023上·浙江宁波·八年级统考期末）定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”．如图，在平面直角坐标系xOy中，矩形OABC的边OA=3,OC=4，点M2,0，在边AB存在点P，使得ΔCMP为“智慧三角形”，则点P的坐标为： ．
【答案】3,12或3,1或3,3
【分析】由题可知，“智慧三角形”是直角三角形，因为不确定哪个角是直角，所以分情况讨论，∠CPM=90°或∠CMP=90°，设设点P(3,a)，则AP=a，BP=4-a，根据勾股定理求出CP2，MP2，CM2，根据∠CPM=90°或∠CMP=90°，可以得到这三条边的关系，解之即可.
【详解】解：由题可知，“智慧三角形”是直角三角形，∠CPM=90°或∠CMP=90°
设点P(3,a)，则AP=a，BP=4-a
①若∠CPM=90°，在Rt△BCP中，
CP2=BP2+CB2=9+(4−a)2
在Rt△MPA中，MP2=MA2+AP2=1+a2
在Rt△MCP中，CM2=MP2+CP2=9+(4−a)2+1+a2=2a2−8a+26
又∵CM2=OM2+CO2=20
∴2a2-8a+26=20
即(a-3)(a-1)=0
解得a=3或a=1
∴P(3,3)或(3,1)
②若∠CMP=90°，在Rt△BCP中
CP2=BP2+CB2=9+(4−a)2
在Rt△MPA中，MP2=MA2+AP2=1+a2
∵CM2=OM2+CO2=20
在Rt△MCP中，CM2+MP2=CP2=20+1+a2=9+(4−a)2
即a=12
∴P(3,12)
综上，P(3,12)或(3,1)或(3,3)
故答案为P(3,12)或(3,1)或(3,3).
【点睛】本题主要考查了勾股定理的应用. 解题的关键是知道“智慧三角形”指的是直角三角形.
【变式13-1】（2019下·山东临沂·八年级统考期末） 对于平面直角坐标系xOy中的点P，给出如下定义：记点P到x轴的距离为d1，到y轴的距离为d2，若d1≥d2，则称d1为点P的最大距离；若d1＜d2，则称d2为点P的最大距离．例如：点P（-3，4）到到x轴的距离为4，到y轴的距离为3，因为3＜4，所以点P的最大距离为4．若点C在直线y=-x-2上，且点C的最大距离为5，则点C的坐标是 ．
【答案】（-5，3）或（3，-5）
【分析】根据点C的“最大距离”5，可得点C的横坐标x=±5或点C的纵坐标y=±5，代入求出结果即可．
【详解】设点C的坐标x，y
∵点C的“最大距离”为5
∴x=±5或y=±5
当x=5时，y=−7
当x=−5时，y=3
当y=5时，x=−7
当y=−5时，x=3
∴点C−5，3或3，−5
故答案为：−5，3或3，−5．
【点睛】本题是阅读材料题，考查了一次函数的应用，理解新定义的信息并结合所学知识解决问题是解题关键，将距离转化为点的坐标是重点．
【变式13-2】（2017下·北京海淀·八年级人大附中校考期中）定义：对非负实数x“四舍五入”到个位的值记为fz(x)，
即：当n为非负整数时，如果n−12≤x如：fz0=fz0.48=0，fz0.64=fz1.49=1，fz4=fz3.68=4，⋯
试解决下列问题：
①fz3= ；②fz32+3= ；
③1fz12+1⋅fz22+2+1fz22+2⋅fz32+3+1fz32+3⋅fz42+4+⋯+1fz20172+2017⋅fz20182+2018= ．
【答案】 2 3 20172018/0.9995044599
【分析】①直接根据新定义，即可求解；
②根据题意，先推导出fzn2+n等于什么，再比较n2+n与n−12的大小关系，可得n−12③根据fzn2+n=n，原式可变形为11×2+12×3+13−4+⋯+12017×2018，即可求解．
【详解】解：①fz3=2；
②∵n2+n∴n2+n当n=0时，n2+n>n−12；
当n为正整数时，∵n2+n−n−122=2n−14>0，
∴n2+n>n−122，
∴n2+n>n−12，
∴：n−12∴fzn2+n=n，
∴fz32+3=3．
③∵fzn2+n=n，
∴1fz12+1⋅fz22+2+1fz22+2⋅fz32+3+1fz32+3⋅fz42+4+⋯+1fz20172+2017⋅fz20182+2018 =11×2+12×3+13−4+⋯+12017×2018
=1−12+12−13+13−14+⋯+12017−12018
=1−12018
=20172018．
故答案为①2；② 3；③ 20172018．
【点睛】解第②小题的关键是应用“完全平方公式”和“作差的方法”分别证明到当n为非负整数时，n−12【变式13-3】（2023上·四川成都·八年级校考期中）定义：在平面直角坐标系xOy中，若点P关于直线m的对称点在图形Q的内部（不包含边界），则称点P是图形Q关于直线m的“伴随点”．如图，已知A(2,2)，B(5,1)，C(3,5)，直线l：y=−x+b，若原点O是△ABC关于直线l的“伴随点”，则b的取值范围是 ．
【答案】2【分析】本题主要考查轴对称变换后点的轨迹问题，如果满足必须在△ABC的内部，那么这个对称点一定在线段BC的下方，线段AB上方，
线段AC下方，可以发现点O关于直线y=−x+b对称后的轨迹是直线y=x，并且点A(2,2)是在直线y=x上的，
只需求直线y=x与直线BC的交点即可，利用中点坐标公式，继续求此时b的值，就可以求出b的取值范围了．
【详解】解：如下图所示，点O关于直线y=−x+b的对称点O'，并且轨迹为直线y=x；
直线y=x与直线AB交点为点A，与直线BC交点为点G接下来只要求两个点的交点坐标即可，B点通过观察，直角在直线y=x上，直接求G点即可；
∵B(5,1)，C(3,5)；
设直线解析式为y=kx+b(k≠0)；
把两个点带入解析式中的得；
5k+b=13k+b=5；
解得：k=−2，b=11；
∴y=−2x+11；
在联立两条直线求交点G坐标；
y=xy=−2x+11；
解得：x=112，y=112；
∴G(112,112)；
在计算线段OG中点坐标，线段OA中点坐标，分别带入y=−x+b中；
其中线段OG中点为(1,1)，线段OA中点为(114,114)
可以求出两个b的值，b1=2，b2=112；
∴2故答案为：2
【题型14 数式或图形中多结论问题】
【例14】（2023下·广西贵港·八年级统考期末）如图，直线m，n相交于点C(1,3)，直线m交x轴于点D(−2,0)，直线n交x轴于点B(2,0)，交y轴于点A．下列四个说法：①m⊥n；②△AOB≌△DCB；③AC=BC；④直线m的函数表达式为y=33x+233．其中正确说法的个数是（ ）
A．4B．3C．2D．1
【答案】A
【分析】直接运用待定系数法求出函数解析式，再运用一次函数图象上的点的坐标的特征、全等三角形的判定求解此题．
【详解】解：设直线m的解析式为y=k1x+b1，直线n的解析式为y=k2x+b2．
由题意得，{k1+b1=3−2k1+b1=0或{k2+b2=32k2+b2=0．
∴ {k1=33b1=233，{k2=−3b2=23．
①由k1⋅k2=33×(−3)=−1得m⊥n，那么①正确．
②由D(−2,0)，点B(2,0)得OB=2，BD=4．对于直线n，当x=0，y=−3×0+23=23，那么OA=23．根据勾股定理，得AB=OA2+OB2=(23)2+22=4．
由①得，m⊥n，得∠DCB=90°，那么∠DCB=∠AOB．由∠DCB=∠AOB，∠B=∠B，DB=AB，得ΔAOB≅ΔDCB，那么②正确．
③如图，
由题得，BE=1，CE=3，那么BC=CE2+BE2=(3)2+12=2．由②得AB=4，那么AC=2，推断出AC=BC，故③正确．
④由分析知，直线m的函数表达式为y=33x+233，那么④正确．
综上，正确的有①②③④，共4个．
故选：A．
【点睛】本题考查了用待定系数法求函数解析式、一次函数图象上的点的坐标的特征、全等三角形的判定，解题的关键是熟练掌握用待定系数法求函数解析式、一次函数图象上的点的坐标的特征、全等三角形的判定．
【变式14-1】（2023下·北京·八年级人大附中校考开学考试）在数轴上有三个互不重合的点A，B，C，它们代表的实数分别为a，b，c，下列结论中
①若abc>0，则A，B，C三点中，至少有一个点在原点右侧；
②若a+b+c＝0，则A，B，C三点中，至少有一个点在原点右侧；
③若a+c＝2b，则点B为线段AC的中点；
④O为坐标原点且A，B，C均不与O重合，若OB﹣OC＝AB﹣AC，则bc>0，
所有正确结论的序号是（ ）
A．①②B．③④C．①②③D．①②③④
【答案】D
【分析】①根据乘法法则判定a，b，c至少有一个大于0，据此可解；
②根据加法法则判定a，b，c至少有一个大于0，据此可解；
③根据两点距离公式可判断；
④分情况讨论：B、C都在点O的右侧；B、C都在点O的左侧；B、C在点O的两侧且点A在点C的右侧；B、C在点O的两侧且点A在O、C之间（不与O重合）； B、C在点O的两侧且点A在O、B之间（不与O重合）； B、C在点O的两侧且点A在B右侧时；逐一画出图形进行判断，据此可解．
【详解】解：①若abc>0，则a，b，c不可能都小于0，至少有一个大于0，所以A，B，C三点中，至少有一个点在原点右侧，故①正确；
②若a+b+c＝0，因为a，b，c不能都为0，则a，b，c中至少有一个大于0，所以A，B，C三点中，至少有一个点在原点右侧，故②正确；
③若a+c＝2b，则a- b＝b- c，点B为线段AC的中点，故③正确；
④如图1, B、C都在点O的右侧,
∵OB﹣OC＝BC， AB﹣AC=BC，
∴OB﹣OC＝AB﹣AC，此时bc>0，
如图2, B、C都在点O的左侧,
∵OB﹣OC＝BC， AB﹣AC=BC，
∴OB﹣OC＝AB﹣AC，此时bc>0，
如图3, B、C在点O的两侧时，若点A在点C的右侧，
显然OB﹣OC≠AB﹣AC，
如图4, B、C在点O的两侧时，若点A在O、C之间（不与O重合），
显然OB﹣OC≠AB﹣AC，
如图5, B、C在点O的两侧时，若点A在O、B之间（不与O重合），
显然OB﹣OC≠AB﹣AC，
如图6, B、C在点O的两侧时，若点A在B右侧时，
显然OB﹣OC≠AB﹣AC，
综上所述，若OB﹣OC＝AB﹣AC，则B、C在点O的同一侧，所以b和c同号，即 bc>0，故④正确；
故选：D．
【点睛】本题考查了数轴的有关知识及实数的运算法则，掌握运算法则及数形结合思想是解题关键．
【变式14-2】（2023上·河南郑州·八年级校联考期末）疫苗接种对新冠疫情防控至关重要，接种疫苗能够对个体进行有效保护，并降低感染率、重症率和病亡率．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过a天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务．乙地80天完成接种任务，甲、乙两地的接种人数y（万人）与接种所用时间x（天）之间的关系如图所示．由题意得出下列结论：①乙地每天接种0.5万人；②a的值为40；③当甲地接种速度放缓后，y关于x的函数解析式为y=14x+1540≤x≤100；④当乙地完成接种任务时，甲地未接种疫苗的人数为10万人．其中正确结论有（ ）个．
A．1B．2C．3D．4
【答案】C
【分析】①②根据每天接种人数=总接种人数÷接种天数，即可计算答案；
③利用待定系数法求解即可得到函数解析式；
④将x=80代入解析式得出y=35，即可求出甲地未接种疫苗的人数．
【详解】解：①乙地每天接种的人数为40÷80=0.5（万人）；
②由题意可知，甲、乙两地同时以相同速度接种，甲地经过a天后接种人数达到25万人，
25−5=0.5a，解得a=40，
③设y=kx+b，将40,25，100,40代入解析式得25=40k+b40=100k+b，解得k=14b=15，
即y关于x的函数解析式为y=14x+1540≤x≤100，
④将x=80代入y=14x+15，得y=14×80+15=35，
甲地未接种疫苗的人数为40−35=5（万人）．
故选：C．
【点睛】本题考查了一次函数的应用，待定系数法求一次函数解析式，解题关键是读懂图象信息，灵活运用所学知识解决问题，属于中考常考题型．
【变式14-3】（2023下·湖北武汉·八年级统考期中）如图，E在线段BA的延长线上，∠EAD＝∠D，∠B＝∠D，EF∥HC，连FH交AD于G，∠FGA的余角比∠DGH大16°，K为线段BC上一点，连CG，使∠CKG＝∠CGK，在∠AGK内部有射线GM，GM平分∠FGC．则下列结论：①AD∥BC；②GK平分∠AGC；③GK∥CD；④∠MGK＝16°．其中正确结论的个数有（ ）
A．4个B．3个C．2个D．1个
【答案】C
【分析】根据平行线的判定定理得到AD∥BC，故①正确；由平行线的性质得到∠AGK=∠CKG，等量代换得到∠AGK=∠CGK，求得GK平分∠AGC；故②正确；根据平行线同旁内角互补得∠D+∠DCG+∠GCK=180°，再根据题目已知∠CKG＝∠CGK，得∠D+∠DCG=2∠GKC，又根据AD∥BC，得∠D+∠DCG=2∠AGK，但根据现有条件无法证明GD=GC，故③错误；设∠AGM=α，∠MGK=β，得到∠AGK=α+β，根据角平分线的性质即可得到结论．
【详解】解：∵∠EAD=∠D，∠B=∠D，
∴∠EAD=∠B，
∴AD∥BC，故①正确；
∴∠AGK=∠CKG，
∵∠CKG=∠CGK，
∴∠AGK=∠CGK，
∴GK平分∠AGC；故②正确；
∵AD∥BC，
∴∠D+∠DCG+∠GCK=180°，
∵∠CKG＝∠CGK，
∴∠D+∠DCG+180°−2∠GKC=180°，
∴∠D+∠DCG=2∠GKC，
又∵AD∥BC，
∴∠AGK=∠CKG，
∴∠D+∠DCG=2∠AGK，
要使GK∥CD，就要使∠D=∠AGK且∠D=∠DCG，
∴就要GD=GC，
但题目没给出这个条件且利用现有条件也无法证明GD=GC，
∴故③错误；
设∠AGM=α，∠MGK=β，
∴∠AGK=α+β，
∵GK平分∠AGC，
∴∠CGK=∠AGK=α+β，
∵GM平分∠FGC，
∴∠FGM=∠CGM，
∴∠FGA+∠AGM=∠MGK+∠CGK，
∴37°+α=β+α+β，
∴β=18.5°，
∴∠MGK=18.5°，故④错误，
故选：C．
【点睛】本题考查了平行线的判定和性质，角平分线的性质，对顶角性质，正确的识别图形是解题的关键．
【题型15 数式或图形中的规律探究】
【例15】（2023下·山东滨州·八年级统考期中）如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第一次从原点0运动到点P11,1，第二次运动到点P22,0，第三次运动到点P33,−2，第四次运动到点P44,0，第五运动到点P55,2，第六次运动到点P66,0，…，按这样的运动规律，点P2022的纵坐标是（ ）
A．-2B．0C．1D．2
【答案】B
【分析】先探究点的运动规律，再结合运动后的点的坐标特点，分别得出点P运动的纵坐标的规律，再根据循环规律可得答案．
【详解】解：观察图象知，动点P每运动6次为一个循环，结合运动后的点的坐标特点，可知由图象可得纵坐标每6次运动组成一个循环：1，0，-2，0，2，0；
∵2022÷6=337，
∴经过策2022次运动后，动点P的纵坐标是0．
故选：B．
【点睛】本题考查了规律型点的坐标，数形结合并从图象中发现循环规律是解题的关键．
【变式15-1】（2023上·江苏镇江·八年级校联考期中）如果正整数a、b、c满足等式a2+b2=c2，那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表，观察表中每列数的规律，可知x+y的值为（ ）
A．47B．62C．79D．98
【答案】C
【分析】依据每列数的规律，即可得到a=n2−1,b=2n,c=n2+1，进而得出x+y的值.
【详解】解：由题可得：3=22−1,4=2×2,5=22+1……
∴a=n2−1,b=n2,c=n2+1
当c=n2+1=65,n=8
∴x=63,y=16
∴x+y=79
故选：C
【点睛】本题为勾股数与数列规律综合题；观察数列，找出规律是解答本题的关键.
【变式15-2】（2021·全国·八年级专题练习）如图是一个按某种规律排列的数阵：
根据数阵排列的规律，第n（n是整数，且n≥4）行从左向右数第（n-3）个数是（用含n的代数式表示）（ ）．
A．n2−1B．n2−2C．n2−3D．n2−4
【答案】C
【分析】观察数阵排列，可发现各数的被开方数是从1开始的连续自然数，行数中的数字个数是行数的2倍，求出n-1行的数字个数，再加上从左向右的第n-3个数，就得到所求数的被开方数，再写成算术平方根的形式即可．
【详解】由图中规律知，前（n-1）行的数据个数为2+4+6+…+2（n-1）＝n（n-1），
∴第n（n是整数，且n≥4）行从左向右数第（n-3）个数的被开方数是：n（n-1）+n-3＝n2-3，
∴第n（n是整数，且n≥4）行从左向右数第（n-3）个数是：n2−3
故选：C．
【点睛】本题考查了数字规律的知识；解题的关键是熟练掌握数字规律、二次根式的性质，从而完成求解．
【变式15-3】（2023下·广西南宁·八年级统考期末）如图，在平面直角坐标系中，点A1的坐标为1,2，以点O为圆心，以OA1长为半径画弧，交直线y=12x于点B1，过点B1作B1A2∥y轴，交直线y=2x于点A2，以点O为圆心，以OA2长为半径画弧，交直线y=12x于点B2；过点B2作B2A3∥y轴，交直线y=2x于点A3，以点O为圆心，以OA3长为半径画弧，交直线y=12x于点B3；过B3点作B3A4∥y轴，交直线y=2x于点A4，以点O为圆心，以OA4长为半径画弧，交直线y=12x于点B4，…，按照如此规律进行下去，点B2023的坐标为 ．

【答案】22023,22022
【分析】根据题意可以求得点B1的坐标，点A2的坐标，点B2的坐标，然后即可发现坐标变化的规律，从而可以求得点B2023的坐标．
【详解】由题意可得，
点A1的坐标为1,2，
设点B1的坐标为a,12a，
∵OB1=OA1，
∴a2+12a2=12+22，
解得：a=2，
∴点B1的坐标为2,1，
同理可得，点A2的坐标为2,4，点B2的坐标为4,2，
点A3的坐标为4,8，点B3的坐标为8,4，
……
∴点B2023的坐标为22023,22022，
故答案为：22023,22022．
【点睛】本题考查了一次函数图象上点的坐标特征、点的坐标的变化规律以及两点之间的距离公式，解答本题的关键是明确题意，发现题目中坐标的变化规律，求出相应的点的坐标．